中值检测的迭代中值滤波算法
陈家益 董梦艺 战荫伟 曹会英 熊刚强

摘 要: 对于高密度的脉冲噪声,现有滤波算法的去噪性能并不理想,在噪声检测与噪声滤除上存在缺陷。鉴于此,提出中值检测的迭代中值滤波算法,對噪声检测和噪声滤除的方法分别进行有效的改进。算法用灰度最值进行噪声检测,再用邻域中值作进一步的检测。对于噪声像素,运用迭代的方法,用邻域中信号像素的中值取代,充分利用了前次滤波的结果。实验结果证明,相对于现有的滤波算法,所提出的算法有着更好的滤波性能,在滤除噪声的同时,很好地保持了图像的纹理边缘和细节。
关键词: 图像去噪; 噪声检测; 噪声滤除; 迭代中值滤波; 加权中值滤波; 中值检测
中图分类号: TN911.73?34; TP391 文献标识码: A 文章编号: 1004?373X(2020)07?0070?04
Iterative median filtering algorithm based on median detection
CHEN Jiayi1, DONG Mengyi2, ZHAN Yinwei3, CAO Huiying1, XIONG Gangqiang1
(1. School of Information Engineering, Guangdong Medical University, Zhanjiang 524023, China;
2. Second Clinical Medical College, Southern Medical University, Guangzhou 510515, China;
3. School of Computer Science and Technology, Guangdong University of Technology, Guangzhou 510006, China)
Abstract: The denoising performances of the existing filtering algorithms are undesirable for removing the high density impulse noise, and they have defects in noise detection and removal, so an iterative median filtering based on median detection is proposed to effectively improve the techniques of noise dection and removal. In this algorithm, the gray extreme intensity value is adopted to perform noise detection, and then the median of neighborhood is used to perform further noise detection. The signal pixels in neighborhood are used to replace the noise pixels by iterative method, in which the previous denoising result is fully taken. The experimental results show that, in comparison with the existing filtering algorithms, the proposed filtering algorithm has better filtering performance and can perfectly maintain the texture edges and details of image while removing the noises.
Keywords: image denoising; noise detection; noise filtration; iterative median filtering; weighted median filtering; median detection
0 引 言
图像在拍摄和处理的过程中,经常受到噪声的破坏,噪声会影响图像的视觉效果和图像的处理与分析,去噪非常必要。脉冲噪声是最常见的一种噪声,随机地均匀分布于图像中,脉冲噪声分为随机值脉冲噪声和固定值脉冲噪声。
随机值脉冲噪声随机地将图像的像素灰度改为介于最小灰度值与最大灰度值之间的随机值;固定值脉冲噪声随机地将图像的像素灰度改为最小灰度值或最大灰度值[1]。对于固定值脉冲噪声,均值滤波算法[2?4]会破坏图像的细节和边缘,产生模糊效果;中值滤波算法[5]属于非线性滤波,因其具有良好的去噪性能而被广泛应用于脉冲噪声的去除。
标准的中值滤波算法对噪声图像的所有像素,统一用邻域像素的中值替代,去噪处理具有盲目性,破坏了部分像素的原信息。加权中值滤波算法和中心加权中值滤波算法[6?7],根据空间距离或灰度绝对差,有选择地赋予部分像素较高的加权系数,以剔除其作为噪声像素的新灰度的概率,但其对噪声像素和信号像素不加区分的处理,破坏了信号像素的原信息。
为了对噪声与信号像素分别进行处理,仅对噪声做去噪处理,而保持信号像素不变,学者们在滤波算法中结合噪声检测,比如开关中值滤波算法[8?10],先对图像进行噪声检测,去噪处理仅针对噪声像素,信号像素保持不变。
文獻[11]提出一种基于多级中值滤波的加权滤波算法,首先做噪声检测,对于噪声像素,将滤波邻域划分为水平和垂直10个条形子邻域,将它们的加权均值作为噪声像素新的灰度,但是其加权系数的计算提高了算法的计算复杂度,且其去噪方法未必有效。文献[12]提出基于邻域的自适应中值滤波算法(Adaptive Median Filtering Algorithm Based on Window,AMF),运用混合邻域进行噪声检测,根据噪声密度运用自适应大小的邻域对噪声进行滤除,具有一定的鲁棒性,但是其去噪所用的中值为邻域中所有像素的中值,邻域中的噪声会降低去噪的准确性。文献[13]提出一种基于概率决策的滤波算法(Probabilistic Decision Based Filter to Remove Impulse Noise,PDBF),首次提出块中值的概念,旨在克服当去噪处理所用邻域的信号像素的数量为偶数时,取中间两个像素的均值作为中值的缺陷;但是算法简单地根据灰度最值检测噪声,检测的准确性不高。为了进一步提高去噪性能,文献[14]提出一种自适应开关加权中值滤波算法(Adaptive Switching Weighted Median Filter Framework for Suppressing Salt?and?pepper Noise, ASWMF),加权中值固然能提高滤波像素的相关性,但是同时也提高了算法的计算复杂度,另外,去噪仅运用3×3和5×5大小的邻域,限制了对高密度噪声的去噪性能。
为了克服现有滤波算法的不足,进一步提高去噪效果,本文提出了一种中值检测的迭代中值滤波算法(Iterative Median Filter Based on Median Detection,IMF)。实验结果证明,相对于现有算法,IMF算法具有更优的去噪性能。
1 基于灰度最值与邻域中值的噪声检测
根据现有的文献以及实验证明[15],固定值脉冲噪声的灰度取灰度的最小值和最大值。脉冲噪声的这一灰度特征,正好可以被应用于噪声检测,将噪声图像中灰度取最小和最大值的像素识别为噪声,但是,简单地根据灰度最值进行噪声检测,检测的准确性较低。因为灰度取最值的信号像素也被识别为噪声,这部分信号像素会在下一步的去噪处理中被破坏。
因此,亟需另一种方法,在基于灰度最值检测的基础上,做进一步的检测,进而将灰度取最值的信号像素与噪声区分开。
在一个像素的邻域中,信号像素具有强相关性,灰度上具有相似性,灰度差别不大;处于邻域中心的像素,可以近似地作为其他像素的对称中心;邻域中的噪声是孤立的,与信号像素不存在相关性,在灰度上往往差别很大。根据以上分析,进一步提出基于邻域中值的检测方法。
基于灰度最值检测出来的噪声像素,如果其灰度与邻域的中值相差不大,识别为信号,否则识别为噪声。具体地,预设一个阈值[T],对每一个灰度取最值的像素,如果与邻域中值的绝对差不超过[T],则将其识别为信号,否则识别为噪声。经过实验验证,噪声检测的邻域大小取7×7,阈值取[T=4]为最优值,可准确有效地检测噪声。
2 迭代中值去噪
对检测出来的噪声像素,根据邻域的像素对其原始灰度进行估测。因为噪声像素相对于信号像素的独立性,所以邻域中的噪声像素不具有参考价值;另外,噪声的局部分布不均匀会影响灰度估测的准确性,使得灰度估测值偏离原始值。因此,仅利用邻域中的信号像素作为参考值,取其中值作为噪声像素的灰度估测值,去噪效果更优。
小邻域中的像素具有强相关性,具有更好的参考性,大邻域中的像素具有弱相关性,因此,去噪所用的邻域大小会直接影响去噪性能。在噪声密度较低时,小邻域的去噪性能比大邻域更好。但是,当噪声密度较高时,小邻域中经常不存在信号像素,噪声像素的灰度无法估测,这时,必须增大邻域,以包含信号像素。
现有的算法忽略对去噪结果的有效利用,因此,本文提出了迭代的中值滤波算法。对所有的像素,用其3×3邻域内的信号像素的中值取代,如果其3×3邻域内不存在信号像素,则不处理;然后,对之前未作处理的噪声像素,用其5×5邻域内的信号像素和已经去噪处理的像素的中值取代。类似地运用于7×7邻域。
根据以上分析,本文设定最大的去噪邻域大小为7×7,如果邻域增大到7×7,其中依然没有信号像素和已经去噪处理的像素,则取5×5邻域内所有像素的中值。
3 IMF的实现流程
设[f(p)]为像素[p]的灰度,[Np(k)]表示像素[p]的大小为[k×k]的邻域,median()为取中值的函数,[R]为噪声识别矩阵,[T]为阈值,IMF的伪代码如下:
[R]=ones(size([f]))
For each [p] in [f]
If ([f(p)=]0 or [f(p)=]255) and [f(p)-median(Np(7))>T]
[R(p)=0]
Endif
Endfor
Set [k]=3, call SubPrograme
Set [k]=5, call SubPrograme
Set [k]=7, call SubPrograme
For each [p] with [R(p)]=0
[f(p)=] median([Np(5)])
End
SubPrograme
For each [p] with [R(p)=0]
If exist pixels with [R(p)=]1 in [Np(k)]
[f(p)=] the median of them
[R(p)=]1
End
End
4 实验结果与分析
实验在以下环境中进行:Intel[?] CoreTM i5?4590 CPU @ 3.30 GHz, 8 GB RAM和Matlab R2013b。将256灰度级的标准图像Lenna与医学图像Chest_XRay作为实验图像,如图1所示。
根据视觉效果、峰值信噪比(Peak Signal to Noise Ratio,PSNR)以及结构相似性指数(Structural Similarity Index,SSIM)[16],将所提出的IMF算法与部分最近提出的且去噪性能较好的算法,如AMF[12],PDBF[13]以及ASWMF[14]进行比较。
PSNR与SSIM分别定义为:
[PSNR=10×lgm×n×2552i=1mj=1n(f(i,j)-g(i,j))2] (1)
[SSIM=(2ufug+C1)(2σfg+C2)(u2f+u2g+C1)(σ2f+σ2g+C2), C1=(K1L)2, C2=(K2L)2] (2)
式中:[m]与[n]为图像的大小;[f]为原始图像;[g]为去噪图像;[uf]和[σf]分别为图像[f]的均值和标准差;[σfg]为图像[f] 与[g]的协方差;[C1]与[C2]为平衡常数;[L=]255;[K1]与[K2]分别默认取0.01和0.03。算法的PSNR与SSIM值越大,其去噪性能越好。
4.1 去噪的视觉效果
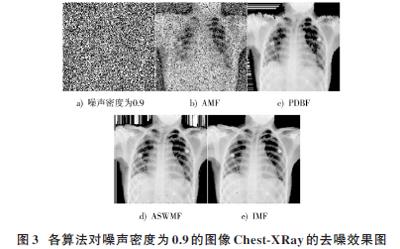
对图像Lenna和Chest_XRay分别加密度为0.8和0.9的脉冲噪声。各算法对其去噪的效果分别如图2,图3所示。对于较高密度的噪声,AMF的去噪结果会出现大片的斑点,去噪不彻底;PDBF虽然能够彻底地滤除噪声,但是其去噪图的模糊效果严重;ASWMF很好地保持了图像的边缘和细节,但是依然存在一些小斑点,纯色的背景被破坏。相对于现有的算法,IMF算法不但彻底地滤除了噪声,而且很好地保持了图像的纹理边缘和细节。
4.2 去噪的客观度量值
各算法分别对各种噪声密度的图像Lenna进行去噪,对应的PSNR和SSIM如图4所示。从图4可以看出,在噪声密度较低时,PDBF的去噪性能较差;在噪声密度较高时,AMF的去噪性能较差。相对于AMF和PDBF,ASWMF的去噪性能较好,其PSNR和SSIM曲线处于较高的位置。相对于其他算法,IMF具有更好的去噪性能,其PSNR和SSIM曲线皆处于其他算法之上。
各算法分别对各种噪声密度的图像Chest_XRay进行去噪,对应的PSNR和SSIM如图5所示。
从图5可以看出,AMF和PDBF的整体去噪性能较差;在噪声密度较低时,ASWMF的去噪性能较好,但是在噪声密度较高时,其去噪性能骤降。相对于其他算法,IMF具有更好的去噪性能,其PSNR和SSIM曲线始终处于最高,特别是在噪声密度较高时,与其他算法拉开的差距更大,优越性更加显著。
根据去噪图像的视觉效果以及去噪结果对应的PSNR和SSIM的比较分析,可以看出,相对于现有的算法,IMF算法具有更优的去噪性能,在彻底去除噪声的同时,能够很好地保持圖像的细节和纹理结构。
5 结 论
为了克服现有算法的缺陷,进一步提升去噪性能,本文提出了中值检测的迭代中值滤波算法。利用脉冲噪声的灰度最值特征以及邻域的中值进行噪声检测,较准确地对噪声进行了检测和识别。用自适应大小的邻域进行去噪,并且运用迭代的方法,充分利用了前次去噪的结果,较准确地对噪声像素的灰度进行估测。实验结果证明,相对于现有的算法,所提出的IMF算法具有更优的去噪性能,在彻底去除噪声的同时,能够很好地保持图像的细节和纹理结构。
注:本文通讯作者为战荫伟。
参考文献
[1] 陈家益,黄楠,熊刚强,等.基于灰度最值和方向纹理的概率滤波算法[J].计算机工程与应用,2017,53(8):186?192.
[2] 李智,张根耀,王蓓,等.基于中值滤波和小波变换的图像去噪[J].现代电子技术,2014,37(13):72?74.
[3] SAID A B, HADJIDJ R, MELKEMI K E, et al. Multispectral image denoising with optimized vector non?local mean filter [J]. Digital signal processing, 2016, 58: 115?126.
[4] 陈家益,曹会英,熊刚强,等.基于灰度修剪和均衡化的加权均值滤波算法[J].四川师范大学学报(自然科学版),2017,40(2):277?284.
[5] GREEN O. Efficient scalable median filtering using histogram?based operations [J]. IEEE transactions on image processing, 2017, 27(5): 2217?2228.
[6] RAMAMOORTHY K, CHELLADURAI T, SUNDARARAJAN P N. Edge analysis for noise suppression in ultrasound kidney images using weighted median filter [J]. International journal of systems signal control and engineering application, 2014, 7(2): 36?42.
[7] PARK H H. Making joint?histogram?based weighted median filter much faster [J]. Transactions on information and systems, 2015, E98(3): 721?725.
[8] ZHE Z, HAN D Q, DEZERT J, et al. A new adaptive swit?ching median filter for impulse noise reduction with pre?detection based on evidential reasoning [J]. Signal processing, 2018, 147: 173?189.
[9] MAFI M, RAJAEI H, CABRERIZO M, et al. A robust edge detection approach in the presence of high impulse noise intensity through switching adaptive median and fixed weighted mean filtering [J]. IEEE transactions on image processing, 2018, 28(11): 5475?5490.
[10] SUID M H, JUSOF M F M, AHMAD M A. Dual sliding statistics switching median filter for the removal of low level random?valued impulse noise [J]. Journal of electrical engineering and technology, 2018, 13(3): 1383?1391.
[11] 沈德海,侯建,鄂旭,等.基于改进多级中值滤波的加权滤波算法[J].现代电子技术,2015,38(12):85?88.
[12] 周萌萌,任子晖,周旋旋.基于窗口的自适应中值滤波算法[J].电视技术,2015,39(22):15?18.
[13] BALASUBRAMANIAN G, CHILAMBUCHELVAN A, VIJAYAN S, et al. Probabilistic decision based filter to remove impulse noise using patch else trimmed median [J]. AEU?International journal of electronics and communications, 2016, 70(4): 471?481.
[14] FARAGALLAHAC O S, IBRAHEMB H M. Adaptive swit?ching weighted median filter framework for suppressing salt?and?pepper noise [J]. AEU?International journal of electronics and communications, 2016, 70(8): 1034?1040.
[15] CHEN J, ZHAN Y, CAO H, et al. Adaptive probability filter for removing salt and pepper noises [J]. IET image proces?sing, 2018, 12(6): 863?871.
[16] YAO J C, LIU G Z. Improved SSIM IQA of contrast distortion based on the contrast sensitivity characteristics of HVS [J]. IET image processing, 2018, 12(6): 872?879.

