某重力坝考虑混凝土拉压损伤的地震响应分析
闫春丽,涂 劲,郭胜山
(中国水利水电科学研究院 工程抗震研究中心,北京 100048)
1 研究背景
我国是一个多地震国家,80%的水能资源集中在西部强震地区,因此保证高坝抗震安全是大坝建设中的重中之重[1]。自1967年印度Koyna重力坝在0.5g地震作用下大坝颈部出现开裂破坏以后,对强震作用下混凝土重力坝的非线性地震响应分析越来越引起人们的重视[2]。2015年颁布的能源行业标准《水电工程水工建筑物抗震设计规范》[3]规定,对于工程抗震设防为甲类,或者结构复杂或地质条件复杂的重力坝进行有限元法分析时,应考虑材料的非线性影响。但是,由于混凝土的抗拉强度通常取为其抗压强度的1/10,一般认为混凝土受拉损伤的发生先于受压损伤,因此目前很多研究在进行坝体材料动态损伤非线性分析时,主要考虑其受拉损伤[4-6],而忽略受压损伤的影响。但随着越来越多高混凝土坝的出现,尤其是在强震区坝址地震动峰值加速度越来越高的情况下,坝趾部位的静、动综合压应力数值往往超过混凝土的抗压强度,这时受压损伤是可能出现的,而进行大坝强震破坏机理及极限抗震能力研究时,考虑混凝土受压损伤是否对大坝的损伤破坏模式和极限抗震能力评价有所影响,有必要进行分析和论证。本文结合某实际重力坝工程,采用有限元软件ABAQUS,在已有的混凝土材料塑性损伤本构模型理论基础上,模拟其混凝土材料在地震荷载作用下拉压损伤、拉压转换的全过程,并通过地震超载的方式使混凝土重力坝逐步达到极限状态,探讨混凝土重力坝拉压损伤演化过程和变化趋势。
2 混凝土材料塑性损伤本构模型
本文采用有限元软件ABAQUS中[7-8]提供的混凝土塑性损伤本构模型,用于模拟混凝土等准脆性材料在循环荷载作用下的力学行为[9-12]。
2.1 损伤与刚度退化混凝土单轴受拉、受压时,塑性应变可分别表示为:


式中:dt、dc分别为受拉、受压损伤因子;E0为初始(未损伤)弹性模量;σt、σc分别为总应变所对应的拉、压应力;为受拉开裂应变;为受压非弹性应变。
混凝土单轴受拉、受压应力-应变关系可表示为:

式中:εt为拉应变;εc为压应变。
在单轴循环荷载作用下,材料的刚度退化可表示为:
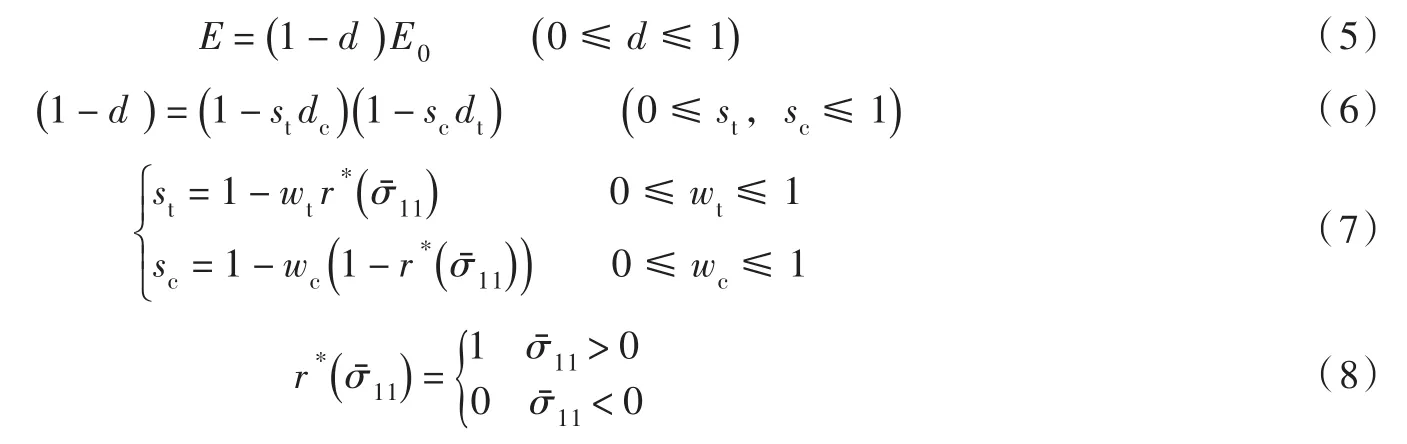
式中:E为损伤后的弹性模量;d为损伤因子;st为由受压状态进入受拉状态时的刚度恢复权函数;sc为由受拉状态进入受压状态时的刚度恢复权函数;wt、wc分别为受拉、受压刚度恢复系数,本文取ABAQUS默认值,即wc=1,wt=0。
在多轴循环荷载条件下,刚度退化机制较为复杂。假定混凝土的弹性刚度退化是各向同性的,且可以用单标量d来表示,计算中引入权重因子表征等效损伤变量,进行多轴到单轴的转换,则可进行多轴应力条件下的损伤分析。
多轴应力-应变关系可表示如下:

等效塑性应变率可通过下列式子表达:


2.2 屈服准则屈服面函数可表示如下:

其中:
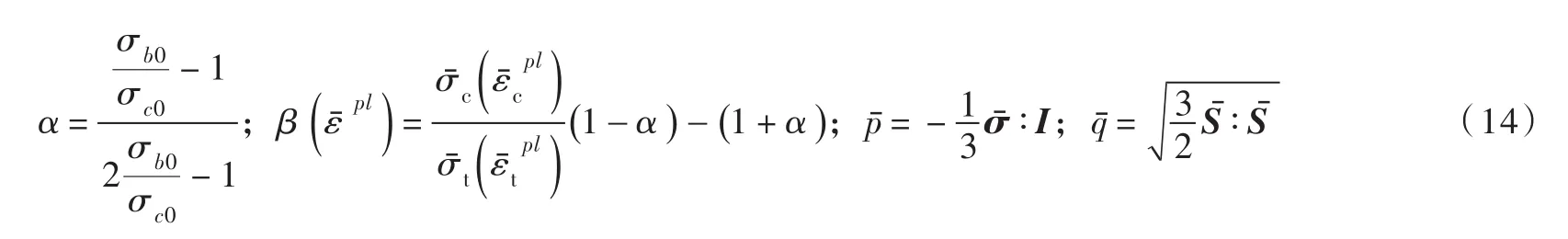
2.3 流动法则塑性损伤模型中非关联流动法则可表示如下:

流动势函数G取Drucker-Prager双曲函数形式:

式中:ψ为混凝土屈服面在强化过程中的膨胀角,由高压应力约束条件下 pˉ-qˉ关系测量获得;ϵ为离心率参数;σt0为单轴抗拉强度。本文参考《Abaqus Example Problems Guide》给出的混凝土重力坝算例中参数的取值,取ϵ=0,ψ=36.31°。
2.4 本构模型小结在循环荷载的作用下,计算中通过应力状态是否超过式(13)屈服面函数来判断混凝土是否进入塑性状态,当材料开始进入塑性状态,通过流动法则式(14)计算其塑性应变增量张量,再进行多轴到单轴的转化后得到等效拉、压塑性应变,并确定损伤因子来反映刚度退化,采用式(9)模拟损伤后的应力应变关系。
3 计算条件及计算模型
本文以某混凝土重力坝为算例,采用上述建议的混凝土塑性损伤模型,通过地震超载的方式使混凝土重力坝逐步达到极限状态[13],探讨混凝土重力坝拉压损伤演化过程和变化趋势,重点研究考虑混凝土受压损伤对重力坝极限抗震能力分析的影响。
某混凝土重力坝坝高185 m,坝顶宽度为16 m,坝底宽度为165.5 m。地基模拟范围沿深度方向和上、下游方向均取2倍坝高;坝体单元尺寸在2 m左右,坝体-地基系统总节点数7135,单元数6988。计算模型以黏弹性人工边界模拟无限地基辐射阻尼作用。
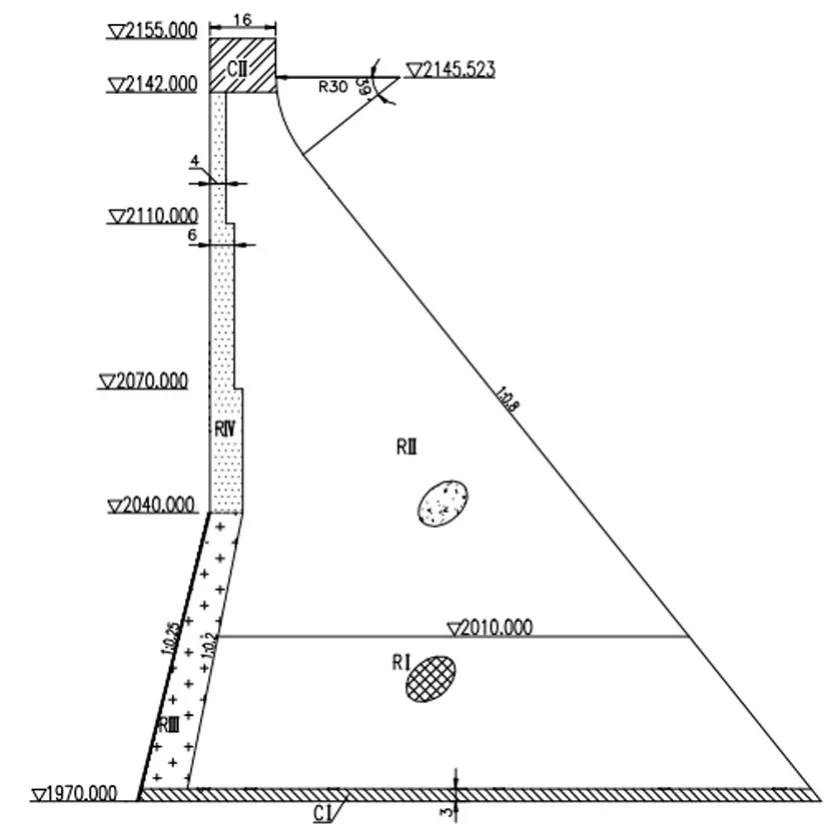
图1 非溢流坝段剖面及混凝土分区(单位:m)
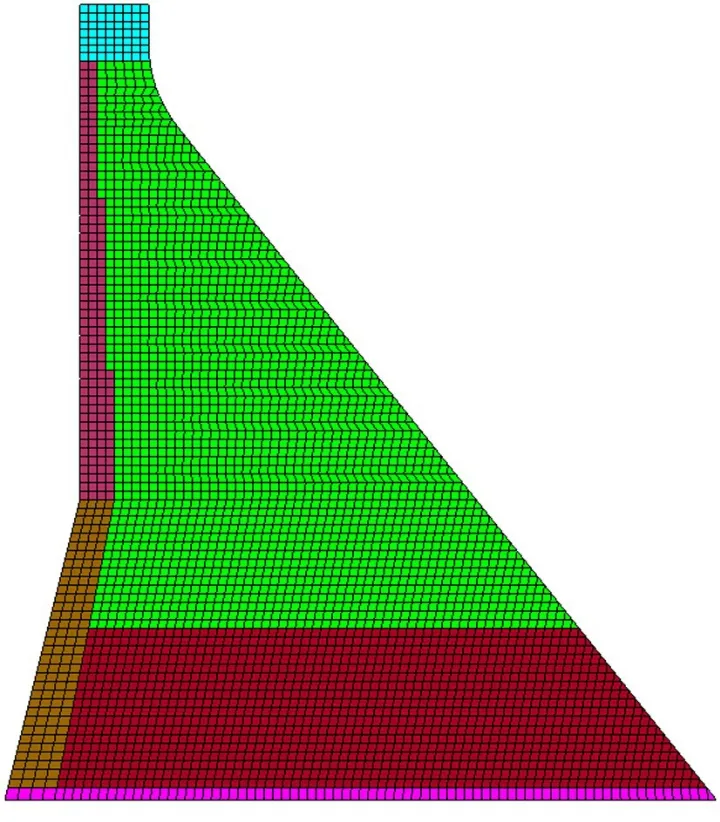
图2 坝体有限元模型
建基面高程1970.0 m,坝顶高程2155.0 m,上游正常蓄水位2150.0 m,下游水位2019.25 m,淤沙高程2023.7 m,淤沙浮容重8 kN/m3,淤砂内摩擦角12°,混凝土容重24 kN/m3,水的容重9.8 kN/m3,岩石的密度2777kg/m3。计算所用的混凝土及岩体材料的物理参数如图1和表1所示[14]。坝体的有限元单元网格尺寸约2 m,如图2所示。
作用于大坝的各项静力荷载包括有上下游静水压力、自重、淤沙压力。库水的动态影响按Westergaard附加质量法计入。计算采用的大坝设计地震水平向峰值加速度为0.4005g,图3为归一化的地震波加速度时程曲线。图4—图7为大坝混凝土损伤演化规律曲线,其受拉损伤演化规律曲线相关数据参考沙牌大坝碾压混凝土芯样试件的试验成果确定。受压损伤演化规律曲线参考文献[9]中CDP模型参数,并进行相应的折算,然后根据式(2)进行适当的调整所得。
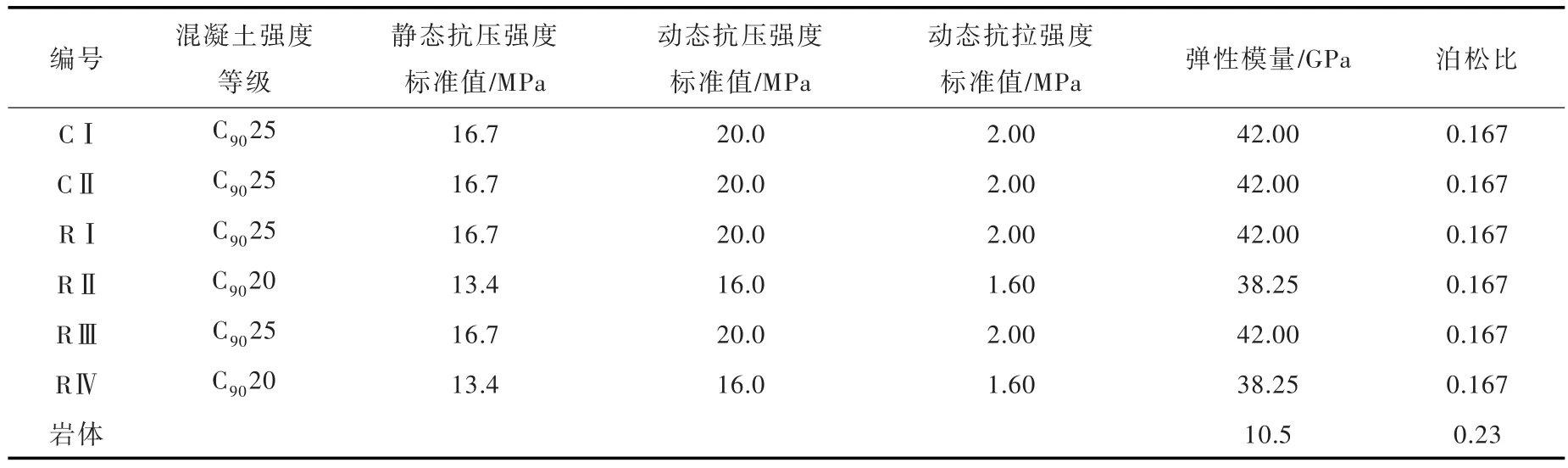
表1 混凝土和岩体的力学参数

图3 地震波加速度时程曲线
4 计算结果分析
4.1 只考虑受拉损伤计算结果图8为只考虑受拉损伤条件下在不同超载系数下裂隙的扩展情况。从图8可以看出,在设计地震时坝踵和上游面折坡处出现损伤,坝踵处损伤因子大于0.8的宏观开裂深度约为27.7 m。1.1倍超载时下游面折坡处也出现开裂,随着超载系数的不断加大,下游面折坡处的损伤逐渐向上游面扩展,到1.15倍超载时形成上下游贯通的宏观裂缝。
4.2 同时考虑拉压损伤计算结果图9为同时考虑拉压损伤条件下受拉损伤在不同超载系数下裂隙的扩展情况。由图9可以看出,同时考虑拉压损伤时,也在1.15倍超载时形成上下游贯通的宏观裂缝。因此,同时考虑拉压损伤和只考虑受拉损伤的极限抗震能力相同。
图10为同时考虑拉压损伤条件下受压损伤在不同超载系数下的扩展情况。从图10可以看出,在超载系数较小的情况下,受压损伤主要发生在坝踵,之后上、下游折坡处也出现损伤并逐渐扩展,随着超载系数不断增加,坝趾处也开始出现损伤。坝踵出现受拉损伤的部位同时也出现了受压损伤,分析其原因为,坝踵发生损伤部位采用的是C9025混凝土,在单轴状态下C9025混凝土的受压初始屈服应力为14.8 MPa(图5)。

图4 C9025大坝混凝土动态受拉损伤演化规律曲线
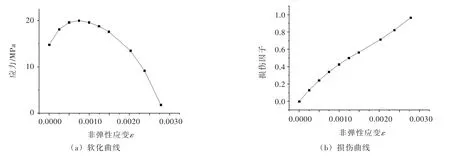
图5 C9025大坝混凝土动态受压损伤演化规律曲线
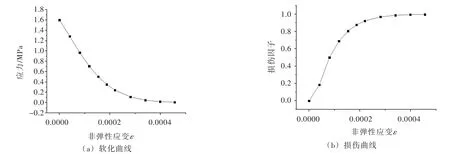
图6 C9020大坝混凝土动态受拉损伤演化规律曲线
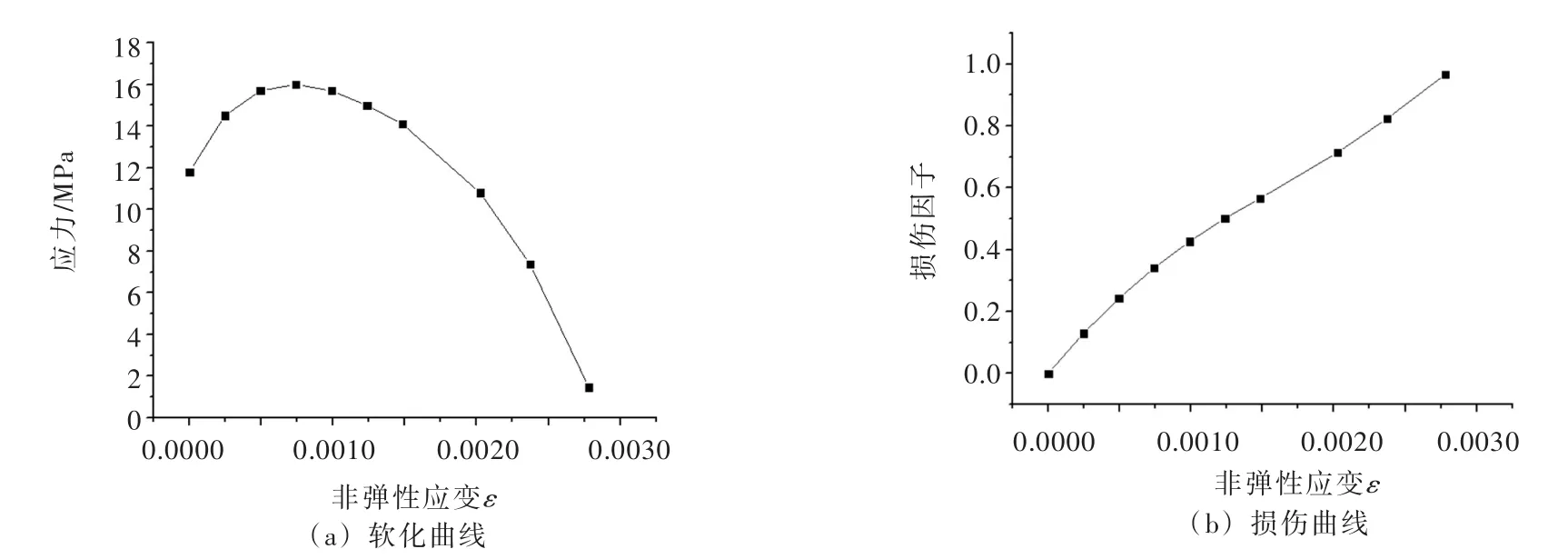
图7 C9020大坝混凝土动态受压损伤演化规律曲线
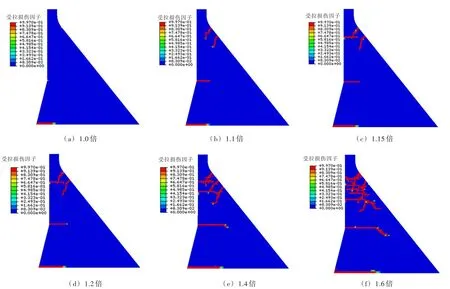
图8 只考虑受拉损伤条件下的裂缝扩展情况

图9 同时考虑拉压损伤的受拉损伤分布
以超载系数1.0的计算结果为例,从图11中可以看出受压损伤发生在7.80179 s,从表2计算结果来看,在损伤发生时坝踵附近的最大压应力并没有超过受压初始屈服应力,但是此时该高斯点处的最大主应力为1.91397 MPa,最小主应力值为-1.04945 MPa,由式(13)可求得屈服面函数F=3.7346>0,超出屈服面,依据流动法则可计算其塑性应变张量为{6.37314×10-8,- 3.06917×10-8}T,由于处在双轴拉压状态,用式(12)计算可得到权重因子为0.6459,再由式(10)和式(11)计算得到拉、压等效塑性应变分别为4.22082×10-8和1.03651×10-8,最后可求得拉、压损伤因子分别为7.09415×10-4和7.36175×10-6。因此,受压损伤因子不为0。同理,随着超载系数的增加,上、下游折坡处受拉损伤部位也产生了受压损伤。
同时,从图10中可以看到,坝趾处的受压损伤随地震超载倍数增加扩展很小。由混凝土单轴受压损伤应力-应变演化规律可以得出,当应力值超过初始屈服应力以后开始出现损伤,进入强化段,当应力值超过极限应力以后进入软化段,材料的承载能力下降,损伤进入快速扩展阶段。因此,由图12(本文采用的混凝土受压应力-应变曲线)可以看出,单轴状态下在压应变为1.218×10-3时到达极限应力,此时所对应的损伤因子为0.3412,由式(2)可求得对应的塑性应变为4.95×10-4。本文的模型坝趾部位的受压损伤是在双轴受压状态下出现的,从表3的计算结果来看,即使在1.6倍超载时,坝趾附近积分点处在时程内的最大压应变和等效塑性应变值都小于受压极限状态的对应值,时程内的最大受压损伤因子也小于极限压应力时所对应的受压损伤因子值,因此,坝趾处的混凝土材料还处在强化阶段,承载能力并未降低,所以损伤扩展很小。

表2 超载系数为1.0时在7.80179s时坝踵积分点处相关变量
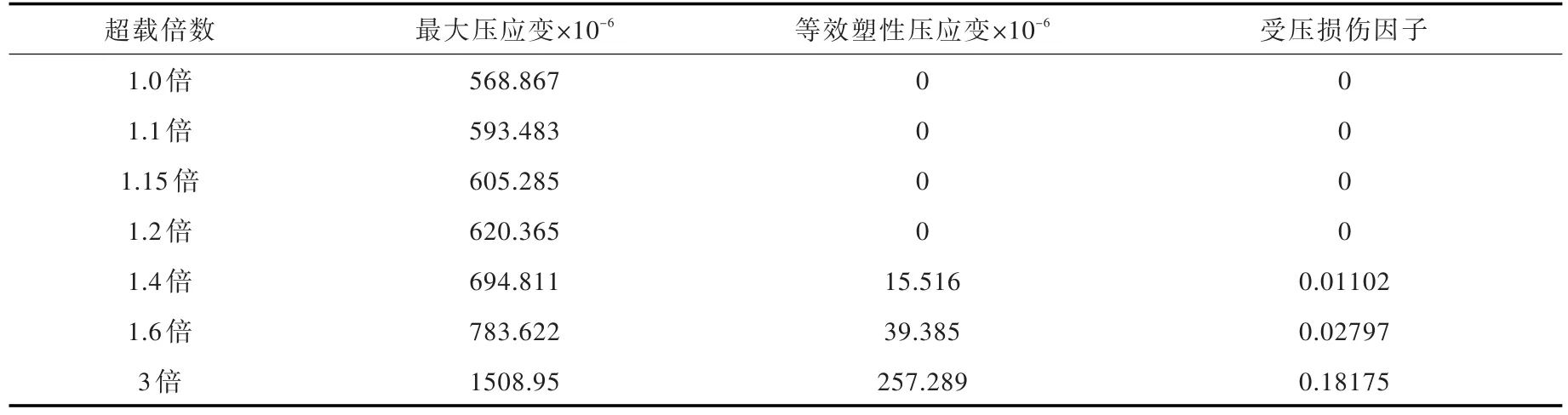
表3 坝趾积分点处在不同超载系数下的时程内最大相关变量值

图10 同时考虑拉压损伤的受压损伤分布

图11 超载系数为1.0时坝踵积分点处的受压损伤时程曲线
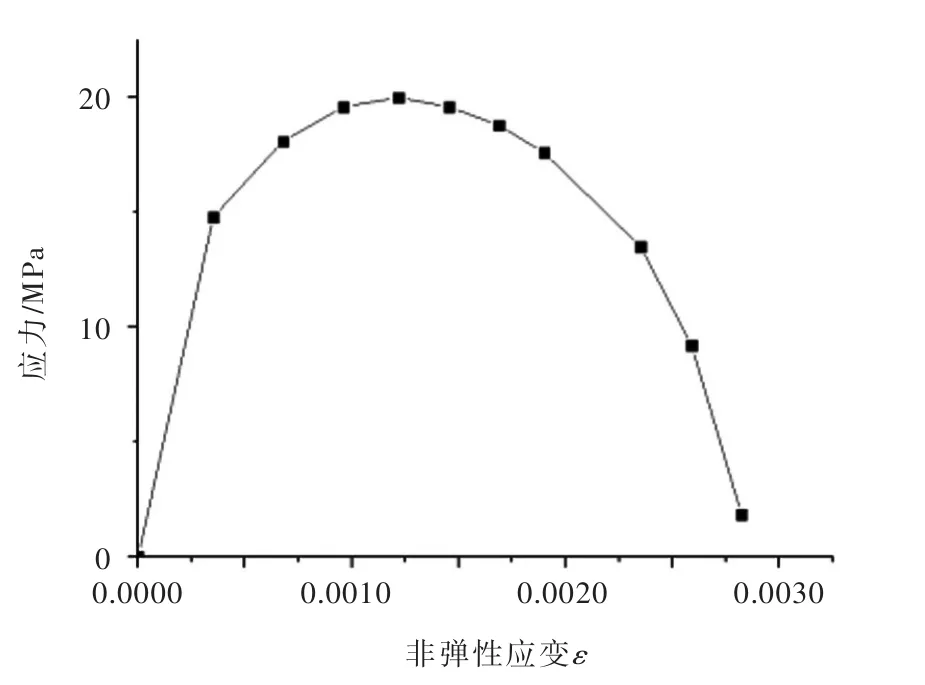
图12 C9025混凝土受压应力-应变曲线

图13 同时考虑拉压损伤的3倍超载时受压损伤分布
如图13所示,当3倍超载时,坝趾附近积分点处在时程内的最大压应变为1.50895×10-3,超过单轴状态受压极限应力对应的压应变。时程内最大等效塑性应变为2.57289×10-4,时程内最大的受压损伤因子为0.18175,仍未超过受压极限应力所对应的值,但相比1.6倍超载时,坝趾处的受压损伤区有所扩展,但范围仍有限。由此可见,重力坝在强震作用下其坝趾压应力集中区虽可能进入受压损伤状态,但由于混凝土的受压本构关系不同于受拉时的准脆性特征,体现出一定的具有强化性质的延性材料特点,在其压应变在达到进入软化段的数值之前,坝体其他部位的受拉损伤已经发展到相当严重的程度,由此看来,重力坝坝体的强震损伤极限状态还是由受拉损伤控制的。
4.3 比较分析基于上述计算结果,以大坝头部受拉损伤是否贯穿为依据,同时考虑拉压损伤的极限抗震能力和只考虑受拉损伤时的极限抗震能力相同,均为在1.1倍超载时大坝头部没有贯通,在1.15倍超载时贯通,因此大坝的极限抗震能力可取为设计地震的1.1倍。由此看来,是否同时考虑拉压损伤对重力坝极限抗震能力的判断影响不大,虽然损伤的发展形态在局部略有差异,但最终头部受拉损伤贯通的超载倍数相同。
5 结论
本文建立了考虑混凝土拉压损伤的重力坝-地基有限元模型,采用地震超载的方式开展了某重力坝在混凝土拉、压损伤的出现和发展规律以及其极限抗震承载能力的研究,其结论为:(1)同时考虑拉压损伤时,受拉损伤部位也有可能产生受压损伤,即双轴拉压状态下,拉、压损伤可能同时出现。(2)重力坝在强震作用下其坝趾压应力集中区虽可能进入受压损伤状态,但由于混凝土的受压本构关系体现出一定的具有强化性质的延性材料特点,在其受压区压应变达到进入软化段的数值之前,坝体其他部位的受拉损伤已经发展到相当严重的程度,由此看来,重力坝坝体的强震损伤极限状态主要是由受拉损伤控制的。(3)以头部损伤贯穿为判据,同时考虑拉压损伤的极限抗震能力和只考虑受拉损伤时的极限抗震能力基本相同。

