光栅光谱衍射效率测量新技术的误差分析与校正方法研究
王圣浩,邵建达,,刘世杰*,李灵巧*,吴周令,陈 坚,黄 明
1.中国科学院上海光学精密机械研究所精密光学制造与检测中心,上海 201800 2.合肥知常光电科技有限公司,安徽 合肥 230031 3.超光滑表面无损检测安徽省重点实验室,安徽 合肥 230031
引 言
衍射光栅是非常重要的色散元件,在光谱分析、强激光、光学测量以及其他领域中有着广泛的应用[1-3]。其光谱衍射效率的测量对于优化光栅制造工艺和评估光栅性能有着重要的作用[4-6],光栅光谱衍射效率的定义如式(1)
(1)
式(1)中,η(λi)为当入射单色光束的波长为λi时,光栅在m衍射级次处的衍射效率,其中I0(λi)和Im(λi)分别表示入射单色光束的强度和m衍射级次处衍射光束的强度。通过依次测量波长为λ1,λ2,…,λn-1和λn时光栅的衍射效率,即可获得λ1—λn波段范围内光栅的光谱衍射效率。
在过去的半个世纪里,研究人员提出并发展了一系列测量光栅光谱衍射效率的方法[6-8]。在2006年,为了测量具备超高衍射效率值(>99%)的反射光栅,Bunkowski提出了基于光学谐振腔的测量方法。2016年,中国科学院长春光学精密机械与物理研究所报道了基于傅里叶光学原理的衍射效率测量方法,该方法可以提高光栅光谱衍射效率的测量精度和测量效率[10]。
如图1所示是目前测量光栅光谱衍射效率比较常见的装置和方法[7-8],系统是建立在双光路光度测量结构上的,系统的主要机械组件包括转台-Ⅰ、转台-Ⅱ和固定在转台-Ⅱ上的机械臂。在测量过程中,首先旋转转台-Ⅰ使激光以α的入射角照射在待测光栅上;接着将光栅单色器出射光束的波长设置为λ1(通过调节光栅单色器内部的机械组件完成);然后根据式(2),通过转台-Ⅱ和机械臂将探测器-Ⅱ转动到待测衍射光束出射的方向(用β表示),式(2)中的d表示光栅常数;接着同时采集探测器-Ⅰ和探测器-Ⅱ获得的信号,并结合参考信号(光路中不含待测光栅时探测器-Ⅰ和探测器-Ⅱ读取的信号)计算波长为λ1时待测光栅的衍射效率η(λ1)。
d×(sinα+sinβ)=mλ
(2)
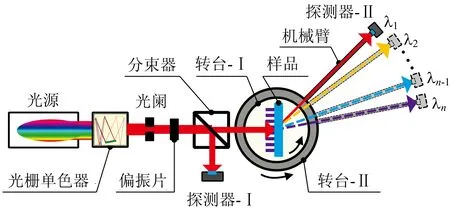
图1 目前常见的光栅光谱衍射效率的测量装置图Fig.1 Framework of the system for measuring the spectral diffraction efficiencies of a plane reflection grating using the currently popular method
接下来,将光栅单色器的输出波长依次设置为λ2,λ3,…,λn,并分别在各个波长位置处重复上述步骤以得到各个波长处的衍射效率η(λ2),η(λ3),…,η(λn),最后即可得到λ1—λn波段范围内待测光栅的光谱衍射效率。需要注意的是,从式(2)可以看出,在上述测量过程中,每次当改变波长的时候,探测器-Ⅱ的位置需要做出相应的机械移动。
该光栅光谱衍射效率测量方法具有测量精度高的优点,但是其主要缺点是测试速度比较缓慢,因为在测量过程中存在两种需要重复数百次的机械运动(一种是光栅单色器内部机械组件的运动,另一种是转台-Ⅱ的机械旋转)。事实上,只有在机械组件运动停止并稳定后才能采集数据,因此,由于数百次机械运动的存在,要测得一定波段范围内光栅的光谱衍射效率,需要较长的时间。例如,测量700~900 nm波段范围内脉冲压缩光栅的光谱衍射效率(波长间隔为1 nm),大约需要5~8 min的时间[7]。
测试速度慢的缺点阻碍了该技术的广泛应用,尤其是在需要快速完成测量的环境中,比如:(1)在光栅制造加工过程中,散射测量术(实质上是测量光栅的光谱衍射效率)广泛应用于光栅结构参数的反演[10]。早期,该技术主要是通过高速测量单个波长位置处的衍射效率以实时监控光栅加工的参数,如SiO2和Si3N4的腐蚀速率、掩膜上的线宽。后来,结合严格耦合波分析,这种简单的测量技术成为了非常有力的原位表征工具[11]。然而在一些复杂的测量环境中,为了进行快速、强健的数据重建,需要快速获得大量的衍射效率数据[10]。多个波长位置处光谱衍射效率的快速测量技术因而得到了发展,但是从式(2)可以看出,测量不同波长位置处的衍射效率是非常麻烦并且非常耗时的。因此,在大多数情况下,只能通过光谱仪高速测量零衍射级(即镜面反射方向)处的光谱衍射效率[12-13]。但是考虑到零衍射级处的衍射效率一般没有非零衍射级次处的衍射效率对光栅结构参数敏感,因此如果能在短时间内同时测量多个波长位置处(不是零衍射级)的光谱衍射效率,就可以反演计算得到光栅更多的结构参数,或者某个结构参数的反演将更加准确和强健[10]。(2)在衍射光栅的实际应用中,温度和湿度等环境参数对光栅的微观结构有着不可忽视的影响,从而影响了光栅的光谱衍射效率[14]。因此,在诸如环境温度变化情况下,测量光栅光谱衍射效率的动态变化情况,将为不同环境下准确使用光栅提供充足的数据支持。(3)在大规模工业生产中,需要快速测量光栅的光谱衍射效率,以提高生产效率。
1 新方法的测量原理
在之前的研究中,我们报道了一种快速测量光栅光谱衍射效率的新方法[15],如图2所示是新方法的光路结构图,与当前常见的测量方法(如图1所示)相比,新方法的主要特点是使用了声光可调谐滤波器(AOTF)[16]、凸透镜和积分球,同时还使用高速光电探测器来采集参考光和测试光的信号。

图2 新方法的测量装置图Fig.2 Framework of the system for measuring the spectral diffraction efficiencies of a plane transmission grating using the newly proposed technique
声光可调谐滤波器用来消除现有测量方法中存在的第一种机械运动,与光栅单色器相比(光栅单色器输出波长的改变是通过移动内部的机械组件来实现的,这种操作一般能在亚秒或更长的时间内完成),声光可调谐滤波器的主要特点是其输出波长可以在微秒量级内完成改变(这是因为声光可调谐滤波器是通过调节输入超声波的频率来改变波长的,这是一个电子学过程),声光可调谐滤波器这一特性已被广泛应用于可见光-近红外吸收光谱的高速测量环境中。
(3)
图2中的凸透镜和积分球用来消除现有测量方法中存在的第二种机械运动,图中光栅测量点和凸透镜之间的距离为u,凸透镜和积分球内接收面之间的距离为v,凸透镜的焦距为f。根据凸透镜物距u、像距v和焦距f之间的数学关系式[如式(3)所示]可以看出,当入射在待测光栅上单色激光光束的波长发生改变时,所有经过待测光栅衍射的激光光束通过凸透镜的聚焦后都会照射在积分球内接收面的同一点上(严格意义上说,凸透镜的焦距与波长有关,但在这种情况下,凸透镜焦距变化产生的影响可以忽略不计)。
结合上面两种解决方案,可以看出,新方法可以完全消除现有测量方法中存在的两种耗时的机械运动。由于测量过程中没有任何机械运动的参与,同时参考声光可调谐滤波器在可见光-近红外吸收光谱高速测量环境中的应用,新方法可以成功实现光栅光谱衍射效率的高速测量。
2 实验部分
图3(a)所示是基于新方法构建的测量光栅光谱衍射效率的装置,测量系统主要包括超连续谱激光器、光栅单色器、光阑、偏振片、无偏振分束器、探测器-Ⅰ、旋转台、凸透镜、积分球、探测器-Ⅱ、双通道数据采集器和计算机。超连续谱激光器发射光谱的波段范围为390~2 600 nm,总功率约为2 W。光栅单色器的工作波段为500~1 200 nm,波长分辨率约为0.125 nm,出射单色光束光谱的半高宽为1.0~2.5 nm。线偏振片的有效工作波段为550~1 500 nm,消光比高于1 000∶1。无偏振分束器在700~1 100 nm波段范围内的分束比约为50∶50。探测器-Ⅰ是二极管硅光电探测器,其光谱响应波段为350~1 100 nm,功率探测范围为500 pW~1 W。凸透镜的直径为25.4 mm,其在632 nm波长位置处的焦距为35 mm。积分球的内径尺寸为13.5 cm,在其输出端口安装有一个硅探测器,其光谱响应波段为200~1 100 nm,功率探测范围为300 nW~1 W。待测样品是一个工作在可见光波段范围内的平面透射光栅,其线密度为1 200 line·mm-1。

图3 (a)光栅光谱衍射效率测量系统的实物图,(b)测量系统的关键几何尺寸Fig.3 (a) Physical map of the system for measuring the spectral diffraction efficiencies using the newly proposed method,(b) key geometric dimensions of the system
在这里需要指出的是,由于现有实验条件的约束和限制,在本文构建的实验装置中,我们没有采用声光可调谐滤波器来产生单色光束,而仍然利用光栅单色器来开展实验,因此严格意义上来讲,这只是一个新测量方法的验证系统,但是考虑到声光可调谐滤波器在吸收光谱高速测量环境中的广泛应用,我们认为该实验装置能全面验证新方法的可行性。
图3(b)所示是测量系统的关键几何尺寸。待测平面光栅是在正入射的情况下进行测量的,所测量的衍射级次为-1级,光栅测量点和凸透镜之间的距离为43 mm,凸透镜和积分球内接收面之间的距离为188 mm,实验中光栅光谱衍射效率测量的波段范围为550~750 nm,采样步长为1 nm。图3(b)中的绿色曲线和红色曲线分别表示波长为550和750 nm的激光光束经待测光栅衍射后的传播路径,待测平面透射光栅在两个波长位置处的衍射角分别为41.3°和64.2° (衍射级次为-1级的时候)。
3 结果与讨论
图4所示的是试验测量得到的待测平面透射光栅在550~750 nm波段范围内的光谱衍射效率。红色曲线代表利用传统方法(如图1所示)测得的P偏振光情况下的光栅光谱衍射效率,黑色曲线代表利用新方法(如图2和图3所示)测得的P偏振光情况下的光栅光谱衍射效率。从图中可以看出,大体上来说,新方法得到的光栅光谱衍射效率和传统方法测得的数据具有较好的数据一致性,但是从图4左上的局部放大图中可以看出,两种方法测得的光谱曲线之间仍然存在一定的误差。
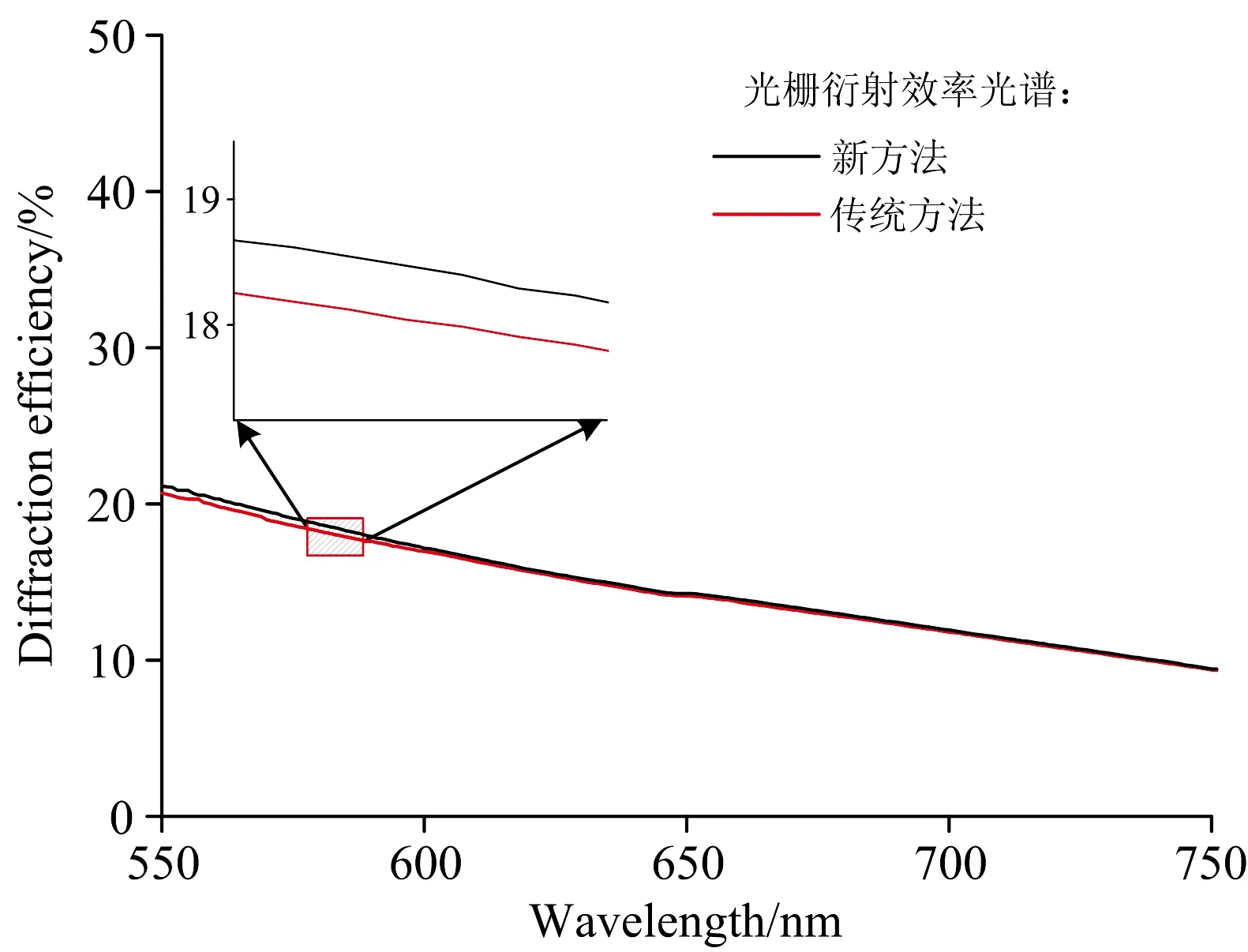
图4 光栅光谱衍射效率的测量结果
黑色曲线和红色曲线分别代表新方法和传统方法测得的P偏振光情况下的光栅光谱衍射效率
Fig.4Blackandredcurvesarethemeasuredspectraldiffractionefficienciesof,respectively,theP-polarizedlightusingthenewmethodandtheP-polarizedlightusingthecurrentlypopularmethod

表1 新方法和传统方法测得光栅光谱衍射效率的误差统计情况Table 1 The absolute error between the two measured spectral diffraction efficiencies by using the new and the currently popular methods
表1所示的是新方法和传统方法测得光栅光谱衍射效率之间绝对误差的统计情况,在550~750 nm的波段范围内,新方法和传统方法测得光栅衍射效率绝对误差的平均值为0.207%,绝对误差的最大值为0.572%。由于在很多情况下,光栅光谱衍射效率的高精度测量具有重要的意义,同时考虑到传统测量方法具有较高的精度(0.1%~0.2%),因此需要以传统测量方法为参考对象,对光栅光谱衍射效率新测量方法的主要误差来源进行分析。
4 主要误差来源分析及校正方法
结合如图2和图3(a)所示的测量构架,以及利用新方法测量光栅光谱衍射效率的主要过程[①在不放置光栅样品的时候,测量各个波长位置处探测器-Ⅱ和探测器-Ⅰ采集光强的比值k(λi);②在放置光栅后,再次测量各个波长位置处探测器-Ⅱ和探测器-Ⅰ采集光强的比值k*(λi);③光栅的光谱衍射效率可按公式η(λi)=k*(λi)/k(λi)计算得到。]。我们可以看出,光栅光谱衍射效率新测量方法一个比较明显的误差来源是凸透镜的透过率与入射角相关。在测量k(λi)的步骤中,不同波长的单色激光光束都是沿凸透镜的光轴传输时,如图5(a)中的黑色直线所示,然而在测量k*(λi)的过程中,不同波长的单色激光光束经过光栅的衍射后,以不同的入射角照射在凸透镜上,并被聚焦到积分球内表面上,如图5(a)中的彩色线条所示。由于凸透镜的透过率与入射角有关,因此这会造成测量误差。

图5 (a)黑色直线:放置光栅前不同波长单色激光光束沿凸透镜的光轴传播;彩色线条:不同波长的单色激光光束经过光栅的衍射后,以不同的入射角照射在凸透镜上;(b)黑色曲线:放置待测光栅前,激光沿凸透镜的光轴传播时的透射光谱;红色曲线:经过光栅衍射后,不同波长激光光束以不同入射角通过凸透镜时的透过率Fig.5 (a) Black line:Before inserting the grating,the monochromatic laser beams of different wavelengths propagate along the optical axis of the convex lens;color lines:After diffracted by the grating,the laser beams of different wavelengths irradiate the convex lens at different incident angles;(b) Black line:transmission spectrum of the convex lens laser when the laser beam propagates along its optical axis;red curve:transmission spectrum of the convex lens laser when the laser beam of different wavelengths irradiate the convex lens at different incident angles
通过利用Tracepro软件模拟本实验中激光光束传播通过凸透镜的行为,我们得到如图5(b)所示的光学模拟结果。图5(b)中黑色曲线表示550~750 nm波段范围内激光光束沿凸透镜光轴传播时的透射光谱,图5(b)中红色曲线所示是不同波长激光光束以不同入射角度[波长和入射角度的粗略对应关系可以查看图3(b)]经过凸透镜的透射光谱。
根据上述数值模拟结果,新方法测得的光栅光谱衍射效率可以按照式(4)进行误差矫正。
(4)
式(4)中η测量值(λi)代表新方法试验测到的光栅衍射效率,η校正值(λi)是经过误差矫正后的衍射效率值,T(λi)是图5(b)中黑色曲线代表的透射光谱,T*(λi)图5(b)中红色曲线代表的透射光谱。
图6中的黑色曲线是新方法测得的光栅光谱衍射效率,红色曲线代表传统方法测得的光栅光谱衍射效率,蓝色曲线表示新方法得到的光栅光谱衍射效率经过误差矫正后的结果。从图6左下部的局部放大图中可以看出,与新方法直接测得的结果相比,经过误差矫正后,新方法得到的光栅光谱衍射效率和传统方法测得的光谱曲线具有较好的一致性。
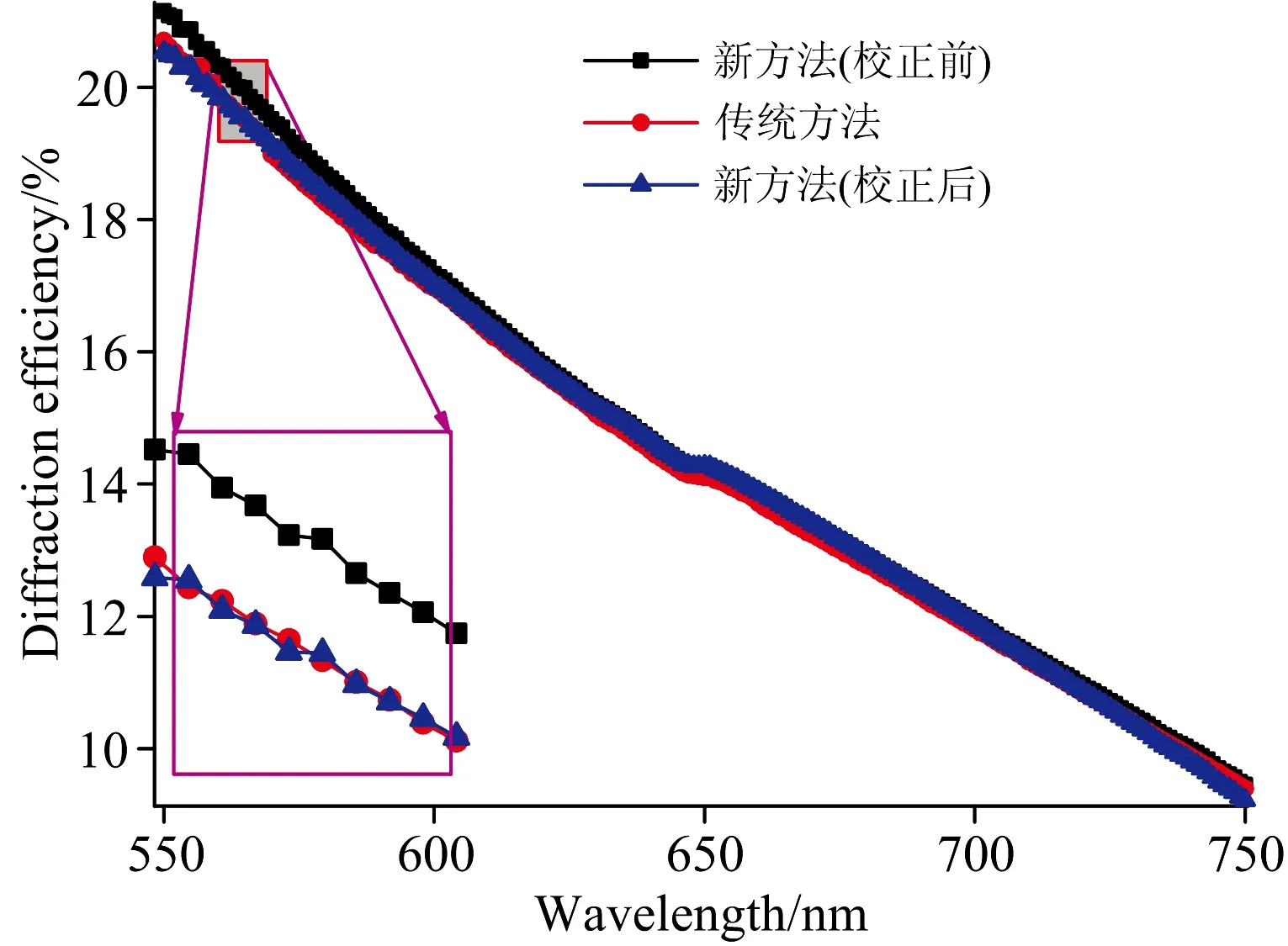
图6 黑色曲线:新方法测得的光栅光谱衍射效率;红色曲线:传统方法测得的光栅光谱衍射效率;蓝色曲线:经过误差矫正后新方法得到的光栅光谱衍射效率Fig.6 Blackcurve:the spectral diffraction efficiencies measured by the new method;red curve:the spectral diffraction efficiencies measured by the currently popular method;blue curve:the corrected spectral diffraction efficiencies measured by the new method
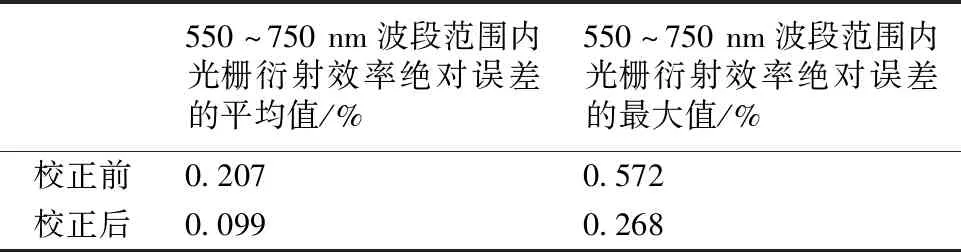
表2 校正前后新方法和传统方法测得光栅光谱衍射效率的误差统计情况Table 2 The absolute error between the two measured spectral diffraction efficiencies by using the new (before and after correction) and the currently popular methods
表2所示的是矫正前后新方法和传统方法测得光栅光谱衍射效率之间绝对误差的统计情况,在550~750 nm的波段范围内,可以看出,经过误差校正后,新方法与传统测量方法之间的相对误差的平均值已降到0.099 2%,考虑到传统测量方法的测量精度约为0.1%,我们认为新方法的主要误差来源已经得到有效的校正。
5 结 论
对光栅光谱衍射效率测量新方法的主要误差来源进行了分析,并提出了相应的校正方法。测量实验和数据分析结果表明,本文提出的误差校准方法能成功消除新方法的主要误差来源。
- 光谱学与光谱分析的其它文章
- Synthesis and Spectroscopic Characterizations on the Complexation of Three Different Metal Ions Ba(Ⅱ), Ni(Ⅱ),and Ce(Ⅲ) with Atenolol Drug Chelate
- An Estimation Study to Determine the Percentage of Hydroquinone Levels in situ Skin Lightening Creams Using GC-MS and HPLC Spectroscopic Instruments
- 无人机高光谱的玉米冠层大斑病监测
- 叶表面偏振反射测量对冬小麦氮含量高光谱估算的提升
- 联苯菊酯分子的拉曼光谱研究
- 激光诱导击穿光谱的环形扫描探测与元素分布分析

