基于贝叶斯平均法的洪水分类组合预报研究
刘 恒
(辽宁省水利水电科学研究院有限责任公司,辽宁 沈阳 110003)
0 引 言
单纯依靠改变模型参数来提高不同类型洪水的预报精度,虽然在一定程度上能提高洪水预报精度;但具有一定的局限性,仍然无法避免单个水文模型结构的不确定性对预报结果的影响。目前,国内外已经提出很多种水文模型,分别在不同的地区和流域发挥重要作用;但是,每种水文模型都是学者对自然界降雨径流及洪水运动规律的一种理解和概化,无法全面描述实际的产汇流过程[1]。这也表明每种模型都存在一定的优缺点,不能说明哪种水文模型在任何情况都完全优于其他模型[2-3]。既然单个模型存在一定的缺陷,那么能不能将几种模型的预报结果进行组合,尽可能地减少单一模型结构不确定性对预报结果的影响,降低模型结构带来的误差。基于这一想法,国内外学者提出了多模型组合预报的概念。即,综合多个模型的预报结果,提高整体预报精度。目前,对组合洪水预报方法有很多,早期的水文模型综合研究采用简单平均法、加权平均法、模糊数学法、神经网络模型、贝叶斯平均法等方法。这些方法弥补了单个模型的缺陷,充分发挥每个模型的优势[4]。为进一步提高预报精度,将同时考虑模型参数不确定性与模型结构不确定性对预报结果的影响,本文将在多组概念性水文模型的基础上,采用神经网络、遗传算法、贝叶斯、蒙特卡罗等算法,将单模型的分类洪水预报与多模型的组合预报结合起来,建立分类洪水组合预报模型,综合考虑各模型的优势,从而提高预报精度。关于概念性水文模型、基于BP神经网络的洪水分类,以及基于遗传算法的参数率定相关论文比较多,本文在此不对相关理论进行赘述。
1 基于贝叶斯模型平均法的组合预报
1.1 贝叶斯平均法基本原理
贝叶斯模型平均法(BMA)是由A. E. Rafery等人提出的,利用多模型进行概率预报的统计处理方法[5],是一种基于贝叶斯理论,将模型本身的不确定性考虑在内的统计分析方法。作为一种能够提高模拟结果的有效综合计算方法,贝叶斯模型平均方法是通过综合几个模型预报值的后验分布来推断预报量的更可靠概率分布分析工具。它不仅能提供一个综合的预报值,同时可以获取描述模拟结果的不确定区间,为用户通过更多的参考依据,被国内外学者广泛应用于众多研究领域[6-9]。贝叶斯平均法克服了其他预测模型的一系列确定,包括未考虑主观先验信息、没有提取各模型正确的预测信息、没有考虑模型不确定性等。其基本表达式如下
(1)
式中,yBMA为BMA法的组合预测值;yMk为单个模型Mk的预测值;t为变量;P(Mk|D)是给定数据D情况下,模型的后验概率。BMA法的实质:以单个模型的后验概率为权重,对单一模型的预测值进行加权平均得到贝叶斯模型均值。
1.2 基于贝叶斯平均法的组合预报
近年来,BMA方法被应用到洪水预报领域,将多个水文模型的预报结果进行组合,这对于提高我国水文预报的水平具有重要的现实意义和科学价值[10-11]。实现对各水文模型的预报流量序列进行加权平均,获得组合预报值和预报区间[12],具体模型构建过程如下:
1.2.1概率密度函数
设Q为预报变量,D=[X,Y]为实测数据(X为输入资料,Y为实测的流量资料),f=[f1,f2,…,fk]是K个模型预报的集合。根据贝叶斯模型平均法的理论,BMA的概率要表示为
(2)
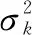
首先将模型预报值和实测流量都用Box-Cox转化方法进行正态转化,可以方便BMA计算。因此,综合预报量Q的后验分布实际上是以后验模型概率p(fk|D)为权重,对所有模型的后验分布pk(Q|fk,D)进行加权的一个平均值。
1.2.2期望与方差计算
BMA平均预报值是单个模型预报值的加权平均结果。如果单个模型预报值和实测流量均服从正态分布,则BMA平均预报值

(3)
(4)
1.2.3正态转换
由于实测和预报流量序列都存在一定的不确定性,不符合正态分布的规律,如果在原始数据基础上直接推求概率密度函数,将该计算带来很大的麻烦。因此,首先要将这些数据采用一定的转换规则将其转为服从正态分布的数据。本文采用Box-Cox(博克斯-卡克斯)转换法,即
(5)
式中,odt是为t时刻未转化的原始数据;tdt是为转化后的数据;λ是为Box-Cox转化系数。因为EM算法中需要把模型预报值结合计算,所以对所有的模型预报值和实测流量,都采用同一个转化系统λ。
1.2.4期望最大化算法
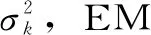

(6)
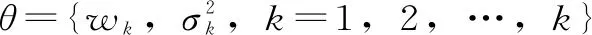
(1)初始化。设Iter=0
(7)
(8)

(2)计算初始似然值。即
(9)
(3)计算隐藏变量。设Iter=Iter+1
(10)
(4)计算权重
(11)
(5)计算模型预报误差
(12)
(6)计算似然值
(13)
(7)检验收敛性。如果l(θ)(Iter)-l(θ)(Iter-1)小于或等于预先设定的允许误差,就停止;l(θ)(Iter)-l(θ)(Iter-1)小于或等于预先设定的允许误差,就停止;否则回到步骤(3)。
2 基于神经网络和贝叶斯平均法的分类组合预报
基于神经网络和贝叶斯平均法的分类多模型组合预报的基本原理是将洪水分类预报与多模型组合预报相结合。首先,基于BP神经网络模型实现洪水的分类,将洪水划分为高水、中水、低水三类;然后,针对不同类型洪水采用遗传算法进行参数率定,获取每种类型洪水对应的最优或近似参数组,实现分类洪水预报。在分类洪水预报的基础上,本文选取新安江、大伙房、辽宁指数3个概念性水文模型(工程水文学),使用BMA方法将3模型针对不同类型洪水的预报结果进行综合,在综合之前需要对实测和预报序列进行正态转换。然后以实测序列隶属于某个水文模型后验概率为权重,对所选单项模型方法的预报变量进行加权平均,实现了不同水文模型预报的合成及概率预报。将模型本身参数与结构的不确定性考虑在内,最终获得分类洪水最优参数的多模型组合预报值及概率区间。分类多模型组合预报包括模型构建和模型计算两个环节。
2.1 模型构建
(1)洪水分类模型构建。基于BP神经网络构建洪水分类模型,采用历史典型洪水对模型结构进行率定与检验,最终构建出基于BP神经网络的在线洪水分类模型[13]。
(2)不同类型洪水模型参数率定。基于遗传算法对不同类型洪水(高水、中水、低水)的不同模型(新安江模型、大伙房模型、辽宁指数模型)进行参数率定,从而获得每种类型洪水对应不同模型参数。
(3)权重计算。对实测流量与预报流量正态转换,采用BMA方法(见图1)分别对每种类型洪水3个水文模型的预报流量序列进行分析计算,采用期望最大化算法(EM)估计BMA中的未知参数,从而获得获取3种类型洪水对应的3组权重[14]。

图1 分类组合预报流程
2.2 模型计算
(1)在线分类。输入实测降雨及洪水数据,基于BP神经网络在线洪水分类模型对实时洪水进行分类,确定该场次洪水所属类别。
(2)分类预报。根据洪水类别,分别采用大伙房模型、新安江模型、辽宁指数模型3个水文模型进行预报,可获得3组预报流量序列。
(3)组合预报。根据每种类型洪水对应的权重组合,对新安江、大伙房、辽宁指数3种模型的预报流量序列进行组合,从而获得每种类型洪水的预报均值和预报区间。
3 基于蒙特卡罗法的不确定性区间估计


(14)

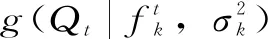
(3)重复步骤(1)和(2)M次。M是为生成不确定性区间取样的总个数,令M=1 000。BMA在任意时刻t的1 000个样本值由上述方法取样得到以后,将他们从小到大排序,BMA的90%预报不确定性区间就是5%和95%分位数之间的部分。
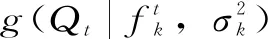
4 分类洪水组合预报模型实例验证
4.1 基础资料
选取大伙房水库1960年~2016年的25场历史典型洪水作为本研究的基础资料,并将洪水分成3类,包括5场高水、9场中水、11场低水。选择20场典型洪水资料作为模型的率定期,包括4场高水、7场中水、9场低水。另外5场典型洪水资料进行模型的检验和比较,其中包括1场高水、2场中水、2场低水。历史洪水信息见表1。
4.2 验证与分析
4.2.1正态转换
采用P-P图来判断实测流量和不同模型(新安江模型、大伙房模型、辽宁指数模型)的预报流量是否符合正态分布。P-P图是一种判断数据序列是否符合正态分布的重要手段,它是以期望的累积概率作为纵坐标,以观测的累积概率作为横坐标,把样本值以散点的形式落在直角坐标系中。如果样本序列服从正态分布,则样本值应集中落在对角线的附近。如果实测流量和预报流量不服从正态分布,采用Box-Cox转换法对实测流量和预报流量进行正态转换。本文采用Minitab工具实现数据的Box-Cox转换,采用SPSS工具实现P-P图的绘制。以“20130816”实测洪水为例,转换前和转换后的实测数据正态频率曲线见图2和图3。

图2 转化前“20130816”实测流量
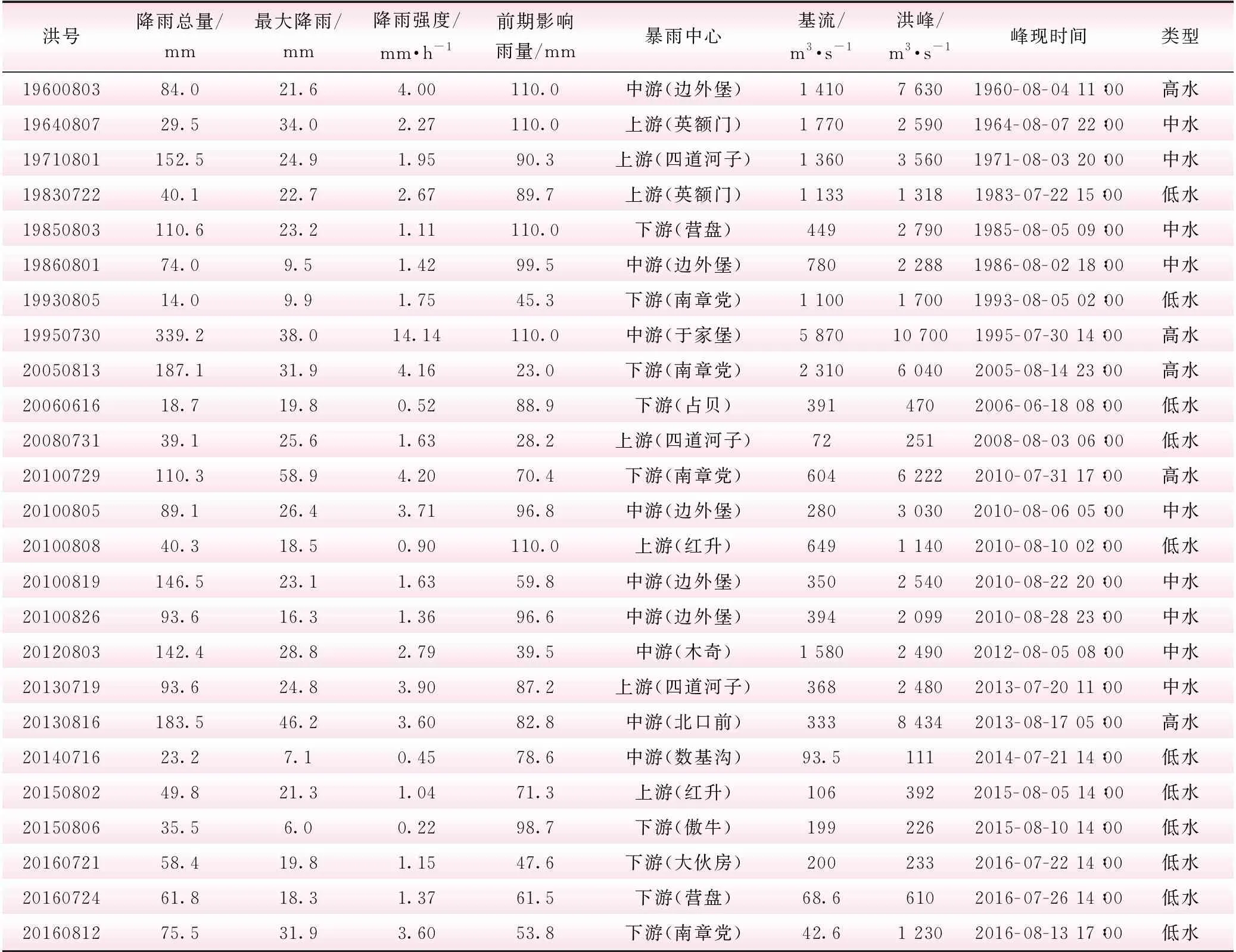
表1 历史洪水信息

图3 转化后“20130816”实测流量
由图2、3可以看出,“20130816”实测流量在转换前是高度不服从正态分布的,经过Box-Cox转换后,数据明显接近正态分布。
4.2.2参数估计

表2 不同流量级别的模型参数估计值
由表2可见,在高水情况下,大伙房模型的权重系数明显高于新安江模型和辽宁指数模型的权重系数,分别为0.72 、0.17、0.11,说明基于超渗产流机理的大伙房模型针对高水具有较好的预报效果;在中水情况下,新安江模型、大伙房模型和辽宁指数模型的权重系数基本相同,分别为0.36、0.33 、0.31,说明3个模型针对中水的预报效果基本相同;在低水情况下,新安江模型、辽宁指数模型的权重系数要高于大伙房模型的权重系数,分别为0.37、0.21、0.42 ,说明基于蓄满产流机理的新安江模型、辽宁指数模型针对低水具有较好的预报效果。其原因为:在中国北方地区很多地方是超渗产流与蓄满产流交替产生,当降雨量或雨强较大时,以超渗产流为主;当降雨量或雨强较小时,以蓄满产流为主。

表3 分类组合预报率定期预报精度分析
注:NXAJ为分类洪水新安江模型、NDHF为分类洪水大伙房模型、NLNZS为分类洪水辽宁省指数模型、NBMA为分类洪水贝叶斯平均法。
4.2.3评定指标
本文采用相对误差及确定性系数两个指标来分别评定单个模型分类预报结果和BMA组合预报的预报精度,如上所述;同时,采用覆盖率作为评定指标,对BMA组合预报的预报区间的优良性进行评定。覆盖率(CR)是指预报区间覆盖实测流量数据的比率,为最常用的预报区间评价指标。计算公式如下
(15)
式中,At为t时刻预报区间是否覆盖实测流量,如果覆盖实测流量则为1,否则为0,NT为预报时间序列长度。CR值越大,表示预报区间覆盖率越高。
4.2.4预报值对比分析
采用上述估计的参数对率定和检验的历史洪水,分别采用单个模型(新安江模型、大伙房模型和辽宁指数模型)和分类贝叶斯平均法进行洪水模拟,获取每场洪水的预报结果(洪峰、峰现时间和预报区间),并采用洪峰相对误差、峰现时间误差和确定性系数对模拟结果进行评定,率定洪水及检验洪水特征值统计结果绝对值见表3和表4。
按照洪水类型(高水、中水和低水)对率定期和检验期预报结果绝对值进行统计,统计结果如表5所示。
由表3、4可以看出,在率定期和检验期的25场洪水中,分类组合预报的洪峰相对误差比单个模型小,洪峰相对误差小于等于20%的洪水次数为22,合格率达到88%;峰现时间误差小于等于1个时段的洪水次数为21,合格率为84%。因此,分类组合预报的洪峰预报标准可达到甲级标准,显著提高了不同类型洪水的预报精度。
从表5统计结果可看出,除极少数的洪水以外,分类洪水贝叶斯平均法预报效果优于单个模型预报效果。在率定期和检验期的25场历史典型洪水中,总体平均洪峰相对误差绝对值从12.79、10.9、12.77降到7.05,总体平均峰现时间误差从1.21、1.03、1.17 h降到0.64 h,总体平均确定性系数从0.85、0.86、0.83提高到0.90。这表明分类洪水贝叶斯平均法可以应用于大伙房水库上游流域,效果整体上优于单个模型情况,方法可行、有效。

表4 分类组合预报检验期预报精度分析

表5 分类组合预报不同洪水类型统计结果
为了更形象地说明BMA在水文模型综合预报中的效果,选择“20130816”洪水作为典型洪水,分别绘制降雨、实测流量,以及NXAJ模型、NDHF模型、NLNZS模型和NBMA模型的预报流量过程线图,洪水模拟过程如图4所示。

图4 20130816洪水单模型预报及NBMA组合预报过程
从图4可见:分类组合预报模型比单个模型能够更好地模拟每场洪水的洪峰流量、峰现时间及洪水过程。分类组合预报的洪水过程与实测水位拟合度明显优于单个水文模型,分类组合预报模型集合了单个模型的优势,其预报结果更贴合实测值。总体上,分类组合预报可以达到令人满意的预报精度,无论是洪峰流量、峰现时间还是洪水过程的模拟,其预报效果都要优于单个模型。这表明分类组合预报可有效提高预报精度,该方法是可行的。
4.2.5预报区间对比分析
除均值预报外,分类贝叶斯平均法还可以给出预报区间。采用上述估计的参数对率定期和检验期的25场历史典型洪水,采用分类贝叶斯平均法进行洪水模拟,获取每场洪水的预报区间,并采用覆盖率作为指标来分析比较NBMA组合预报的90%预报区间与实测值之间的对比,从而分析比较其预报不确定性区间的优良性。分类贝叶斯平均法在整个流量序列90%置信度的置信区间率定期和检验期预报结果分别见表6、7。
按照洪水类型对率定期和检验期分析结果进行统计,统计结果如表8所示。
由表6~8可知,分类贝叶斯平均法计算的预报区间对实测值的覆盖率在高水部分时效果较好,实测洪峰流量均在置信区间范围内,覆盖率均在80%以上,平均覆盖率为88.65%;但是中水和低水部分的平均覆盖率较低,分别为52.38%和33.46%。
为了更形象地说明NBMA在水文模型综合预报中的效果,以“20130816”洪水为例,分别采用NBMA方法和单个模型进行计算,绘制出降雨过程、实测流量、预报均值、90%置信区间的过程图,从而分析预报区间的优良性(见图5)。
从图5预报区间分布图可以看出,“20130816”洪水的绝大多数的实测数据均落于90%置信区间内,区间对实测值的覆盖度为88.32%。基于NBMA的预报方法定量的提供了洪水流量范围,使决策人员定量地考虑预报的不确定性,为防洪规划提供了依据。

表6 分类组合预报模型率定期预报区间分析 m3/s
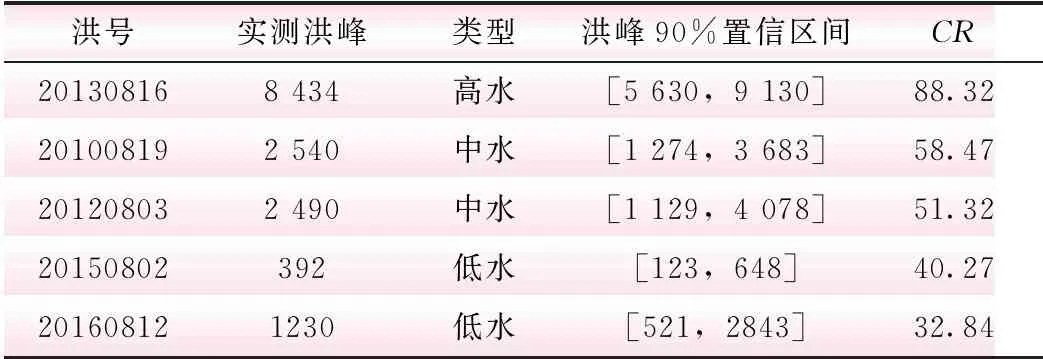
表7 分类组合预报模型检验期预报区间分析 m3/s

表8 不同洪水类型预报区间统计结果

图5 NBMA模拟序列90%不确定性置信区间
4.3 结果分析
综上所述,贝叶斯模型加权平均方法是通过综合几个模型预报值的后验分布来推断预报量的更可靠概率分布分析工具。它不仅能提供一个综合的预报值,还能提供一个综合的预报区间。本文采用3个水文模型,统一用遗传算法率定参数,得到9组不同的预报值用于BMA方法的综合;然后对BMA和组成其3个模型从预报精度和预报不确定区间这两方面进行了详细的比较和分析,得到如下结论:
(1)相对误差和确定性系数两个指标的值表明,BMA方法在一定程度上提高了预报精度,对于整个流量序列,BMA的预报值比单个模型的预报值都高;对于不同洪水类型,BMA的预报精度在高水和低水部分都高于单个模型。
(2)利用BMA90%不确定性区间对模型结构不确定性进行评价。
综合而言,对BMA和组成其单个模型比较分析表明,BMA方法降低了单一水文预报结果的不确定性,能够在一定程度上提高预报精度。更重要的是,BMA能够提供可靠的预报不确定性区间,为防洪决策提供参考依据。
5 结 论
本文针对水文模型结构的不确定性,基于贝叶斯平均法开展多模型组合预报研究。综合考虑模型参数及模型结构不确定性共同对预报结果造成的影响,在洪水分类预报研究成果基础上,创新性构建了基于BP神经网络和贝叶斯平均法的洪水分类组合预报模型。以大伙房水库为实例验证区域,选取1960年~2016年的25场历史典型洪水作为本研究的基础资料,实现对模型的率定与检验。结论如下:
(1)通过贝叶斯平均法推求新安江模型、大伙房模型、辽宁指数模型3个模型对应不同类型洪水的预报流量序列的均值、方差,利用后验概率作为每个模型所占权重,反映了每个模型的预报效果。分析表明,在高水情况下,大伙房模型的权重系数明显高于新安江模型和辽宁指数模型的权重系数,分别为0.72、0.17、0.11,说明基于超渗产流机理的大伙房模型针对高水具有较好的预报效果;在中水情况下,新安江模型、大伙房模型和辽宁指数模型的权重系数基本相同,分别为0.36、0.33、0.31,说明三个模型针对中水的预报效果基本相同;在低水情况下,新安江模型、辽宁指数模型的权重系数要高于大伙房模型的权重系数,分别为0.37、0.42、0.21,说明基于蓄满产流机理的新安江模型、辽宁指数模型针对低水具有较好的预报效果。分析原因:在中国北方地区很多地方是超渗产流与蓄满产流交替产生,当降雨量或雨强较大时,以超渗产流为主,当降雨量或雨强较小时,以蓄满产流为主。
(2)按照洪水类型对率定期和检验期预报结果进行统计的结果表明,分类组合预报效果明显优于单个模型预报效果,平均洪峰相对误差绝对值从10.43、9.43、10.15降到6.36,平均峰现误差从1.19 h、1.02 h、1.6 h降到0.54 h,平均确定性系数从0.85、0.86、0.83提高到0.90。选择“20130816”洪水作为典型洪水进行过程分析,检验表明组合预报结果拟合度明显优于单个水文模型,分类组合预报模型集合了单个模型的优势,预报结果更贴合实测值。贝叶斯平均法不仅能提高预报精度,还能推求出性质更为优良的预报区间,对预报不确定性的定量评估,提高预报的可靠性。分析表明,实测值的覆盖率在高水部分时效果较好,实测洪峰流量均在置信区间范围内,覆盖率均在80%以上,平均覆盖率为88.65%,中水和低水部分的平均覆盖率较低,分别为52.38%和33.46%。

