不确定需求下零售商最优定价订购联合决策

张圣忠，田爱玄，李继东

(长安大学 经济与管理学院，陕西 西安 710064)

生产技术革新的日益加快、市场竞争的不断加剧和消费偏好多样化的日趋明显，均使得市场需求不确定性成为常态。特别是对于新上市或更新换代速度较快的产品来说，短生命周期特性逐渐增强，零售商难以掌握其完全市场信息，存在库存积压及货物短缺的风险。此外，随着同质产品的不断冲击，如何在需求不确定情形下制定价格及订购决策具有重要的现实意义。

报童模型作为生产决策的经典模型，被广泛用来解决短生命周期产品的定价与订购决策问题。然而，传统的报童模型将销售价格视为外生变量，忽视价格因素对产品需求的影响。事实上，零售商往往会通过调整产品价格来刺激或抑制需求，导致市场需求依赖销售价格。WHITIN[1]首次将价格作为内生变量引入报童模型，假设需求分布依赖销售价格，得到最优订货量关于销售价格的函数表达式。POLATOGLU[2]考虑了市场需求扰动项分别服从均匀分布的加性需求模式和服从指数分布的乘性需求模式下报童模型定价与订购策略。PETRUZZI等[3]对单周期随机库存问题进行了全面回顾及推广，在两种需求模式下求得最优联合定价与订购决策。近年来，报童模型的联合定价与订购问题得到了更广泛的拓展。文献[4]和文献[5]在加性需求模式和乘性需求模式下，分别讨论了考虑缺货惩罚、损失规避的零售商最优定价订货联合决策问题。在此基础上，陈克贵等[6]将缺货加急订货成本考虑在内，对过度自信零售商的最优定价及订货联合决策进行了探讨。GULER等[7]将产品参考价格引入加性随机需求函数中，研究具有参考效应的联合库存与定价策略。RAZA[8]研究了考虑缺货成本和持有成本情形的报童模型联合定价与订购问题。总体而言，上述两种需求模式下的联合定价与订购策略研究大多以已知市场需求的随机分布为前提，而销售环境的复杂和需求的多样使得这一假设不再适应现实场景。

因此，不少学者开始研究不完全需求信息下自由分布的报童模型。如SCARF[9]利用最小最大方法对仅有市场需求均值和方差信息的报童模型库存问题进行研究。在此基础上，GALLEGO等[10]将自由分布的报童模型推广到订购成本固定、二次订购、多产品及随机合格率4种情形中。MOON等[11-12]研究了当产品库存降低到某一阈值时顾客购买迟疑的情形，分别给出期望利润最大、考虑销售损失惩罚的库存决策。刘开军等[13-14]以利润最大化为目标,在需求信息未知情形下，分别讨论了考虑连续型需求及离散型需求的最优库存策略。针对不完全需求信息下的联合定价与订购问题，张文思等[15]分别在需求分布未知的加性模式和乘性模式下，讨论带有资源约束和数量折扣的多产品报童模型的联合定价与订购策略，得出了最坏分布下的最优期望利润。ZHOU等[16]探讨了具有部分需求信息的双渠道报童模型最优定价及最优订购量问题。

上述关于需求未知情形下的联合定价与订购问题的研究，仍可通过销售数据或调研数据获得部分市场需求信息，即以随机市场需求为基础并应用概率论对市场需求频率进行处理。然而现实中，由于环境的复杂多变，不乏有需求信息匮乏的情形，尤其对于初上市的新兴产品来说，销售数据和调研数据的缺乏导致市场需求的均值及方差均无法获取，不能得出需求发生频率及准确的分布函数，因此这类需求不再是随机需求，而是不确定需求[17]。针对不确定需求，必须邀请领域专家来评估市场需求发生的信度。调查显示，人们对于不确定事件的估计范围比实际情况要宽得多，即事件的估计概率分布和实际发生频率间存在很大的差异[18]，在这种情况下，概率论具有一定的局限性，甚至可能导致反直觉的结果[19]。为处理不确定现象，度量和模拟人类信度的不确定性，不确定理论应运而生，如LIU[20]提出了不确定变量的建模体系和数学处理规则。此外，作为经典概率论的补充，虽然不确定理论中信度满足规范性、对偶性、次可加性，但不确定理论下的乘积测度是各事件的不确定测度最小值，而概率论中的乘积测度为各个事件发生的概率测度乘积[21]。因此，不确定变量和随机变量遵循不同的处理规则。目前，不确定理论被广泛应用于设施选址[22]、金融投资[23]、运输调度规划[24]等领域。文献[17]首次应用不确定理论解决报童模型最优订购量问题，证实了不确定理论在报童模型决策问题中的适用性。DING等[25]将不确定理论拓展到多产品报童问题和不确定随机报童问题中。黄世华等[26]对经典库存问题进行推广，定义风险函数并基于不确定理论研究了库存控制最优策略。HUANG等[27]探讨了制造成本、销售成本为不确定变量的替代品最优定价问题。

从现有文献来看，有关联合定价订购问题的研究多集中于对随机市场需求的探讨，而缺少对不确定需求的关注。此外，目前不确定理论在报童模型中的应用主要集中于单一订购或单一定价策略研究，较少文献研究不确定理论在最优定价与订购联合决策问题中的应用。因此，针对此类不确定需求，笔者应用不确定理论，以现有的加性需求模式和乘性需求模式为基础，假设市场需求扰动为不确定变量而非随机变量，对其进行不确定建模处理，探讨零售商的最优定价与订购联合决策问题，以得到最优定价和库存因子的解析表达式，证明其存在性和唯一性，揭示价格敏感因子和市场需求扰动项方差对最优决策和期望利润的影响。

1 理论基础

不确定理论通过信度描述不确定变量，并给出信度的处理框架和规则,为主观不确定现象建模提供了理论基础和分析工具。

令Γ为非空集合，L为Γ上的σ-代数,M为从L到[0, 1]上的集函数,Λ∈L为一个事件，若M满足：

(1)规范性公理：对于全集Γ，M{Γ}=1 。

(2)对偶性公理：对于任意Λ，M{Λ}+M{Λc}=1成立。

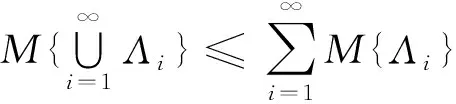
定义1记ξ为不确定变量，ξ为(Γ,L,M)到实数集上的可测函数, 即对任意实数Borel集, 集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}为一个事件；定义ξ的分布函数为Φ(x)=M{γ|ξ(γ)≤x},x∈R。

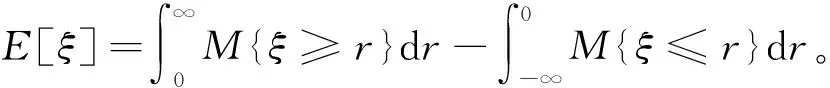
定义3对于所有的α∈(0,1)，当且仅当M{ξ≤Φ-1(α)}=α时，函数Φ-1为不确定变量ξ的逆不确定分布。

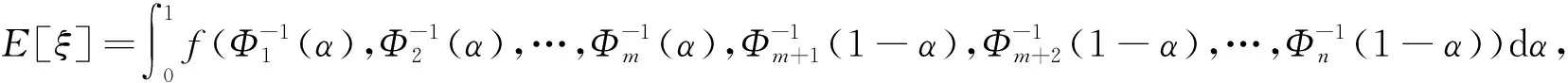
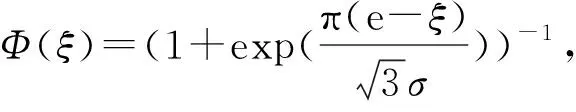
2 问题描述

基于不确定理论，考虑不确定需求依赖价格情形的报童模型最优定价与订购联合决策问题。假定市场需求为不确定需求ξD，零售商以最大化期望利润为目标，向制造商订购数量为y、批发价格为q的产品，并以价格p向消费者售卖产品，销售期结束后，零售商剩余产品的残值为h，p>q>h，零售商利润函数为：

3 模型分析

采用需求依赖价格情形下报童问题的两种常用需求函数：加性需求模式和乘性需求模式，探究零售商最优定价与订购决策问题。其中，加法需求模式为ξD=D(p,ε)=d(p)+ε，d(p)=a-bp,a>0,b>0；乘法需求模式为ξD=D(p,ε)=d(p)ε，d(p)=ap-b,a>0,b>1。其中d(p)表示与价格相关的均值需求；a表示市场规模；b表示市场需求的价格敏感因子；p表示产品销售价格；ε表示与价格无关的需求扰动项。

3.1 加性需求模式下最优定价与订购决策

加性需求模式下，不确定市场需求ξD=D(p,ε)=d(p)+ε，d(p)=a-bp,a>0,b>0，定义库存因子z=y-d(p),则y=d(p)+z。由于ξD≥0、y≥0，可知z≥A。零售商利润函数可转化为：

f(z,p)=

(2)

因此，零售商最大期望利润可表示为：

maxE[f(z,p)]

s.t.z≥A,p≥0

(3)

由于ε为不确定变量，ξD和f(z,p)为ε的函数，则ξD和f(z,p)均为不确定变量。因此，零售商最优销售价格和订货量(p*,y*)决策问题转化为确定最优销售价格和库存因子(p*，z*)问题。

(4)

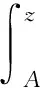
3.2 乘性需求模式下最优定价与订购决策

乘性需求模式下，不确定市场需求ξD=D(p,ε)=d(p)ε，ε∈[A,B]，d(p)=ap-b,a>0,b>1。定义库存因子z=y/d(p)，则y=d(p)z，由于ξD≥0、y≥0，可知z≥A。零售商利润函数转化为：

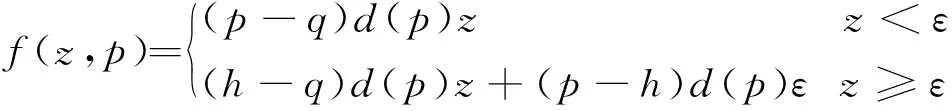
(5)

同理，零售商最优销售价格和最优订货量(p*，y*)决策转化为确定最优销售价格和最优库存因子(p*，z*)问题。

命题2乘性需求模式下，不确定市场需求ξD=D(p,ε)=ap-bε，且扰动项ε的不确定分布函数Φε(x)连续，对于任意的z(A≤ε≤B)，存在唯一最优的销售价格p*(见式(6))。若ε具有IFR，则库存因子z*可由b(q-h)[Λ(z)-zΦε(z)]+(q-hΦε(z))(z-Λ(z))=0确定。

(6)

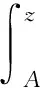
4 数值分析

4.1 价格敏感因子对零售商最优决策和期望利润的影响

(1)针对加性需求模式，假设ε服从正态不确定分布N(120,4)，保持参数a=100、q=11.5、h=7.6不变，令价格敏感因子b从1到7变化，探讨价格敏感因子对零售商最优决策和期望利润的影响。其中，加性需求下b对最优销售价格p*的影响如图1所示，可以看出加性需求模式下，最优销售价格p*随价格敏感因子b的增大而减小，最终趋于稳定。这是因为加性需求模式下，市场需求是价格敏感因子b的线性减函数，b增加导致市场需求减少，此时零售商会通过降低销售价格来减小需求变异系数，而受成本限制，最优销售价格不会无限下降。

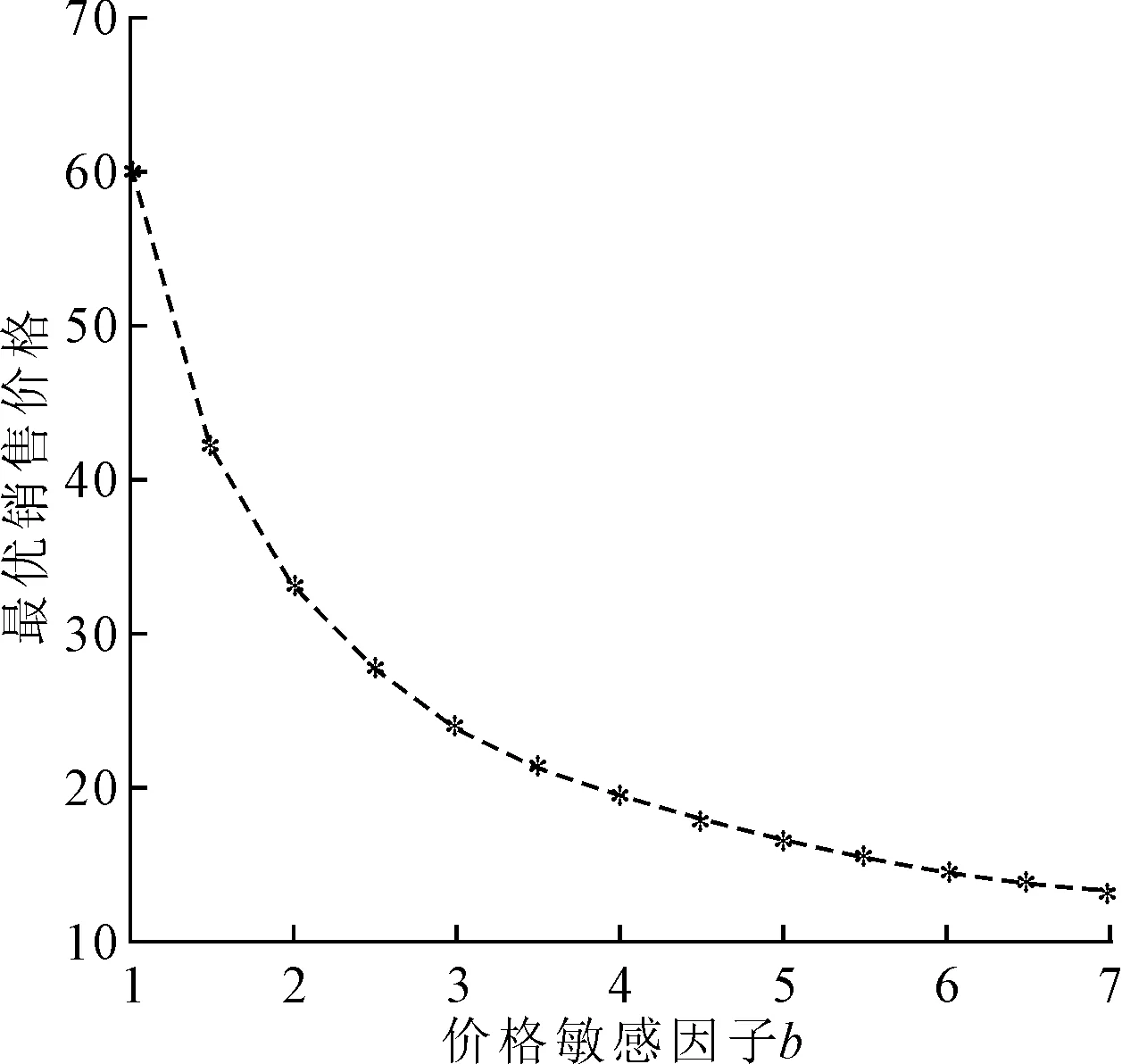
图1 加性需求模式下b对最优销售价格p*的影响

加性需求模式下b对最优订货量y*及均值需求d(p)的影响如图2所示，可以看出最优订货量y*及均值需求d(p)呈现相同的变化趋势，均为价格敏感因子b的减函数。这是因为在面对不确定需求时，零售商倾向把握均值需求来降低风险，即降低订购量来保证利润空间。

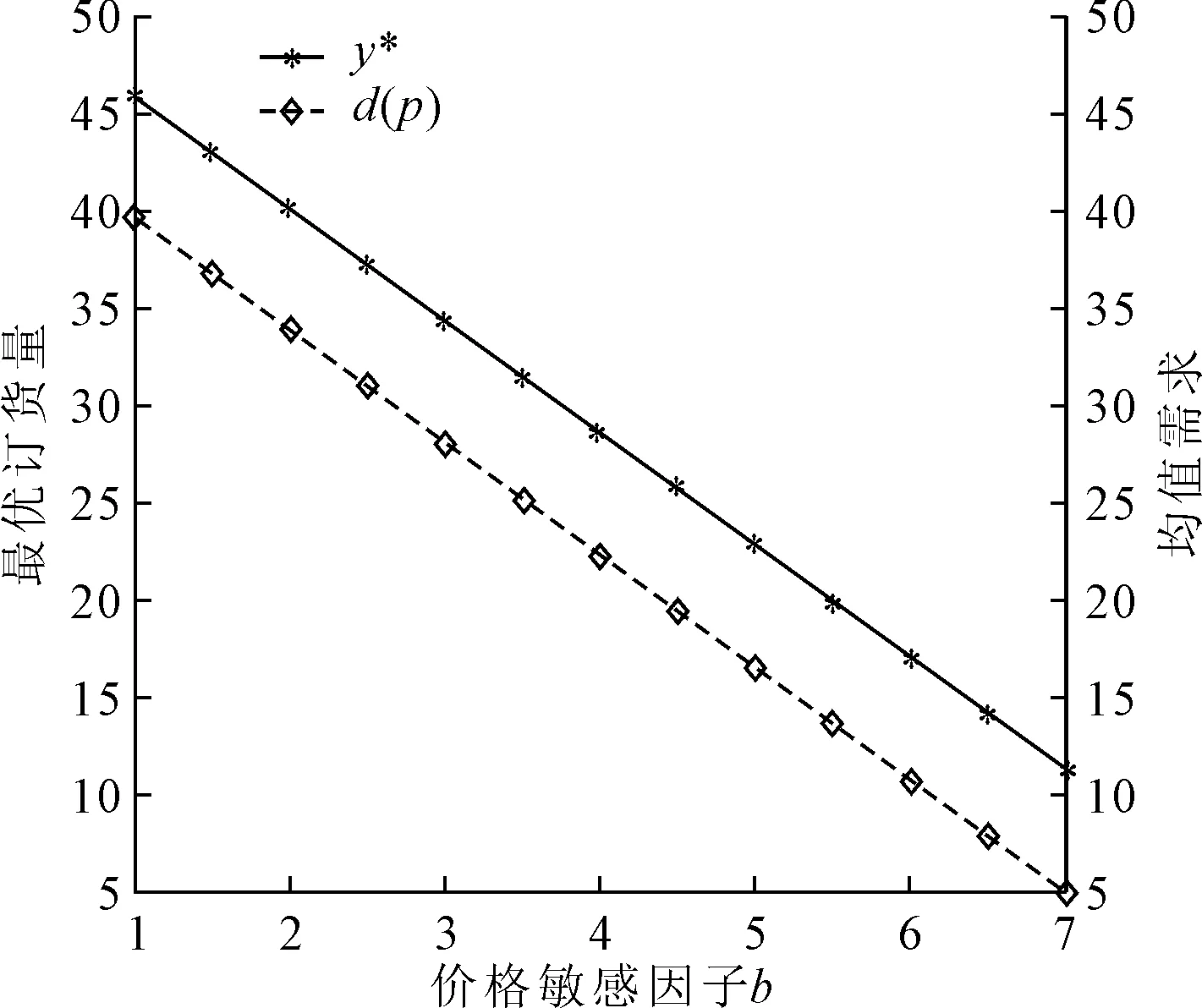
图2 加性需求模式下b对最优订货量y*及均值需求d(p)的影响

而无论是最优销售价格的降低还是最优订购量的减少，均会造成零售商期望利润的损失，加性需求模式下b对零售商期望利润的影响如图3所示，可以看出期望利润随价格敏感因子的增大呈现出下降趋势。

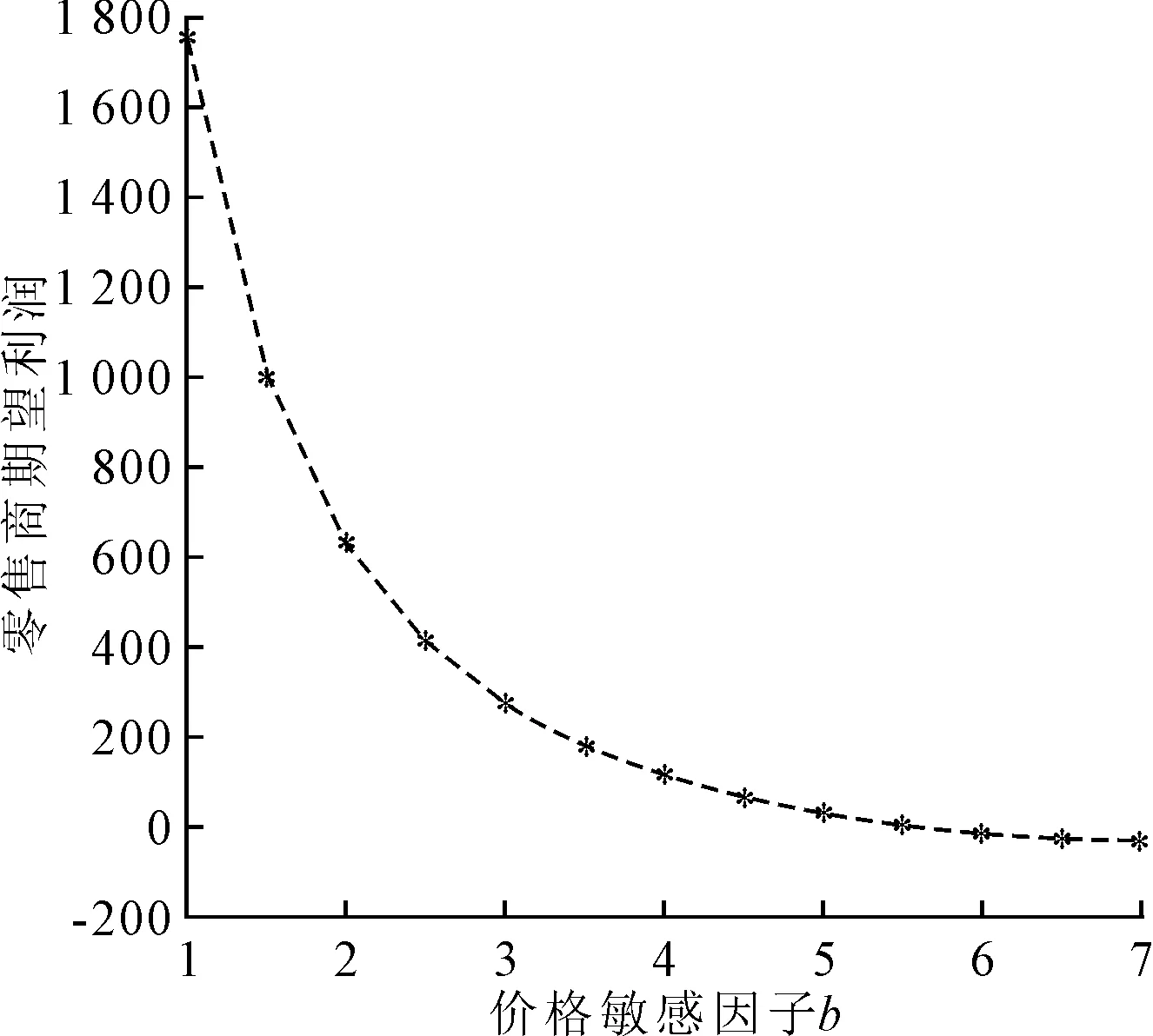
图3 加性需求模式下b对零售商期望利润的影响

(2)针对乘性需求模式，假设ε服从正态不确定分布N(120,4)，保持参数a=10 000、q=11.5、h=7.6不变，令价格敏感因子b从1.1到1.8变化，探讨价格敏感因子对零售商最优决策和期望利润的影响。其中，乘性需求模式下b对最优销售价格p*的影响如图4所示，可以看出最优销售价格p*随价格敏感因子b的增大而减小，最终趋于稳定，但相较于加性需求模式，乘性需求模式下的最优销售价格对价格敏感因子的反应更为灵敏。

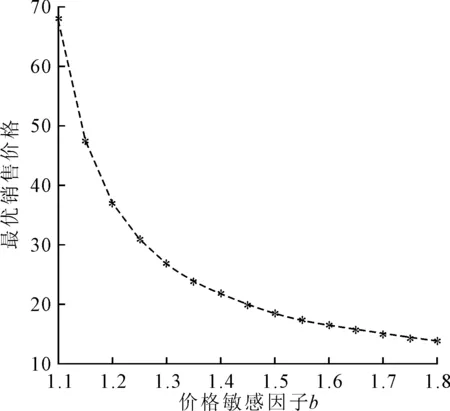
图4 乘性需求模式下b对最优销售价格p*的影响

乘性需求模式下b对最优订货量y*及均值需求d(p)的影响如图5所示，可以看出乘性需求模式下，最优订货量y*、均值需求d(p)均随价格敏感因子b的增大呈现先增大后减小的趋势，这说明价格敏感因子b较小(b<1.3)时，价格降低导致的均值需求增加量超过价格敏感因子增大导致的需求减少量。此时，零售商倾向增加订货量来弥补价格降低引起的期望利润损失。而价格敏感因子b较大(b>1.3)时，价格受成本限制而逐渐稳定，此时零售商无法通过降低销售价格来减轻价格敏感因子增大带来的市场需求量损失，最终导致均值需求下降，此时零售商订货量呈现下降趋势。

图5 乘性需求模式下b对最优订货量y*及均值需求d(p)的影响

结合图4和图5可知，虽然最优订货量y*随价格敏感因子b先增大后减小，但提高订货量带来的期望利润增加小于降低销售价格引起的期望利润损失，因此零售商期望利润整体随价格敏感因子的增大而减小，如图6所示。

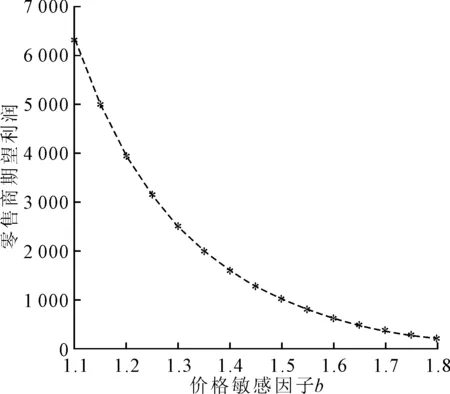
图6 乘性需求模式下b对零售商期望利润的影响

4.2 市场需求扰动项方差对零售商最优决策和期望利润的影响

鉴于篇幅原因，笔者仅对加性需求模式下市场需求扰动项方差σ2对零售商最优决策和期望利润的影响进行分析。保持其他条件不变，令σ2在(4,64)内变化，加性需求模式下σ2对最优销售价格p*的影响如图7所示，可以看出当价格敏感因子保持不变时，市场需求扰动项方差σ2对最优销售价格p*没有显著影响，且价格敏感因子b越大，最优销售价格p*越小。

图7 加性需求模式下σ2对最优销售价格p*的影响

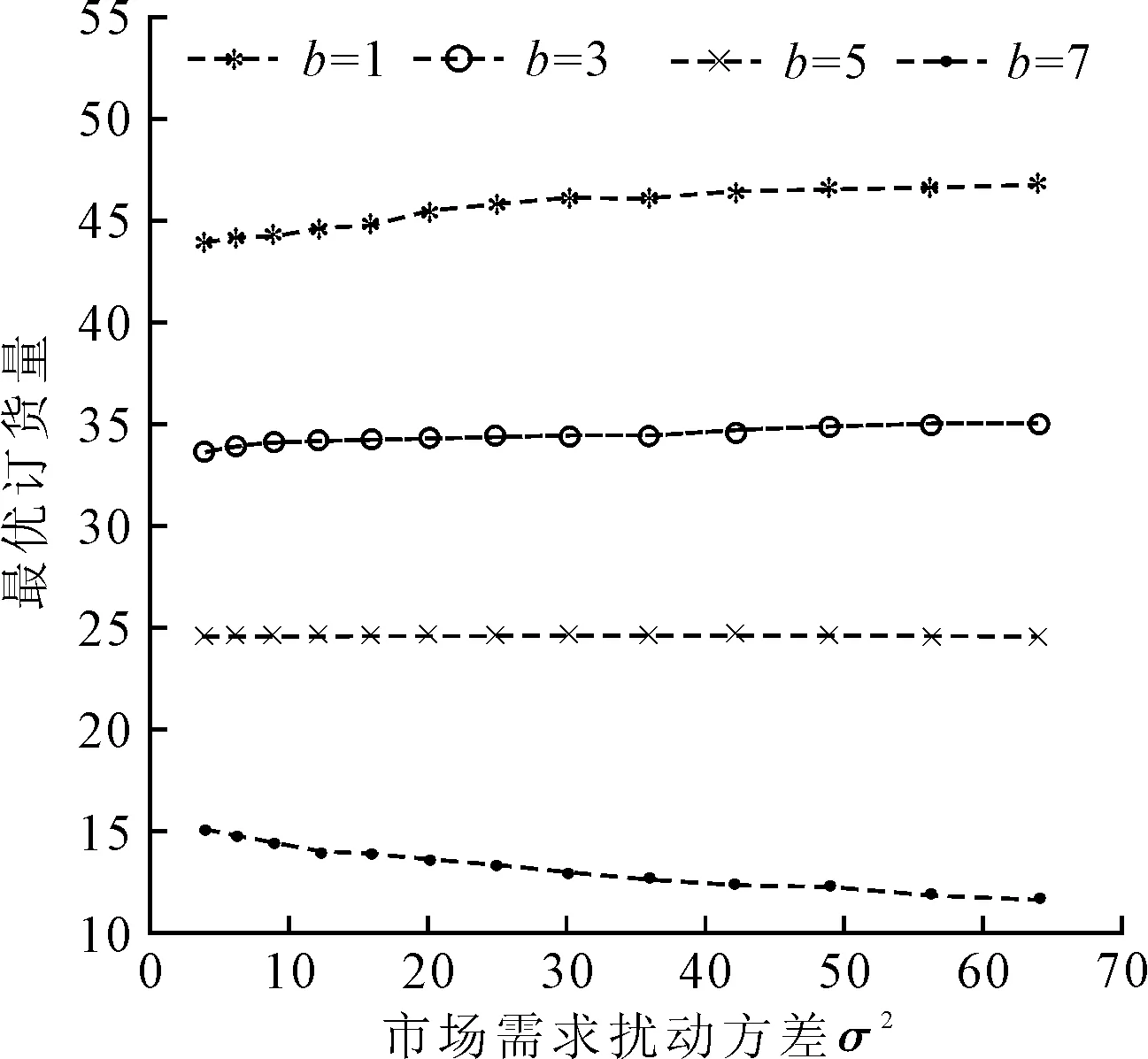
图8 加性需求模式下σ2对最优订货量y*的影响

加性需求模式下σ2对最优订货量y*的影响如图8所示，可以看出不同的价格敏感因子下，随着市场需求扰动项方差σ2的增大，最优订货量y*呈现不同的变化趋势。当价格敏感因子较小(b<3)时，最优订货量y*随着σ2的增大而增大。这是因为当价格敏感因子较小时，产品销售价格受价格敏感因子的影响较弱，零售商会保持较高的销售价格。随着σ2的不断增大，市场需求随机波动性增强，但较高的销售价格导致的零售商缺货机会成本的提升，远大于市场需求降低带来的库存积压风险，即σ2的增大所带来的正面效益高于负面影响，因此零售商倾向制定高订货量决策。而当价格敏感因子较大(b>5)时，最优订货量y*随着σ2的增大而减小。这是因为当价格敏感因子较大时，零售商的最优销售价格降低，零售商利润空间被压缩，此时随着市场随机波动性的不断增强，零售商更倾向降低订货量来弥补期望利润损失。

加性需求模式下σ2对零售商期望利润的影响如图9所示，可以看出虽然市场波动对价格的影响不大，但市场需求随机波动性的增强会增加零售商运作成本和缺货机会成本，导致零售商期望利润的整体降低，即零售商期望利润随着σ2的增大呈现下降趋势。

图9 加性需求模式下σ2对零售商期望利润的影响

5 结论

笔者针对不确定市场需求，运用不确定理论，分别在加性需求模式与乘性需求模式下，研究了零售商最优定价与订购联合决策问题，验证了市场需求为不确定变量时零售商最优决策存在的充分条件和表达式，并通过数值分析探讨价格敏感因子和市场需求扰动项方差对最优决策和期望利润的影响。

研究结果表明：①加性需求模式下，零售商最优销售价格、最优订货量随价格敏感因子的增大而减小，即价格敏感因子越大，零售商越倾向低销售价格和低订货量的联合决策，以降低不确定需求带来的风险。②乘性需求模式下，最优销售价格随价格敏感因子的增大而降低，而最优订货量随价格敏感因子的增大呈现先增大后减小的趋势，说明价格敏感因子较小(b<1.3)时，零售商倾向采取低销售价格和高订货量的联合决策；而价格敏感因子较大(b>1.3)时，零售商更倾向制定低销售价格和低订货量的联合决策。③市场需求扰动项方差对零售商最优销售价格的影响并不显著，但当价格敏感因子较小(b<3)时，最优订货量随着市场需求扰动项方差的增大而增大，当价格敏感因子较大(b>5)时，最优订货量随着市场需求扰动项方差的增大而减小，且零售商期望利润随着市场需求波动性的增大呈现下降趋势。因此对市场随机波动性情况做出正确预测，调整最优定价及订购决策，对零售商降低企业风险和维持期望利润具有战略意义。

综上，笔者应用不确定理论，将不能得出准确发生频率及分布函数的市场需求假设为不确定变量，而非随机变量，并对其进行不确定建模处理，弥补了概率论建模的局限性，为零售商提供了联合定价及订购决策的理论依据。但笔者只讨论了零售商面对不确定需求的定价与订购联合决策时的基本模型，未涉及不确定环境下供应链其他成员的最优决策，而随着供应链一体化的不断发展，供应链上下游任何企业的决策均会影响渠道整体效益，因此不确定需求下供应链决策及协调机制将是今后的研究方向。