吉他d弦不同弹拨位移下振动特性及声学品质

文/矫盼盼 袁威 庄桥

（山东建筑大学理学院 山东省济南市 250100）

音乐声学是一个具有挑战性的研究领域，在许多方面推动着声学的发展。Fletcher和Rossing回顾了对西方乐器研究的发展[1]；Legge和Fletcher通过理论和实验方法，研究了吉他琴弦不同频率振型间能量的非线性传递[2]；Richardson和Roberts提出了时均全息测量法研究吉他顶板在低频模式下的典型模态形状[3]；Woodhouse研究了几种不同的方法来分析吉他的拨动反应[4]；郑林启分析了吉他弦振动频谱与弹拨弦力度之间的关系[5]。吉他是一种拨弦乐器，琴弦作为琴码和共鸣箱的激励结构，对吉他的声学特性有着重要影响。目前对于由不同弹拨位移引起的吉他弦振动特性的研究较少，本文介绍了一种分析吉他琴弦的振动特性和声学品质的方法。

1 理论

1.1 拨弦时吉他弦振动动力学分析

在外力作用下弦上各点的位移满足经典物理的弦振动偏微分方程[6]：

弦的横振动方程的解为：

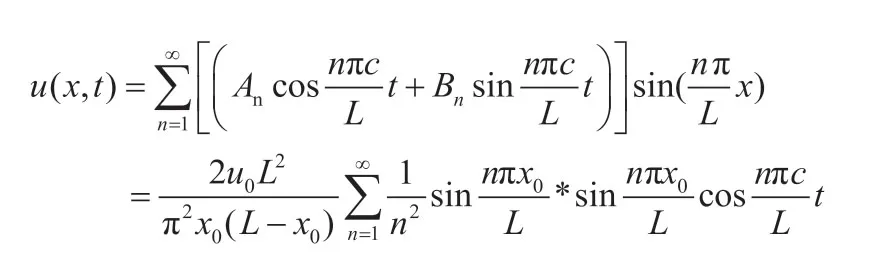
1.2 基于圆形霍夫变换的图像处理算法

为了追踪标记点的运动轨迹，采用基于梯度的圆形霍夫变换图像处理算法自动提取标记点的几何中心位置。霍夫变换根据待识别目标的形状函数来定义从图像点到累加器空间的一个映射。对于圆形目标，圆的方程和映射根据以下公式进行运算[7]：

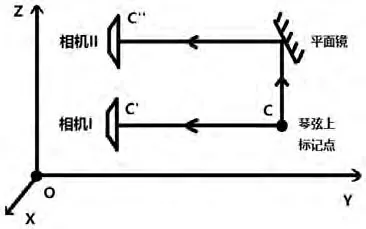
图1：双相机非接触式光学测量系统的光路设计

图2：局部放大拍摄的实验图

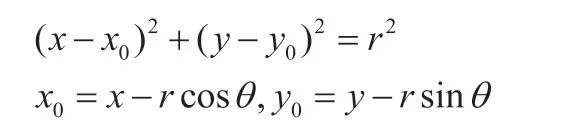
其中(x,y)表示一个点的位置坐标，(x0,y0)表示圆的原点，r是圆的半径，θ是圆心角。在进行圆形霍夫变换之前，先用以下方程计算预处理图像的梯度场：

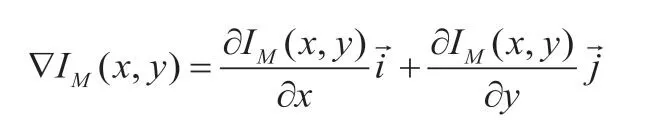
2 实验方法

为了测量吉他拨弦过程中琴弦的振动情况，在光学平台上搭建了一个双相机非接触式光学测量系统。根据图1的光路设计，在琴弦上设置标记点C，相机I可以直接拍摄点C在X-Z平面的振动（相机I中点C'），点C在X-Y平面的振动则通过光路变化传递到相机II中点C''，通过两台相机同步拍摄两个平面内的振动情况。

实验采用德国pco.1200s高速相机，拍摄速度为501-32023帧/秒，画面像素高达1280×1024，可通过自行定义拍摄区域及调整放大倍数进行局部显微放大拍摄（图2），实验中高速相机拍摄速度为3600帧/秒，图片分辨率为200×56。使用圆形霍夫变换图像处理算法对每帧点C的位置进行追踪，得到点C中心位置坐标，图像比例可通过比例尺标定。

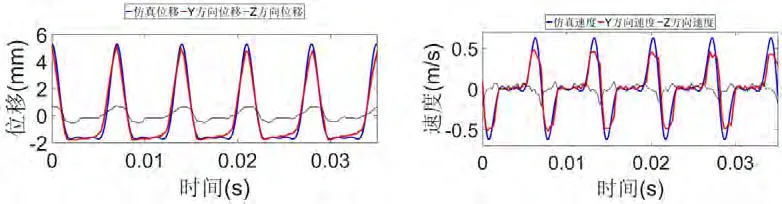
图3：d弦的振动位移和振动速度

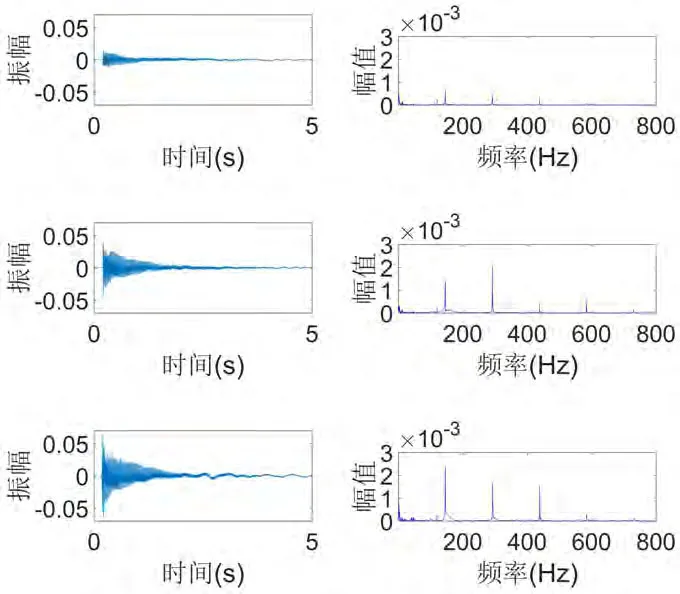
图4：d弦在不同弹拨力度下波形图和频谱图

实验前对吉他进行空弦基频校准，d弦空弦基频为146.8Hz。使用拉力计定量琴弦初始位移，对琴弦进行不同弹拨位移的拨弦实验，同时通过AWA6228+型一级声级计采集不同弹拨位移下吉他琴弦振动的声信号。

3 结果和讨论

图3为吉他d弦仿真振动位移、速度及Y、Z方向的实测振动位移、速度。

将点C的实测振动位移、速度与仿真振动位移、速度对比发现，Y方向为弹拨位移主方向，与理论符合良好，而Z方向受琴弦与琴码、琴体之间的耦合振动影响，与理论存在偏差。

图4为吉他d弦在弹拨位移分别为2mm、4mm和5mm时的波形图及频谱图，由于第五谐音以上人耳已不易听见，因此本次实验只研究第一谐音至第五谐音。

随着弹拨位移的增大，波幅逐渐增大，响度逐渐增强，第二、三、四次谐音成分增加，声音的亮度增加，听起来更为清晰；第五谐音成分明显增加，音色逐渐浑厚。

4 总结

对吉他琴弦的振动位移和速度进行了理论和实验分析，实验结果与理论符合良好。分析了吉他琴弦在不同位移下的谐波成分，为吉他的结构设计和品质控制提供了一种评估方法。本文只分析了吉他弦振动与弹拨位移的关系，进一步的研究包括琴码和共鸣箱材料对吉他振动特性和声学品质的影响。