基于克强指数的苏州地区工业发展建议
韩 月,杨云霞,周凌轲
(江苏科技大学 苏州理工学院 商学院,江苏 张家港215600)
克强指数是基于经济发展的“工业用电量”“铁路货运量”“银行中长期贷款”这三个指标。2010 年,英国著名杂志《经济学人》将上述三个指标予以综合带入一个具体公式,创造出一个新的衡量GDP 增长的指标,称为“克强指数”(克强指数=工业用电量增速×40%+中长期贷款余额增速×35%+铁路货运量增速×25%)。该指数自从被推出后,就受到多家权威性国际机构认可,因其客观公正性,地方政府几乎无法干涉,不易作假,使得记录的数据更为真实可信,能更真实地反映经济运行状况(田明静)。
一、研究方法与数据来源
在“克强指数”被提出后,很多学者运用它对我国经济进行分析预测,得出了大量结论。叶允最在建立广西工业总产值和修正后的“克强指数”的关系实证模型的前提下,对其进行了实证分析,证实它们之间存在长期均衡关系并提出相应政策建议。周业付等人运用协整理论等分析“克强指数”对上海经济发展的影响,提出应扩大上海开放程度,尤其是加快自贸区建设的思路。刘帅等人通过构建新克强指数与青海经济增长的差分模型,揭示了金融服务对青海经济发展贡献有限,科技投入不足的问题,提出应大力引进高技能、高层次人才的对策措施。但至今为止,仍较缺少以“克强指数”来研究苏州发展的成果。本文在“克强指数”的指导下对苏州工业总产值、工业用电量、货运量和中长期贷款进行回归分析,基于分析结果,力图为苏州地区的经济发展提出政策性建议。
因为“克强指数”是李克强总理当初针对辽宁省的经济状况而做出的一个指标,所以“克强指数”可以很好地反映辽宁省及其产业结构和发展状况相似的省份的经济状况(唐德祥)。但对其他一些发展差异较大的区域,如对苏州进行研究时就有必要作一定的调整。如解释变量的选择,本文一是以苏州实际工业用电量为据。二是以苏州总的货运量为主,包括公路、水路、铁路运输。因为苏州处于长江三角洲中部,太湖东岸,公路运输和水路运输在工业货运量中的比例远高于铁路货运量,不容忽视,故做出此调整。三是以银行中长期贷款总量为主。
在模型设定方面,采用C-D 函数双对数模型形式建立模型:lny=c+β1lnx1+β2lnx2+β3lnx3。在模型中,y为工业总产值(亿元),x1为工业用电量(亿千瓦时),x2为货运量(万吨),x3为中长期贷款(亿元),c 为随机误差项,以2014 年1 月为基期,数据采用2014年1 月—2019 年8 月的《苏州统计年鉴》和《苏州统计月报》。
二、“克强指数”因素与工业总产值关系分析
(一)WLS 回归估计结果
运用上面的数据(实际参数为58 个,因原数据中部分月份中长期贷款额为负,无法进行对数及数据免报问题,故剔除)。利用Eviews 采取加权最小二乘法对“克强指数”因素与苏州工业总产值之间进行时间序列分析,为消除异方差问题,权重使用残差绝对值的倒数(w=1/abs(resid))。可得如下估计结果,全部变量均通过显著性水平检验,但中长期贷款C 值为负,猜测可能因为中长期贷款量为滞后指标,它对工业总产值的作用具有一定的滞后性,所以苏州的中长期贷款无法在当期对工业总产值产生作用,因此有必要进一步检验在t-n 期投入的中长期贷款能否对当期工业总产值产生效用。
故分别将t-1 期,t-2 期,t-3 期的中长期贷款数据代入当期数据中,进行三次回归分析可知,t-1期,t-3 期中长期贷款分析结果均在5%显著性水平下拒绝原假设,只有t-2 期中长期贷款分析结果通过检验,并得到良好的结果。说明当期进行的中长期贷款会在两期之后对工业总产值产生影响,具体分析结果如表1。
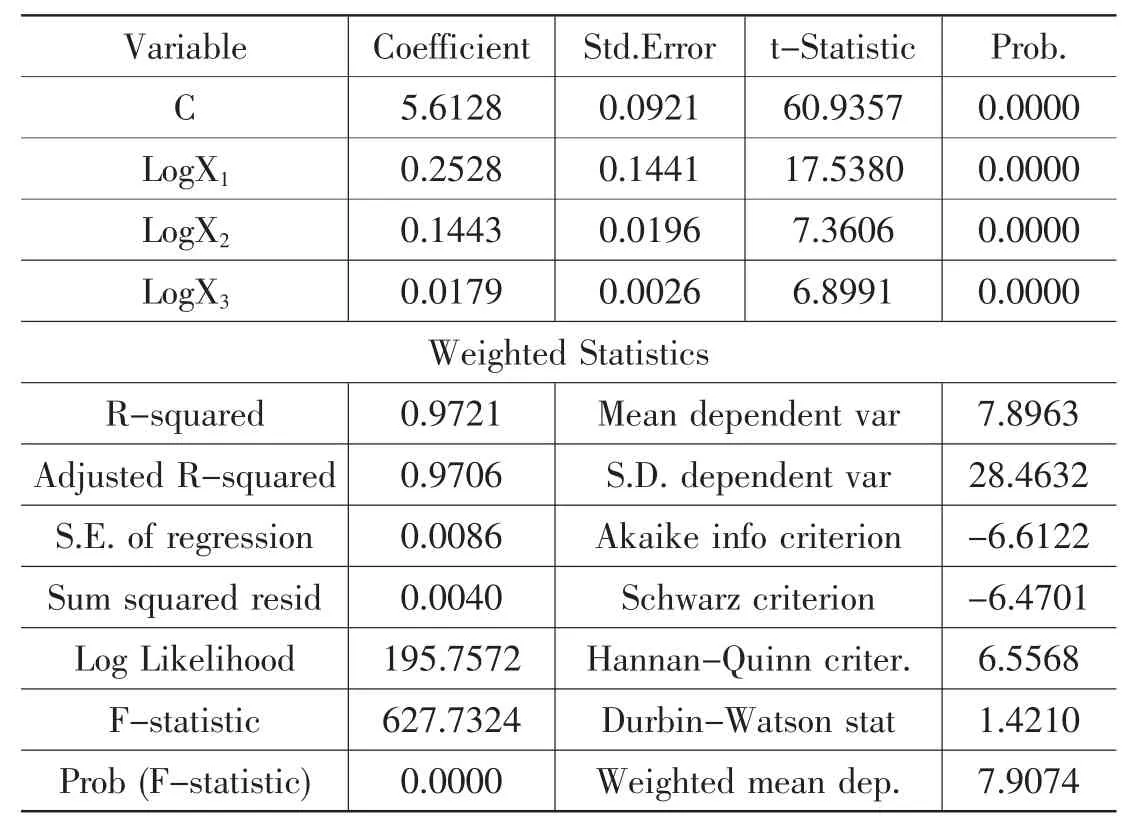
表1 t-2 期中长期贷款下加权最小二乘法回归分析结果
由表1 可知,判定系数R2=0.972125,几乎接近于1,这三个影响因素解释了苏州工业总产值变化的97.2125%,说明所建立的模型对于样本数据的拟合优度比较高。lny 和变量 lnx1、lnx2、lnx3均通过 5%显著性水平检验,F=627.7324,大于临界值,顺利建模。研究表明,克强指数在苏州其他变量不变的条件下,当工业用电量每增加1%就会引起工业总产值增加0.253%,当货运量每增加1%,工业总产值将会增加0.144%,当中长期贷款每增加1%,工业总产值将会增0.018%,对苏州GDPuttg 重大影响。
(二)自向量回归估计结果
通过一阶差分变化得出模型结果如下:AIC=-2.759957,SC=-2.609861;二阶差分变化得出的模型结果如下:AIC=-1.690136,SC=-1.531124
用 AIC 准则 (Akaike In.f0 Criterion) 和 SC准则 (Schwarz Criterion) 确定最优滞后阶数(Lagged differences)为一阶。
(三)基本检验
1.本文采用ADF 单位根检验方法,对变量lny、lnx1、lnx2和 lnx3的差分序列进行平稳性检验,由此确定序列的平稳性,检验结果为经过二阶差分的lny、lnx1、lnx2和 lnx3均在 1%显著水平下成立。因此,4 个原始序列都是二阶单整序列,满足同阶单整条件,可用于协整分析。
2.本文采用Johansen 检验法对选取的变量进行协整关系检验,以研究克强指数各指标与苏州工业发展的长期均衡关系,由不存在协整关系的原假设开始,直到存在四个协整关系时,迹统计量均在5%的显著性水平下大于5%的临界值,即拒绝原假设,说明这四个指标与苏州工业总产值有长期稳定的均衡关系。
3.本文采用Granger 因果进行检验,根据检验结果可以得知,在10%的显著性水平下,苏州市工业总产值与货运量和中长期贷款量不具有因果关系,而工业总产值和中长期贷款量是工业用电量的Granger 原因,工业用电量对苏州工业总产值起到明显作用(见表2)。
四、结论与政策建议
中长期贷款存在滞后期,滞后期长短取决于该区域的金融业发展水平,金融业发展水平越高,则滞后期相应越短,苏州的中长期贷款滞后期为两个月,说明其经济发展水平较高。苏州市经济一直位于全国前列,国家对苏州市经济发展也较为扶持,但中长期贷款对苏州工业总产值的影响较小。可能是因为近年来苏州市贷款用途多样,投资结构也在不断优化调整,截至2018年,苏州市全市服务业增加值占地区生产总值比重达到50.8%,经济发展逐步由依靠能源消耗的第二产业转向依靠科技发展的第三产业。苏州市要实现进一步的发展,就需要深化投资领域改革、推动贸易转型升级、深化金融领域开放创新、推动创新驱动发展,着力规划建设苏州自贸区,促进苏州市经济发展。
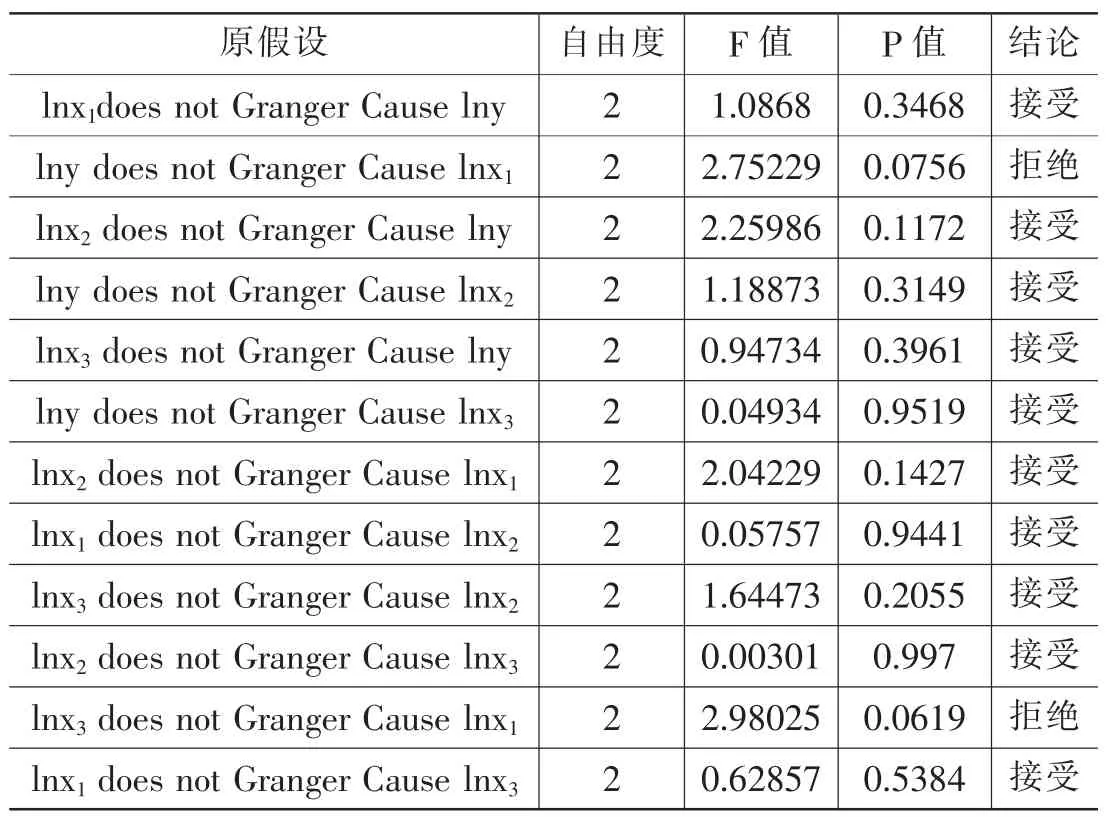
表2 Granger 因果关系检验结果
苏州工业总产值增长对用电总量有很强的依赖性,且在Granger 因果检验中,工业用电量对苏州工业总产值起到明显作用。因为现阶段的苏州工业总产值增长都是基于高增长的工业用电量,虽然极大地推动了工业总产值,但同时也带来了能源的消耗和污染问题。在苏州经济发展新常态下,必须要重视改进产业结构,淘汰一批高消耗、高污染、低产值的落后企业,依靠苏州的高等教育和科技研发优势,推动发展和扶持互联网、纳米材料、人工智能等高端产业,逐步形成低污染、高产值的产业结构。在保持GDP 高增长的同时,降低对能源资源的消耗,培养我国自己的高端企业,发展尖端技术,积极开发新绿色环保能源,减少石油、煤炭等高污染能源的使用。特别是充分利用苏州“十三五”规划,重点发展高炉煤气、焦炉煤气等资源综合利用发电项目,全面推动、指导苏州市现有钢铁企业等重工业企业开展节能技术改造,发展循环低碳经济,促进工业经济转型升级,提高能源资源利用效率,与国家的供给侧改革相呼应,为苏州经济可持续发展提供可靠保障。
苏州市货运量对苏州市工业总产值有较大的贡献度,2018 年全市公路、水路货运量1.62 亿吨,货物周转量267.82 亿吨公里,分别比上年增长8.2%和7.3%;苏州港集装箱吞吐量635.51 万标箱,比上年增长8.2%。尤其是在对外贸易中,全年实现进出口总额3541.1 亿美元,比上年增长12%。其中出口突破 2000 亿美元,达 2068.3 亿美元,增长10.5%。苏州位于太湖之滨,长江南岸的入海口处,多条高速公路贯穿全境,所以应利用水运和陆运的天然优势,同时加快交通运输业的基础设施建设,形成更加完善高效的国际运输体系。尤其是着力于一带一路沿线铁路建设,进一步调整优化苏州对外贸易结构,推动苏州工业园区与新加坡合作参与“一带一路”建设,积极主动参与国家“一带一路”开发,加快本土企业“走出去”步伐,提高苏州本土企业的高新科技产品在新兴国家市场的占有率,带动苏州市工业总产值的增长,促进苏州经济发展。

