基于STM32单片机驱动的双液体棱镜

胡思哲，葛 屹，邓天豪，张 谦

(重庆大学 电气工程学院，重庆400044)

1 引 言

光束偏转技术广泛地应用于激光雷达、通信、光存储等领域[1]。然而传统的光束偏转技术依托于机械装置改变光轴方向来实现光束的偏转，装置存在体积庞大、结构复杂、维护成本高、能耗高等缺点，并不符合现代光电系统便携化、低功耗的要求。

近几年出现的基于电润湿原理的微流控光学器件，利用改变液体界面润湿角的原理实现光束偏转控制，具有结构简单、制作简便、易于集成、响应速度快的优点[2]。2011年，辛辛那提大学的Hou[3]提出了基于电润湿效应的双液体棱镜理论，实现了光束偏转的控制，为微流控光学器件的实用化进一步提供了依据；Lin[4]等人通过制备三液相的电润湿棱镜实现了折射角控制范围的进一步扩大；Cheng[5]提出通过电润湿液体光学器件实现太阳聚焦的功能，将基于电润湿的光学器件应用到了更广阔的范围。但是目前对于微流控光学器件的研究主要集中于介电润湿材料性能的分析，对于外施加电控系统的设计相对较少，即如何实现电控系统与单元化器件的集成，让装置的体积相对较小，应用环境更广。

本文设计了一款基于STM32单片机的可调电润湿双液体棱镜装置，通过升压斩波电路输出4路可调直流电压，使棱镜器件与电控系统集成化，实现了棱镜对于入射光束转向的二维连续控制，并通过Comsol软件仿真验证了模型的正确性。

2 电润湿双液体棱镜原理

电润湿效应是通过改变液体与接触基板之间施加的电压，达到改变其在基板上的润湿性，使接触角发生改变，液滴发生形变或位移[6]。在实际应用过程中，通常会在基板上涂覆介质层与疏水层，即基于介质上的电润湿(Electrowetting-on-dielectric)，介质层的引入可以尽可能地消除电解的发生。Young-Lippman方程描述了接触角与外加电压之间的关系[7]：

(1)

式中:θ0是液滴在疏水表面的初始接触角；θv对应施加电压后的接触角；d、ε0、εr分别对应介电层厚度、相对介电常数与真空绝对介电常数；γ代表液体界面处的表面张力;V代表外施加电压。

基于电润湿原理的双液体棱镜如图1所示。棱镜采用长方体结构，在导电侧壁上涂覆透明的绝缘介电层与疏水层，腔体内部装入两种不相溶的透明液体，下层为低折射率的导电NaCl溶液，上层为高折射率的绝缘非极性硅油，两种液体的密度需较为相近，以保证模型结构不受方位的影响。

通过对液体棱镜的4个侧壁分别施加电压，4个侧壁对应的接触角将被电压控制，并依据Young-Lippman方程变化，实现了对于光束的二维控制。当侧壁不施加电压时，液体棱镜液面呈现自然的弯曲形状如图2(a)所示。为了使棱镜液面呈现平面倾斜的状态，要求相对的2个侧壁(左侧壁、右侧壁)分别施加电压VL、VR后接触角满足θL+θR=180°(其中θL代表左侧壁接触角大小，θR代表右侧壁接触角大小)，即满足以下关系式：

(2)

(3)

另一对侧壁的接触角满足均为90°时，棱镜液面呈平面倾斜的状态，且倾斜程度跟随着施加电压变化，如图2(b)所示。

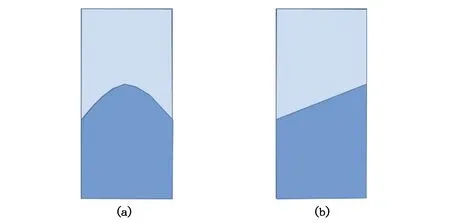
图2 液体棱镜侧壁。(a)液面自然弯曲；(b)液面平面倾斜。

当入射光线从空气垂直入射到绝缘油与导电液体界面时，由于两种液体的折射率不同，光线发生第一次折射，此时入射角为α，折射角为β。当光线从导电液体界面再次射入空气时，会发生二次折射，此时入射角为γ，折射角为δ，出射光线与垂直入射之间的角度偏差即光线的偏转角，如图3所示。

图3 入射光线偏转示意图

根据斯奈尔定律，可得偏转角与各介质折射率及接触角的关系[8](式中noil为绝缘油的折射率；naqueous为导电液体折射率)：

(4)

(5)

基于电润湿效应，当外界对棱镜的侧壁施加不同大小的电压时，两种液体界面的接触角发生相应改变[9-16]，且遵守Young-Lippman方程。并且可以确定棱镜偏转角的大小取决于接触角与液体与空气介质的折射率，关系如式(6)所示：

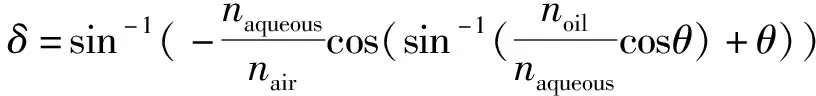
(6)

当接触角变化时，棱镜的偏转角随之变化，但由于疏水涂层材料选择不同以及接触角饱和现象[2]的发生，施加电压下接触角变化范围有限，故棱镜的最大偏转角会受到相应限制。

3 双液体棱镜电控系统设计

3.1 电控系统工作流程

控制系统的原理框图如图4所示。用户预设的横向倾角和纵向倾角数值通过单片机控制模块的人机交互模块输入。经过控制算法的处理，得到液体棱镜的4个侧面分别应该施加的电压幅值，再根据4个幅值分别输出4路占空比不同的脉冲宽度调制(Pulse Width Modulation，PWM)波给单相移相调压模块，使4个调压模块以及整流电路将由交流稳压电源提供的220 V电压转化为液体棱镜4个侧面所需要的电压。

图4 电控系统工作原理图

3.2 电路结构具体构成及各部分原理

3.2.1 单片机控制系统

用于输出PWM信号的单片机控制系统以意法半导体公司的32位ARM微处理器STM32F103为核心，选用12 MHz晶振组成时钟电路，与复位电路、电源输入电路和PWM驱动电路一起组成。控制系统的原理图如图5所示。

PWM驱动电路主要是将STM32F103输出的幅值为3.3 V的PWM信号通过三极管进行放大以达到IGBT的门限电压，中间使用光电隔离耦合器对单片机和单相移相调压模块进行电气隔离，保护STM32F103芯片不受到意外损害。

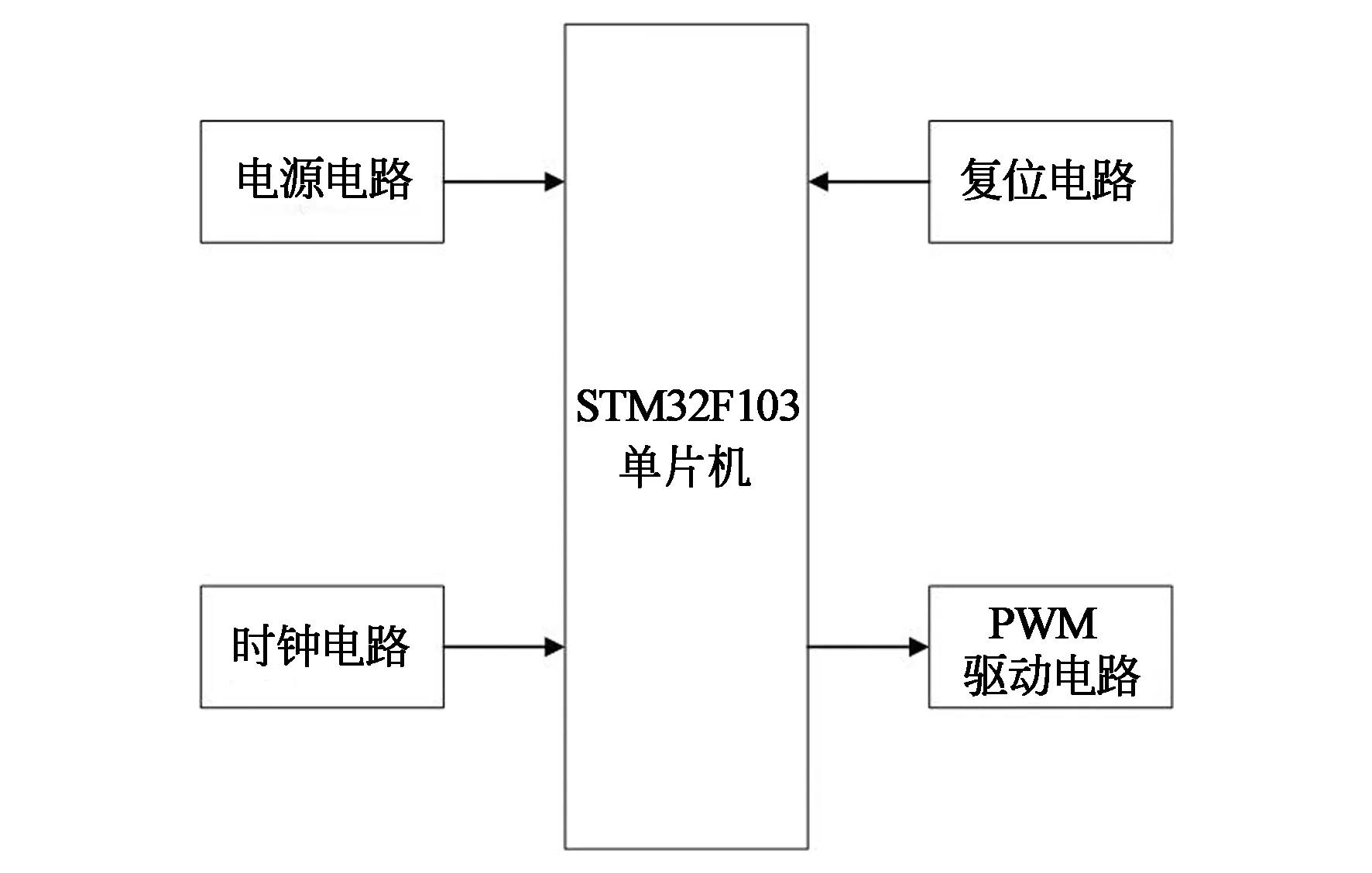
图5 单片机控制系统组成

3.2.2 单相移相调压模块

系统选用LSA-H3P15YB单相交流一体化调压模块与全桥整流电路组成。图6为LSA-H3P15YB的电路连接图，将交流稳压电源的输出端接入模块的1、3口，单片机输出的PWM波接入该模块的CONT控制端，即可从2、4端输出调节后的交流电压。经过全桥整流电路处理后，就得到需要的附加电压。该模块内部集移相触发电路、单向或双向可控硅、RC阻容吸收回路以及电源电路等为一体，无需外接电源，并可在对较高的电网电压进行调节的同时保护可控硅，防止电路过流烧坏可控硅。

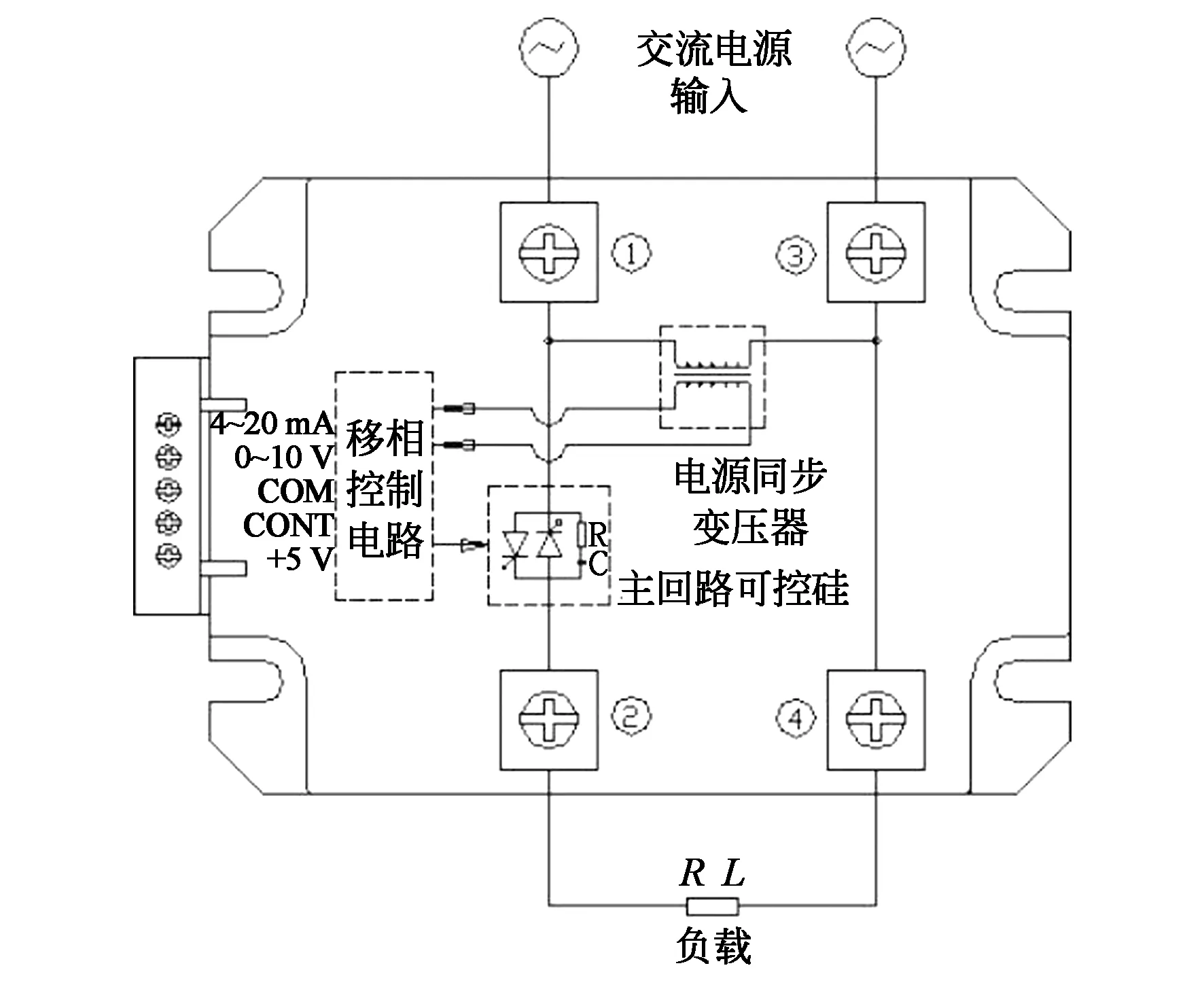
图6 LSA-H3P15YB的电路连接图

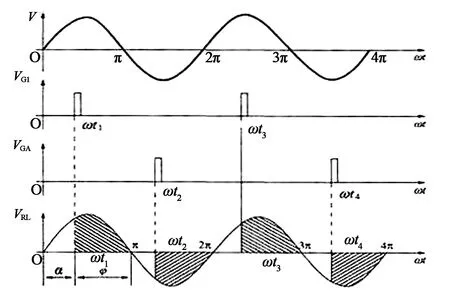
图7 移相触发调压原理

单相移相调压[17-19]模块的基本调压原理是移相触发。移相触发是可控硅(晶闸管)控制的一种方式，它通过调节可控硅的导通角大小来控制可控硅的导通量，从而调节控制输出功率或电压。它的特点是控制波动小，使输出电流、电压能够平滑升降。

如图7所示，V为交流稳压电源输入1、3口的原始电压，单片机输出的PWM波VG1和VG2使可控硅仅在高电平时导通，从而将2、4口负载输出信号VRL每个周期的一部分截止，从而减小了负载输出电压的平均值，实现调压的目的。

输出端使用常见的桥式整流电路进行整流，把交流输出波形整形为控制液体棱镜所需的直流输出波形[20-21]。由于此电控系统采用脉宽调制方式，不改变周期，因此可以避免频率调制易产生干扰的问题。

4 电控系统加压仿真及实验分析

4.1 COMSOL仿真分析

COMSOL Multiphysics[22-23]是以有限元法为基础、通过偏微分方程组的求解来模拟物理情境的一款仿真软件。COMSOL Multiphysics因高效的计算性能、真实可靠的复合场域计算等特点，被运用到工程领域的各个过程中，实现了高精度的数值仿真。

本文采用的软件版本是COMSOL Multiphysics 5.4，通过微流体模块(Microfluidics Moudule)进行仿真。仿真的具体过程可分为5步：选择模块、建立模型、定义参数、移动网格细化和对求解器求解。为了实现对双液体棱镜施加电压这一物理情境的仿真，鉴于已有的输入电压波形分析，此处采用直流高压的方法构成电场[24]。本文的仿真模块选用层流两相流移动网格(TPFMM)，构建出一个10 mm×10 mm×30 mm的长方体物理模型，如图8所示。

图8 双液体棱镜模型

4.2 参数设置

研究的液体变焦透镜的腔体为对称长方体结构，内部填充两种属性的液体：下层溶液设置为导电盐溶液，上层为与盐溶液不相溶的硅油，二者之间初始界面关系满足贝塞尔二次曲线[10]。两种溶液的物理参数如表1所示。NaCl导电盐溶液的密度为1 000 kg/m3，折射率为1.3,动力黏度为2.7×10-3Pa·s；硅油的密度与NaCl盐溶液相匹配，为1 000 kg/m3，折射率为1.65，动力黏度系数为1.3 Pa·s。

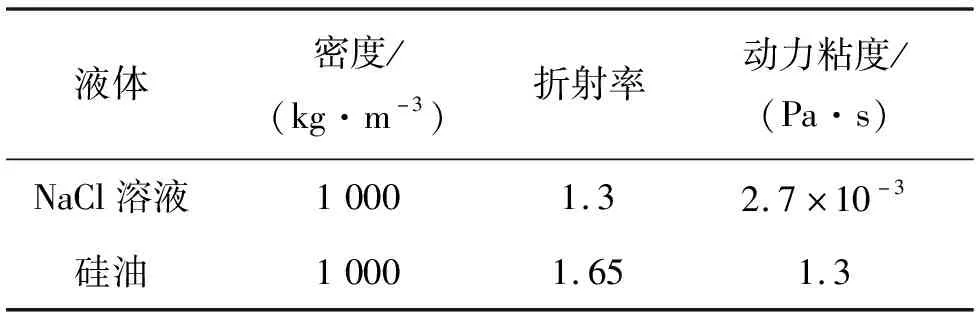
表1 液体参数设置

通过COMSOL Multiphysics建立基于电润湿效应的双液体透镜的物理模型，需要设定其界面面形与施加电压值的关系。由于两种液体之间接触角需满足Young-Lippmann方程，故设置接触角与其他物理参数的关系式，如上述公式所示(单位为rad)。在运算过程中所代入的相关变量参数值，如表2所示。

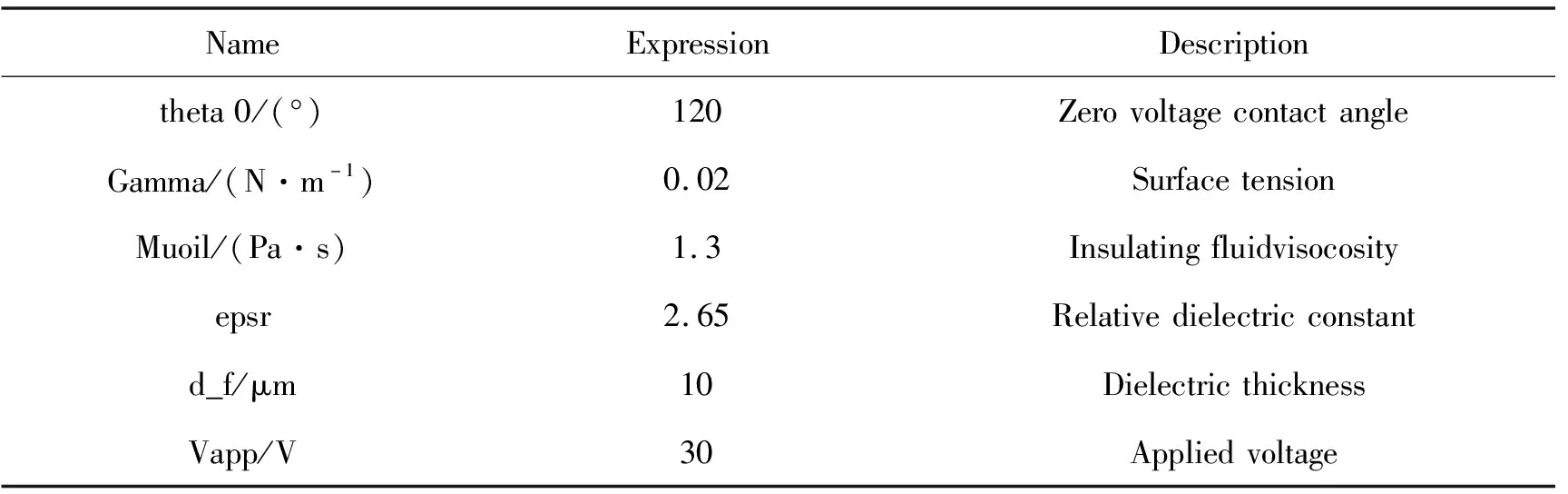
表2 物理参数设置

通过以上步骤完成了长方体双液体棱镜的模型构建，其合理性亦有验证[25]。完成对两相液体的模型参数描述后，通过输入30～160 V范围的电压，可以观察到两相液体接触界面的变化。由于输入电压值的变化会影响形成界面的效果，仿真模型重点探讨了施加电压的响应时间与形成平面面形的条件。

4.3 仿真结果及分析

图9采用了三角形网格分析法，通过三角形网格形状拉伸的方式模拟界面的变化情况。由蓝色到红色的变化象征着剧烈程度由缓至急。图9(a)～(d)分别展示了随着时间推移，其仿真网格的具体变化。对比(a)～(c)过程中的网格拉伸，(c)～(d)过程中的网格变化较为微弱，故认定为界面面形的调整基本完成，系统进入稳定状态。通过多组不同电压下的图像比较，可以得到施加电压后界面变化的响应时间。

从图9可得出结论：由施加电压后界面面形变化过程可知，电压越高，液面面形的变化速度越快。在70 V外加电压下可在0.1 s内实现界面弯折，并形成稳定系统。由于双液体棱镜所需侧壁施加电压较高，在实际调节过程中的响应时间可忽略不计。

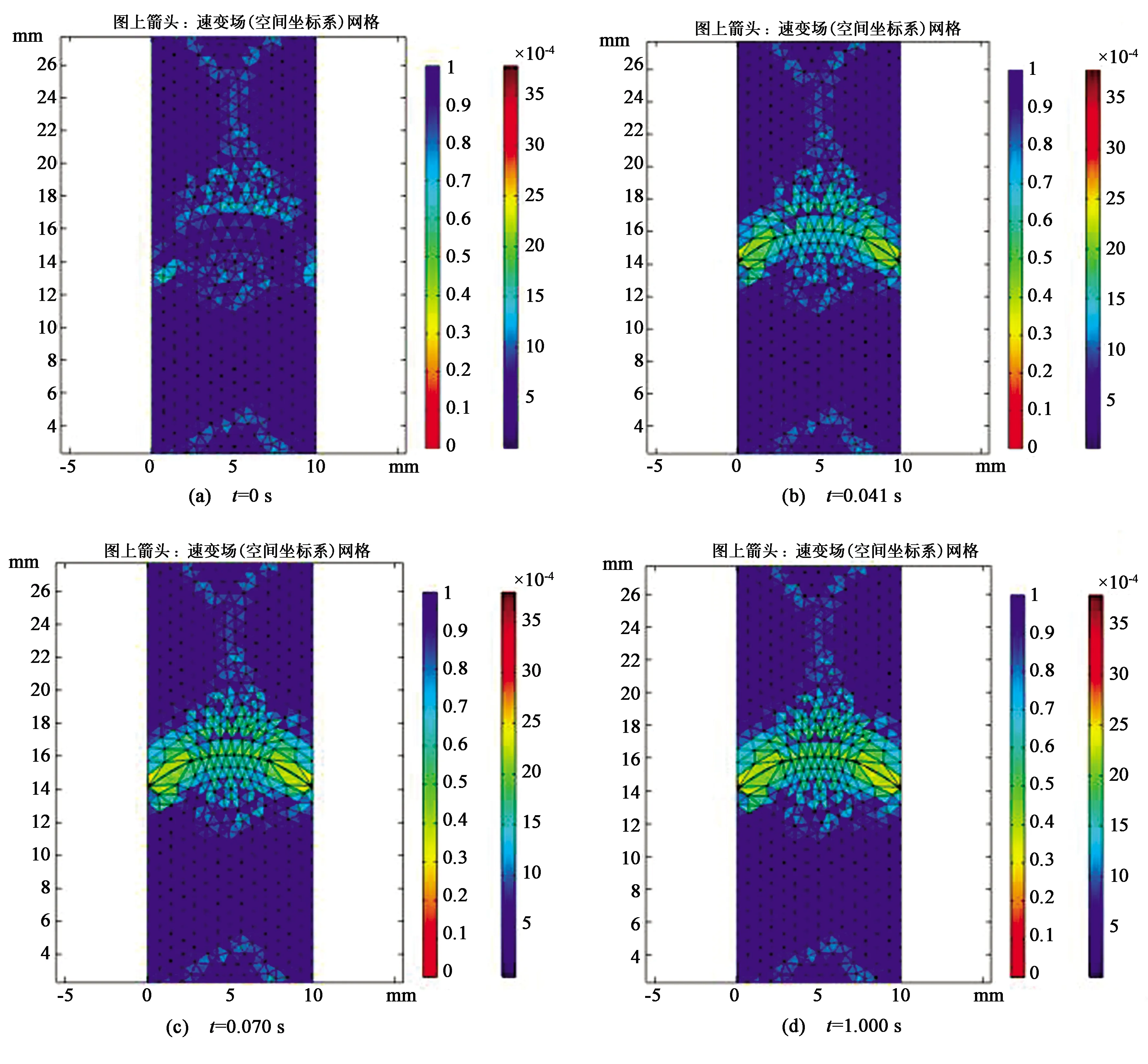
图9 网格分析图

图10 界面面形图

图10给出了特定的双液体界面形状图与相应的侧壁施加电压。从图像可知，图(a)展示了在4个侧壁施加电压均为92 V条件下的界面面形，降低了原界面的弯折程度，使其呈现水平，此时光线的折射效应仅受液体折射属性影响；图(b)显示侧壁施加电压依次为92,92,115，65 V时的两相界面面形，界面呈平面，与两侧壁分别成105°与75°角；图(c)所示为侧壁施加电压分别为92，92，130，5 V时的界面面形，界面呈平面且与两接触侧壁分别成120°与60°角。这一仿真结果也与GLEN等人提出的疏水角变化趋势一致[22]。

通过对图10的分析可以得到以下结论：(1)液体界面面形受到侧壁施加电压的大小影响，随着电压增大，其趋势为从弯向导电溶液侧凹面变为可调平面。可调平面的形成，对于实现两相溶液的折射角度调节具有重要意义。(2)形成实验所需的界面面形，需要保证两侧壁电压为恒值，以便维持平面面形；调节两侧壁的施加电压，可以调节平面与侧壁之间的角度，进而实现折射角的调节。

综上，当输入电路在双液体棱镜侧壁施加4个特定电压时，可形成与侧壁成特定角度的平面界面。COMSOL Multiphysics仿真通过响应时间与界面角关系，验证了该过程的可行性。此状态下，双液体棱镜的折射效果取决于平面与侧壁的夹角，以及两相液体的自身折射系数n。

5 结 论

本文设计了基于STM32单片机的棱镜电控系统，并通过COMSOL仿真软件，实现了双液体棱镜在侧壁施加电压条件下的仿真分析，证明侧壁施加电压后，液面变化的瞬时性。同时通过设置不同输入电压，得到夹角不同的平面面形，验证了调节折射效果的可行性。本文研究的不足在于电润湿棱镜的响应速度还受到施加电压频率、波形的影响，因此，电控系统输出电压的参数设置还需要进一步研究。