水库取水闸门优化调度运行关键技术
王海明,赵平伟,张薇薇
(1. 上海城投原水有限公司,上海 200125;2. 上海城投水务集团有限公司,上海 200002)
21世纪以来,国家更是重视水利工程的建设,水利工程高速发展。水闸作为重要水利工程之一,通过开闭闸门实现引水、拦水、泄洪、排水等重要功能[1-3]。
当今社会,计算机与信息技术高速发展,社会的方方面面都趋向智能化、自动化,在这样的大趋势下,势必要采用新技术、新设备对整个水库的闸门控制设备与管理进行现代化改造,推动水库的智能化建设。由于智能系统在水利工程的发展较快,各个国家的发展也不平衡,现在还缺乏关于水利工程实现智能化系统的统计资料。就国家而言,美国、法国和日本走在世界前列,比较典型的有美国的大古力水电站和日本的玉原抽水蓄能电站。水库闸门智能化控制系统的建立,不但能提高水库信息采集的准确性和闸门控制的灵活性、快速性,而且可以进一步挖掘水库的潜力,提升水库运行的可靠性和安全性,更好发挥水库运行的效益,同时,为上级部门制定防洪抗旱调度方案提供科学依据[4]。
本文中研究的某水库取水闸总净宽为28 m,中孔为通航孔,净宽为14 m,可通航通行疏浚船舶,两侧边孔各7 m。目前正常情况下,水库早上8点左右开闸,边孔闸和中孔闸交替开放,闸门开度约为1.5 m,闸门开启时水位差在1 m以内;晚上10点左右关闸,关闸时库内水位基本和库外保持一致,闸门进水约13~14 h,水位最低在1.9~2.1 m,最高在2.9 m左右。水库的最高水位受来水河流水位的影响,来水河流水位又受太湖水位、闸门下泄流量、潮汐、降雨量等多种因素的影响,且来水河流过往船只较多,来水河流水闸启闭变化频繁。在枯水时期,来水河流的最高水位会降低至2.6 m左右,最低水位会降至2.3 m左右,此时水库进水时间要更长。
换水周期,即水资源的传递更新速率,是湖泊水环境的一个重要参数,影响着水体中污染物与营养物的浓度与停留时间,同时,还会对水体中发生的生物与化学反应过程时间长短造成巨大的影响[5]。换水周期的长短对于改善库区的水质,防止藻类大规模暴发,充分挖掘水库生态系统的自净能力,保障整个水源地的供水安全十分重要。
由于水库方不能提供水闸闸门流速,以及水库库容曲线精度不高,故本文结合数据融合的方法软测量得到水库水量变化方程中的关键变量,闸门流速液位差变化函数曲线与库容变化函数曲线。根据拟合得到的参数与相关数据构建水库水量平衡系统模块,用于计算生成优化调度指令。
1 系统实现方案
系统实现方案如图1所示,通过结合水库的历史来水流量、库内水位、库内水质、应急事件、库内水位等约束条件建立数据融合的模型来生成调度指令,并结合历史调度经验,生成调度信息。
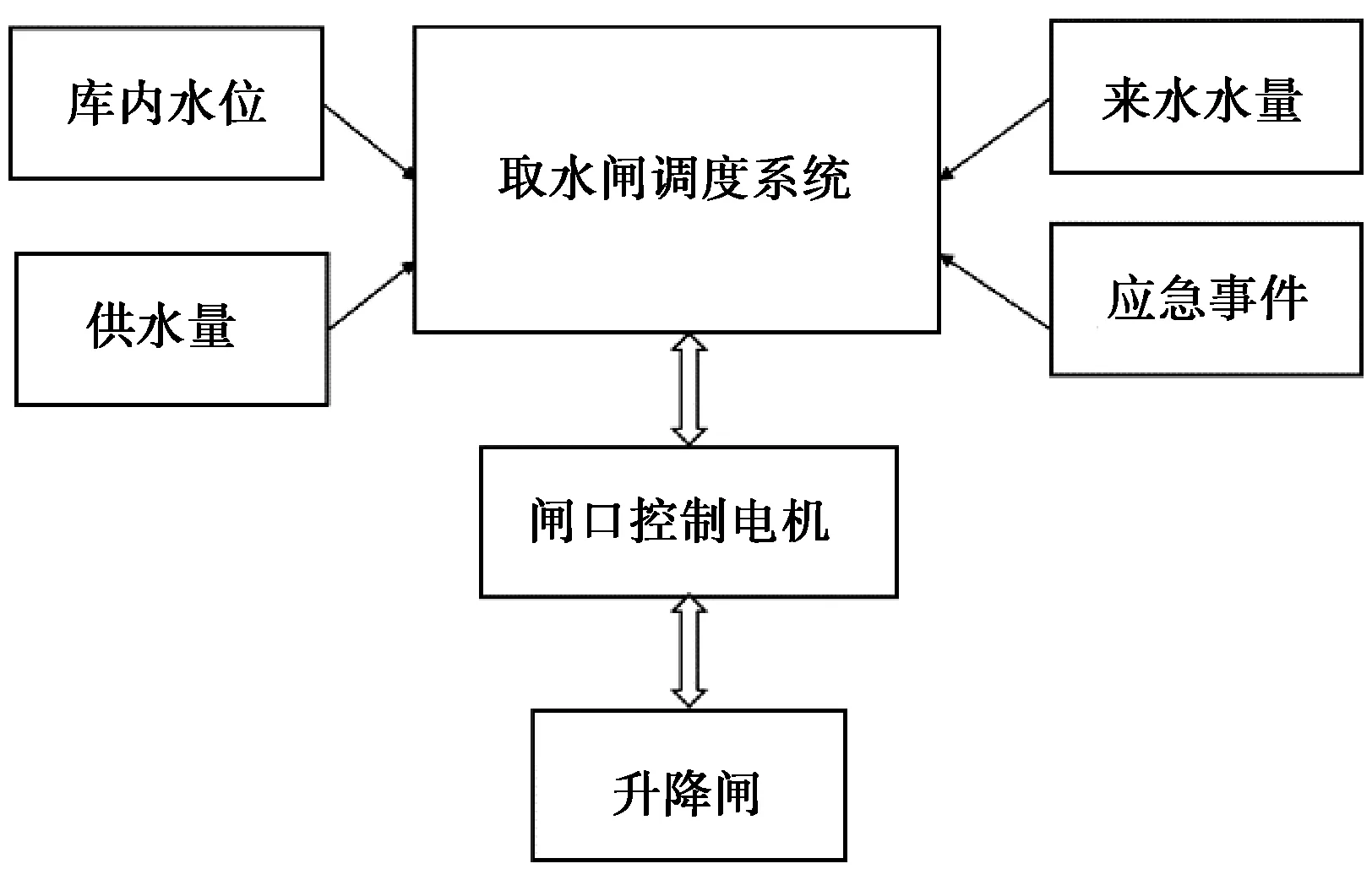
图1 系统实现方案总图Fig.1 Diagram of System Implementation Scheme
本文中数据融合方法的原始数据来自于各传感器的独立观测数据,通过融合产生表示整个系统状态的综合数据,发挥多个传感器的联合优势,提高传感器系统的有效性和鲁棒性,消除单一传感器的局限性[6]。对于本项目,融合水库容量、流量、水位等传感器数据得到当前水库的综合信息,提出了水库水量平衡模型及水量变化公式,分别求出水库库容曲线和闸门水位差流速曲线,用于水量平衡模型关键参数的计算。最后,将水库信息、调度信息、故障信息、约束条件等信息再次融合,通过时间序列分析与回归分析[7-10]等方法得到闸门调度指令。
2 水库水量变化规律
结合数据融合的方法软测量得到水库水量变化方程中的关键变量,闸门流速液位差变化函数曲线与库容变化函数曲线。根据拟合得到的参数与相关数据构建水库水量平衡系统模块,用于计算生成优化调度指令。
2.1 数据来源
所有的数据来源于本文研究水库的数据库系统,以分钟为单位,共调取2017年11月23日—2018年11月22日一年的3个闸门6个开度信息,6个液位计的液位,闸门过水流量,多项故障记录以及多种污染物等信息。为了便于之后的分析,先对各项数据进行预处理。
3个闸门开度分别都有左中右开度,代表闸门开启时相应闸门距离的高度,以其平均值作为闸门开度的代表K1、K2、K3,又由于3个闸门的宽度并不完全相等,以K1d1、K2d2、K3d3作为闸门开启的进水截面积,则闸门进水总截面积S1如式(1)。
S1=K1d1+K2d2+K3d3
(1)
若闸门进水流速为v,闸门进水流量如式(2)。
J=(K1d1+K2d2+K3d3)v
(2)
其中:J——水库取水闸进水流量,m3/s;
K1、K2、K3——3个闸门的开度,m;
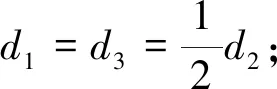
v—取水闸进水流速,m/s。
2.2 水量变化公式拟合
将水库看作一个封闭的简单系统,对水库而言,入库的水只有通过取水闸门流入的部分和来自降雨的部分,出库的水只有通过供水总管流出的部分和自然蒸发的部分,水库里的水量等于水库面积乘以液位高度。因此,它们之间满足基本关系:水量变化=进水量J-出水量G+其他因素(降雨,蒸发等),如式(3)。
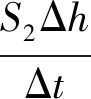
(3)
其中:S2——水库表面积,m3;
Δh——水库液位变化量,m;
G——水库出水流量,m3/s;
other——其他影响因素。
其中,蒸发量与降雨量的作用影响可忽略不计,故公式可简化为式(4)。
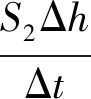
(4)
其中v与S2均为未知量,这里选取1月15日—1月20日的数据进行初步计算,因为有2个未知数,首先排除v的影响,则仅考虑关闸时段的数据。为了排除S2的影响,令Δh为0,则选取同一水库液位的若干数据。经过拟合得到dv、S2,使用得到的参数计算进水量和水库水量,对比出水流量如图2所示。此处的进水流量和出水流量均反应实时的进出水速度,水库水量并不对应左侧y轴的数值,仅反应其水量的多少。
由图2可知,在进水流量大于出水流量时,水库水量增加;而在进水流量小于出水流量时,水库水量减少。同时,在前两日进水流量降为0的小段时间内,水库水量曲线出现了明显的向下波动;而在每天的大约中午时分,进水流量不变,出水量有一个向下的波动。此时,可以看到水库水量向上的趋势有一个明显的减缓,说明研究的水库水量变化规律基本正确。
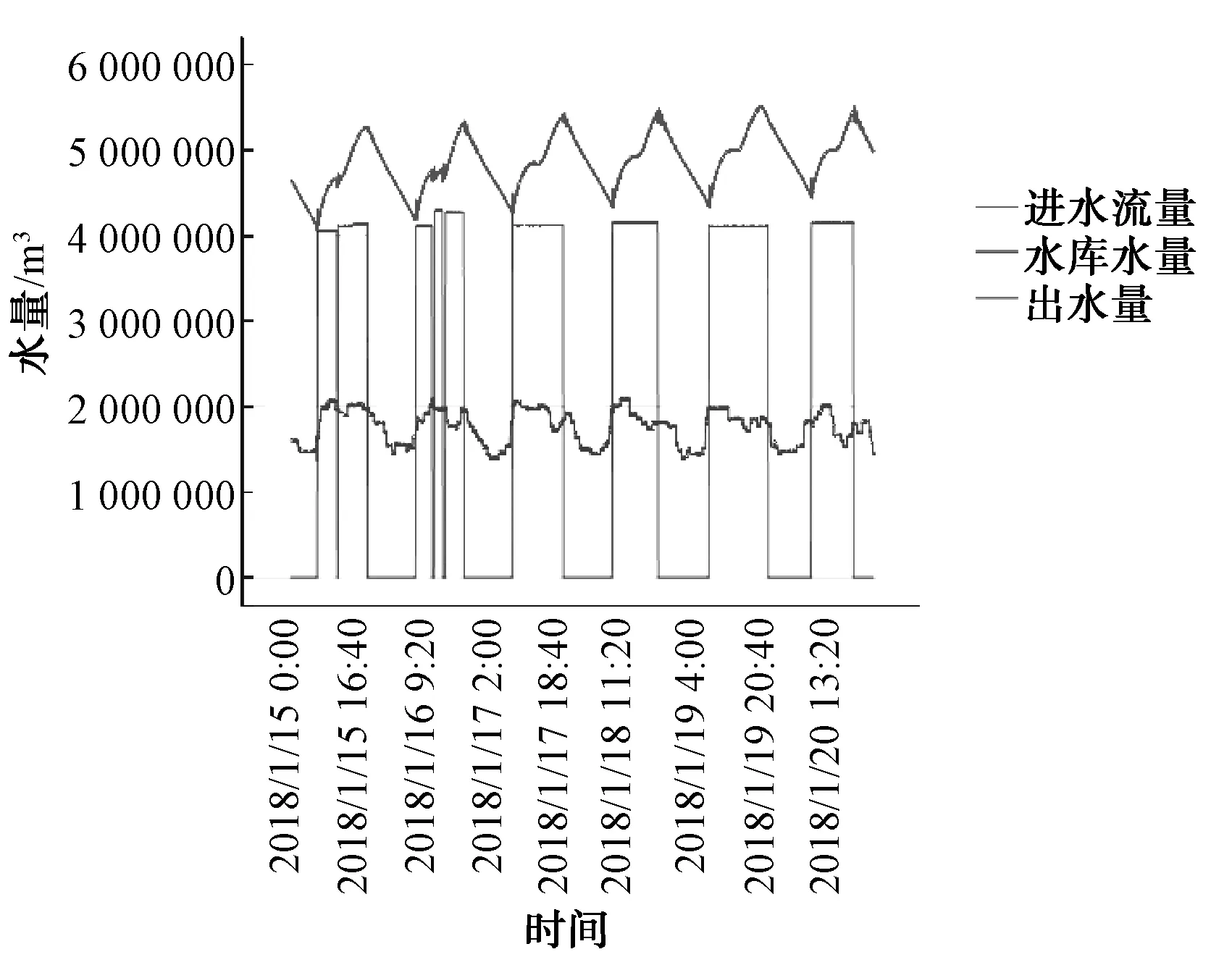
图2 进出水量及水库原水量对比图Fig.2 Comparison of Raw Water Inflow and Outflow and Reservoir Capacity
2.3 不同季节效果分析
不同季节的水量变化存在很大的差异,与流速直接相关的值dv波动越大,对应的效果就越差,由此不应将流速看作一个固定值,而应当对其分别分析研究变化规律。选择季节特征较为明显的月份1月、4月、7月和10月作为研究对象。
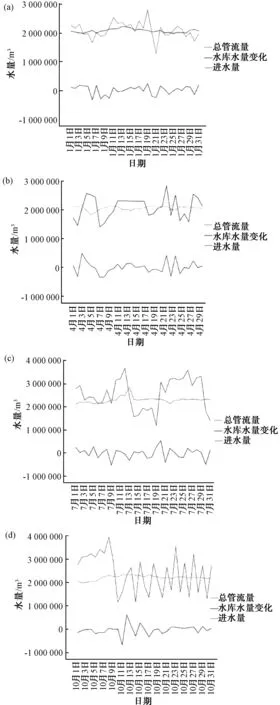
图3 4个月份进出水及原水量变化对比图Fig.3 Comparison of Water Inflow and Outflow and Reservoir Capacity during Four Months
同样,分别对4个月份的数据重新进行参数拟合,由于计算了一个月的数据,此处并不是进出水流速和水量的实时数据,而是代表每一天总体的进水量、出水量以及水库水量的实际变化量。得到的进水量,图3为水库水量变化与出水量对比图。针对4个月的数据重新进行拟合得到的结果,可看出水库进出水量与总管流量直接影响水库水量变化,存在一定的相关性。
2.4 闸门水位差与流速关系
由于闸门水位差会直接影响进水水流速度,故对闸门水位差与流速的相关性进行研究,现对其作斯皮尔曼相关性分析。相关性的强弱由sig值表示,该值越接近于0,则说明相关性越强,一般当sig值小于0.05时,可认为相关性显著。分别对1月、4月、7月、10月的数据进行dv值与闸门水位差的相关性分析,得到的相关系数的符号均为正,故判断dv值与闸门水位差为正相关,如图4所示。

图4 4个月份预测dv值和水位差相关性分析Fig.4 Correlation Analysis of Predicted Water Inflow Velocity and Water level Difference during Four Months
2.5 水库库容曲线
由上一小节得知流速与水位差为正相关,又水库库容与液位值相关,则水库水量变化公式可优化为式(5)。
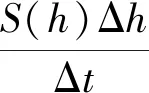
(5)
其中:S(h)——水库库容曲线函数;
v(Δf)——水位差流速关系函数;
Δf——取水闸门内外水位差,m。
S(h)比v(Δf)更好求取,只要取关闸时的数据便可得到一系列连续的数据。而如果先求v(Δf)只能得到一系列间断的点,易出现误差,因此,先求取水库库容曲线。
由于测量仪器的误差以及水面的波动,间隔时间过短会导致很大的误差,则以1 h为间隔,选取全年关闸时段的数据拟合,剔除部分误差数据后,得到水库库容曲线的导数函数如式(6)。
S(h)’=20.259h+155.45
(6)
以水库运营方和监测方给出的水库库容曲线的公共点作为基准值,得到优化后的水库库容曲线拟合如式(7)。
S(h)=10.129h2+155.45h+425.384
(7)
图5为3方水库库容曲线比对图,因为曲线拟合结果取自监测水位数据,故有效水位为1.9~3.12 m。可以看到,拟合得到的水库库容曲线与水库运营方给出的水库库容曲线基本重合,在中间某些值上略低于运营方曲线,而这两者的值均要高于监测方报告中的值,从而验证了拟合得到的水库库容曲线的准确性。
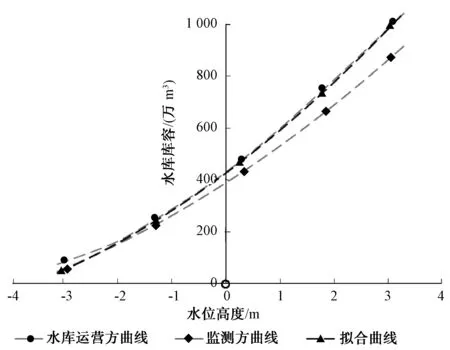
图5 3方水库库容曲线比对Fig.5 Comparison of Three-Way Curves for Reservoir Capacities
2.6 水位差流速曲线
由上一小节已经求得了水库库容曲线,且所有时刻的水位差Δf已知,则水位差流速曲线可由此求得。以1 h为间隔取样,对全年的数据进行回归分析,拟合得到结果如图6所示,将横纵坐标调换后的二次项拟合得到拟合曲线。
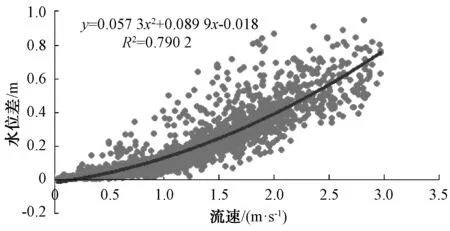
图6 水位差流速曲线拟合Fig.6 Velocity Curves Fitting of Water Level Differences
3 闸门调度方案与程序运行结果
3.1 闸门调度开闸方案
以目前已有的人工闸门调度基本规律为基础,确定闸门自动调控的基本方针,先假定调度要求为8点开闸,开闸液位为2.0 m。如果在8点之前液位降达2.0 m,则提前开闸使8点液位刚好为2.0 m;如果8点的液位仍超过2.0 m,则推迟一定的时间开闸使得达到8点开闸同样的效果。故闸门开闸调度存在两种方案。
(1)开闸方案一
a时刻液位已经到达2.0 m,此时与8点相隔(8-a) h,则为使8点的液位依旧为2.0 m,则从a时刻至8点的进水量和出水量相同,出水量取平均总管流量86 662 m3/h,进水量为86 662(8-a) m3,进水流速v满足式(8)。
Δf=0.057 3υ2+ 0.089 9υ-0.018
(8)
时长较短液位差可近似认为不变,则根据液位差可求得进水流速v,则以进水量86 662(8-a)除以进水截面积S和进水流速v可得需提前开闸的时长b,则(8-b)时刻即为开闸的时间。
(2)开闸方案二
8点的液位超过了2.0 m,为xm,此时若将开闸的时间推迟ah,使得这ah的预测进水量满足式(9)。
J=10.129(x2-4)+155.45(x-2)
(9)
则可近似看作是8点时液位为2.0 m且8点开启闸门。同样,以预测进水量除以进水截面积S以及进水流速v可得到推迟的时间a,则开闸时间为(8+a)时刻。
(3)关闸方案
关闸时间的确定由第2 d开闸的时间差确定,设关闸时间为a,实时水位为bm,则关闸时长为(24+8-a) h,出水量满足式(10)。
G=86 662(32-a)
(10)
a与b满足关系式(11)。
8.666 2(32-a)=10.129(b2-4)+155.45(b-2)
(11)
当a=0时即为关闸时间,若当第2 d为施工作业时,为了保证第2 d 8点的液位低于2.0 m,则取指标如式(12)。
a=10.129(b2-4)+155.45(b-2)
-8.666 2(24+7-a)
(12)
3.2 程序运行结果示意
对2018年11月1日—5日的数据进行分析,取其平均开闸液位和开闸时间作为假想的理想开闸时间和开闸液位,以平均开闸闸门截面积作为理想截面积,剔除检查点某几个过高或过低的之后的液位平均值作为该时刻的理想液位值,以某几个过高或过低液位值偏离理想值的大小作为允许波动范围,其值如表1所示。
程序运行后的结果示意和原调度方案以及液位如图7所示。开度的值为经过近似取整数处理后的值,仅反应近似大小,无具体实际意义。新方案建议中的短时间急剧变化仅代表在此处建议增大或减小闸门开度,不代表实际变化。同时,新方案建议中仅考虑了开闸方案,关闸方案由于原定方案中的关闸后对液位变化产生了干扰,且与开闸方案不同,关闸方案是即时性的,所以不便进行新方案判定,此处不予考虑。
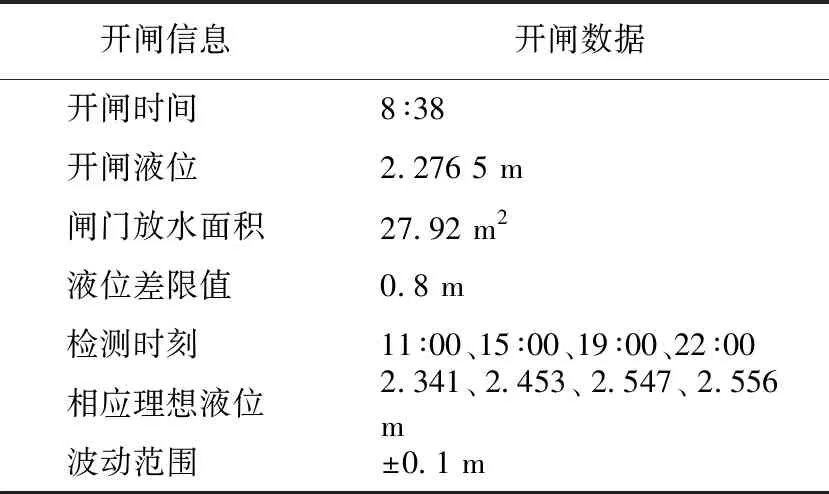
表1 开闸数据分析Tab.1 Data Analysis While Water Intake Gate Opening
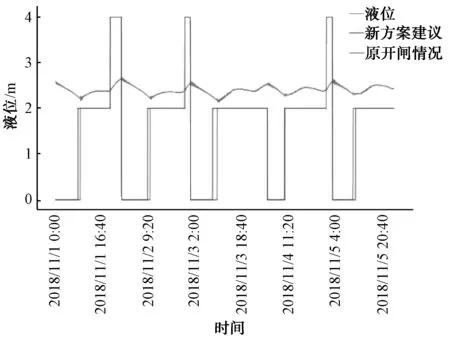
图7 程序运行结果Fig.7 Result of the Program Run
由图7可知,假定的运行结果给出的闸门调度建议和原方案大体相似。由于明确具体的计算在开闸时间上和原开闸方案略有出入,并在检测到水库水量过低或过高时提出了增大或减小闸门开度的建议,势必会使水库的液位变化更加平稳,满足供水要求也不会导致液位过高影响换水周期进而影响水质。
4 总结与展望
取水闸门在线优化系统的完成对于完成整个水库闸门控制系统的半闭环自动化控制奠定了研究基础。本文实现了取水闸门调度相关信息的预处理和分析,由此分析了水库水量的变化规律,给出了水库库容曲线和液位差流速曲线,并由该两条曲线对水库水量的变化规律作出了更精确的描述,结合水库水量变化方程与历史调度规律计算得到优化后的闸门调度指令。该工作的解决方案对于水库闸门的调控有了更精确的把握,进一步挖掘了水库的供水潜能,使得水库液位能够更加平稳、安全,也就使得水库供水能力更加的稳定。对于水库换水周期的把握也能使得水库里水质常年维持在更加良好的状态,这使得整个水库供水地区人们的用水需求得到了一定的保证。同时,也对水库的生态系统起到了一定的保护作用。在闸门调控的方案中,考虑了进水流量过大对水库基底的冲击作用,以及进水量过小导致水位在最低预警液位之下的隐患,这也使得对整个水库以及供水调度起到了一定的缓冲保护作用。同时,因为在晚上对闸门的水位进行了监控,减小了工作人员的压力,也增加了夜晚对突发事件的反应能力,减小了危险事故的发生率。虽然已经基本完成了设计的目标,但是本设计还存在着一些方面的不足。在之后的研究中,可以在调度方案的设计中将污染的因素考虑进去。还对来水河道的液位进行分析综合考量来设计更为合理的调度方案,并考虑对分类为特殊情况的闸门时间序列进行分析找到其共同特征规律,完善相关具体模块以得到完整的可实际运行的相关程序,为水闸的自动化控制系统添砖加瓦。

