我国工业行业技术分解测度与技术溢出渠道分析

尹今格，宗毅君，刘曼琴，孙萌慧

（1.上海立信会计金融学院 国际经贸学院，上海210209；2.上海大学 经济学院，上海200444；3.广东金融学院 经济贸易学院，广州510521；4.山西财经大学 华商学院，太原030032）

一个国家的技术发展程度不仅受国内本行业和其他行业研发投入的影响，而且通过各种渠道受国外技术发展程度的影响，这就使得度量行业内研发及不同渠道溢出对行业技术发展的影响程度有必要。潘文卿等［1］利用我国投入产出表的数据衡量了产业间技术溢出，发现产业间技术溢出对我国工业各部门劳动生产率有着显著的正面影响。黄漓江和桑百川［2］利用我国制造业企业微观数据检验进口溢出，发现尽管进口溢出对企业生产率的影响显著为正，但当技术差距较大时进口溢出反而抑制了企业生产率。朱福林等［3］考察了我国服务贸易进口渠道的R&D 溢出，发现国内R&D 投入及国际R&D 溢出与全要素生产率具有较稳固的协整均衡关系。陈启斐和刘志彪［4］利用47 个国家的双边服务贸易考察了进口服务贸易所产生的技术溢出。尽管现有文献考察了国内外各种技术溢出渠道，但将这些渠道放在一个框架之内且利用我国工业行业数据进行分析的还很鲜见，为此，本文将国内外多种渠道的技术溢出放在同一框架内进行分析。

Fare 等［5］提出的基于数据包络分析法（date envelope analysis，DEA）的Malquist 指数法是目前度量技术的广泛使用的方法之一，该方法的优点在于不需要对生产函数的形式进行具体设定。Malquist 指数由效率指数和技术进步指数相乘得到，效率指数反映了和上一期相比，该生产单位距离生产最佳前沿面的变化程度，技术进步指数反映了和上一期相比，生产最佳前沿面本身的变化程度。吕忠伟和李峻浩［6］使用该方法对我国国内区域间的技术溢出进行了研究。李小平和朱钟棣［7］使用该方法对我国工业行业1999—2003 年的国内及进口溢出进行了研究。本文将以1991—2010 年我国工业行业为研究对象考察国内本行业研发资本变动、国内其他行业研发溢出、进口贸易渠道的研发溢出和出口贸易渠道的研发溢出对技术效率的提高、技术进步和全要素生产率变动的贡献。本文使用20 年的时间段，且不仅考虑了进口渠道的溢出而且考虑了出口渠道的溢出，使得结果更全面，更客观。

一、理论及计量模型的建立

首先，设定以下柯布-道格拉斯生产函数：

其中：i 表示行业；t 表示时间；Y 表示产出；A 表示技术水平或全要素生产率（TFP）；L 表示生产过程中的劳动投入；K 表示生产过程中的资本投入。按照以Romer 和Paul［8］、Lucas 和Robert［9］等为代表的内生增长理论，技术是由追求利润最大化的厂商进行研发投资的结果；按照Romer 和Paul［10］及Grossman 和Helpman［11］等的研究，一国的技术不仅受其本身研发投入的影响，而且通过各种渠道受到其他国家研发投入的影响，即产生技术溢出。即使在一个国家内部行业之间的研发投入也会产生技术溢出，即一个行业的技术水平不仅会受到本行业的研发投入的影响，而且受到其他行业的研发投入的影响，即行业之间的技术溢出。按照以上分析，对全要素生产率作出以下规定：

其中：g 表示不受任何因素影响的技术的自然增长率；β 表示弹性，即解释变量变动1 个百分点时，会引起被解释变量变动几个百分点；RDit表示i 行业本身的研发资本存量；IMit表示i 行业通过进口获得的研发溢出；EXit表示i 行业通过出口获得的研发溢出；ORDit表示i 行业从其他行业获得的研发溢出。对式（2）两边进行全微分并将两边同除以TFPit可得：

式（3）衡量了影响全要素生产率的各种因素的增长率对全要素生产率的增长率的影响。在式（3）的基础上加入随机扰动项即可得到本文使用的计量模型：

实际上，全要素生产率的增长率可以进一步被分解为技术效率（EFF）的增长率和技术进步（TECH）的增长率，前者衡量了在既定的技术水平下，生产效率的改进程度，后者衡量了技术进步程度。假设影响技术效率增长率和技术进步增长率的因素相同，可以建立以下两个计量模型：

二、指标构建及数据来源

（一）指标构建

本文利用式（4）～式（6）所表示的计量模型考察国内本行业研发、国内其他行业研发、与14 个发达经济体①14 个发达经济体分别是美国、日本、英国、法国、德国、澳大利亚、加拿大、意大利、比利时、丹麦、芬兰、爱尔兰、荷兰、西班牙。的进口和出口贸易对我国全要素生产率、技术效率提高和技术进步的作用。用到的被解释变量指标有全要素生产率增长率、技术效率增长率、技术进步增长率。解释变量指标有国内本行业研发资本增长率、国内其他行业研发资本增长率、通过进口获得的研发资本增长率和通过出口获得的研发资本增长率4 个变量。被解释变量指标的构建在下一部分给出。本节主要说明4 个解释变量指标的构建。

假定一个行业的技术不仅受国内本行业研发投入的影响，而且通过投入产出等渠道受国内其他行业研发投入的影响，则国内其他行业研发资本存量数据由该行业之外的其他行业的研发资本存量简单加总得到。

Grossman 和Helpman［12］（以下简称CH［12］）首次构建了通过进口贸易渠道的研发资本存量指标，用表示，构建方法如下：

其中：mijt为i 行业t 年从j 国的进口量；mit为i 行业t 年从这14 个国家的进口总量为j 国t 年的国内研发资本存量，该指标受到众多学者 的研究 与评价（Lichtenberg 和Potterie［13］，Keller［14］，Funk［15］），其中Lichtenberg 和Potterie［13］（以下简称LP［13］）指出该指标存在潜在的加总偏误，即假设一个国家的贸易伙伴国合并时，其国外R&D 资本存量会大量增加，即使与贸易伙伴国的贸易流量及贸易伙伴国国内的R&D 存量都没有发生变动。在此基础上LP［13］构建了如下进口渠道的研发资本存量指标，用表示：

其中：yjt为j 国t 年的研发资本存量。该构建方法修正了CH［12］潜在的加总偏误。

Funk［15］则通过与CH［12］类似的方法构建了通过出口贸易获得的国外研发溢出，用表示，构建方法如下：

其中：exijt为i 行业t 年从j 国的出口量；exit为i 行业t 年从这14 个国家的出口总量。类似于LP［13］的观点，本文认为该方法同样存在潜在的加总偏误，即如果两个贸易伙伴国合并会导致通过出口获得的国外研发资本存量的增加，即使贸易总量、结构与贸易伙伴国的研发资本存量都没变，类似于LP［13］，本文提出如下方法修正潜在的加总偏误：

本文计量模型用到的是各指标的增长率，所以需要对以上构建的各指标取时间差分并除以上一年度的值得到其增长率。

（二）数据来源

本文用到的数据有1990—2010 年各个行业的GDP、工业分行业职工人数、固定资产投资数据、分行业国内研发内部支出数据、分别从14 个主要经济合作与发展组织（Organization for Economic Co-operation and Development，OECD）国家的行业进出口数据、各行业总的进出口数据、上述14 个国家的GDP 与研发投入数据。GDP 数据和固定资产投资数据来源于《中国统计年鉴》（2002—2011），工业分行业资本存量和从业人数的数据均直接使用陈诗一［16］附表2 和附表3 所提供的数据并使用《中国统计年鉴》（2010—2011）将其扩充到2010年，国内研发投入的数据来自《中国科技统计年鉴》（2002—2011），进出口数据来源于联合国COMTRADE 数据库并借鉴盛斌［17］将数据转换到《国民经济行业分类》（GB/T 4754—2002）二位码的数据，由于能够获得的数据有限，OECD 国家的GDP 数据与研发投入数据均为国家总值，数据来源是国研网OECD 数据库。

三、计量分析及结果

（一）全要素生产率的计算

关于全要素生产率的计算方法有多种，对各种方法的介绍及分类参见文献［18］。本文使用Fare 等［5］所使用的非参数方法中的Malquist 指数法。该方法的特点如下：不需要设定具体的函数形式，允许经济单位不处于最佳效率状态，可以用于多投入多产出的情况，不需要投入及产出的价值数据。其基本思想如下：先确定每期所有生产单位（本文是行业）中处于效率最佳的生产单位即最佳前沿面，然后将其他生产单位同最佳前沿面相比，通过比较当期和上一期距离最佳前沿面的距离变化得出效率指数，反映了技术追赶程度，将和上一期相比在各生产单位投入条件下最佳前沿面的相对移动得出技术进步指数，反映了技术变革或创新程度，最后将二者相乘得到全要素生产率指数。技术效率的计算方法有两种，一种是基于投入的技术效率，即在产出确定的情况下，最小投入与实际投入之比；另一种是基于产出的技术效率，即在投入一定的情况下，实际产出与最大产出之比。这里以基于产出的技术效率为例，规定如下距离函数：

该函数表示，在投入一定的情况下，将生产移动到最佳前沿面时，其产出将扩张倍。注 意 到，因此，当生产处于最佳前沿面时。效率指数测度了和上一期相比距离最佳前沿面的变化程度，其表达式为

技术进步指数测度了和上一期相比，最佳前沿面的移动程度，其表达式为

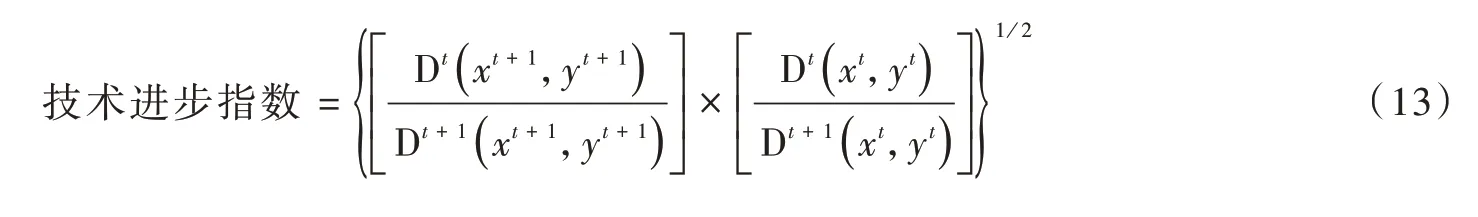
全要素生产率即Malquist 指数是效率指数和技术进步指数的乘积，即

假设t 时期i = 1，…，I 个生产单位使用n = 1，…，N 种投入xi，tn生产m = 1，…，M 种产出yi，tm。最佳前沿面的技术是基于以下方式确定：

该计算需要满足的前提条件是具有不变规模报酬和生产要素强可处置（详细参见文献［5］）。

以上求出的效率指数、技术进步指数与全要素生产率指数均为本期与上一期的比值，要想得到增长率指标，需要将各指数减1。

（二）计量分析结果

首先需要对各变量进行平稳性检验以避免伪回归的出现。这里使用第一代面板单位根检验中的LLC（Levin 等［19］、Breitung［20］、Hadri［21］、Maddala 和Wu［22］的Fisher-ADF）4 种检验方法，前两种属于同质单位根检验，后两种属于异质单位根检验，第三种的原假设为平稳，其余原假设为存在单位根，检验结果见表1。各个指标中为 行 业 内 研 发 资 本 存 量 的 增长率为 按 照CH［12］构 建 的通过进口获得的国外研发资本存量的增长率

为 按 照LP［13］构 建 的 通 过 进 口 获 得 的 研 发资 本 存 量 的 增 长 率为 借 鉴CH［12］构建的通过出口获得的国外研发资本存量的增长率，为 借 鉴LP［13］构 建 的 通 过 出 口 获 得的国外研发资本存量的增长率为生产效率的增长率为 技术进步的增长率为全要素生 产率增长率。由于所有的变量都是经过差分处理的，所以所有的变量均显示平稳。为 其 他 行 业 研 发 资 本 存量的增长率

表1 面板单位根检验结果

其次，由于本文有4 个解释变量，所以需考虑多重共线性问题。尽管变量取差分可以减轻多重共线性问题，但经过检验，发现变量gordit与grdit及gexCHit存在较强的线性关系，在此，借鉴Kokko［23］做出如下处理：将gordit对grdit及gexCHit做出回归，也将gordit对grdit做出回归：

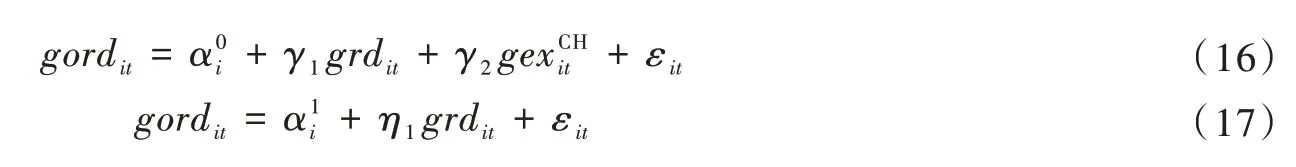
接下来进行计量分析。为了进行稳定性检验，同时观察是否还存在多重共线性问题，本文在回归时将解释变量逐次纳入。被解释变量有三个：gtfpit、geffit、，本文首先将geffit对解释变量做回归，其次将gtechit对解释变量做回归，最后将gtfpit对解释变量做回归。回归方法采用的是面板固定效应模型，geffit对解释变量的回归结果见表2。

从表2 可以看出，首先，每个变量在以上各模型中结果非常一致，所以可以推断，多重共线性已经得到消除。从结果来看，国内本行业的研发和国内其他行业的研发均对技术效率的提高产生了负的效应，且国内其他行业研发资本变动产生的负效应更大一些，应该是由于研发活动会挤占一定的资源。借鉴CH［12］所构造的进口贸易渠道的溢出和出口贸易渠道的溢出均为正，但值都很小而且均不显著，借鉴LP［13］所构造的进口贸易渠道的溢出为正，出口贸易渠道的溢出为负，绝对值都很小，且均不显著。所以，总体来看，国内行业内与行业间研发资本的变动对技术效率的提高产生了负向的作用，而进出口渠道的技术溢出对技术效率的提高没有产生显著的作用。

表3 为技术进步指数对各解释变量的回归结果。就该组回归结果来看，行业内和行业间研发资本的变动都对技术进步产生了显著的正效应，且行业间研发溢出的效应更大一些，几乎是行业内研发效应的两倍。借鉴CH［12］所度量的进口贸易的溢出效应和出口贸易的溢出效应均为正且较小，但进口溢出显著，而出口溢出不显著。借鉴LP［13］所度量的进口溢出和出口溢出也均为正且值较小，但两种渠道的溢出均显著。总体来看，国内研发支出和通过进出口贸易获得的研发溢出均对技术进步产生了正向的效应，且国内效应要远大于通过进出口获得的溢出效应。

表2 固定效应面板估计结果（被解释变量geffit）

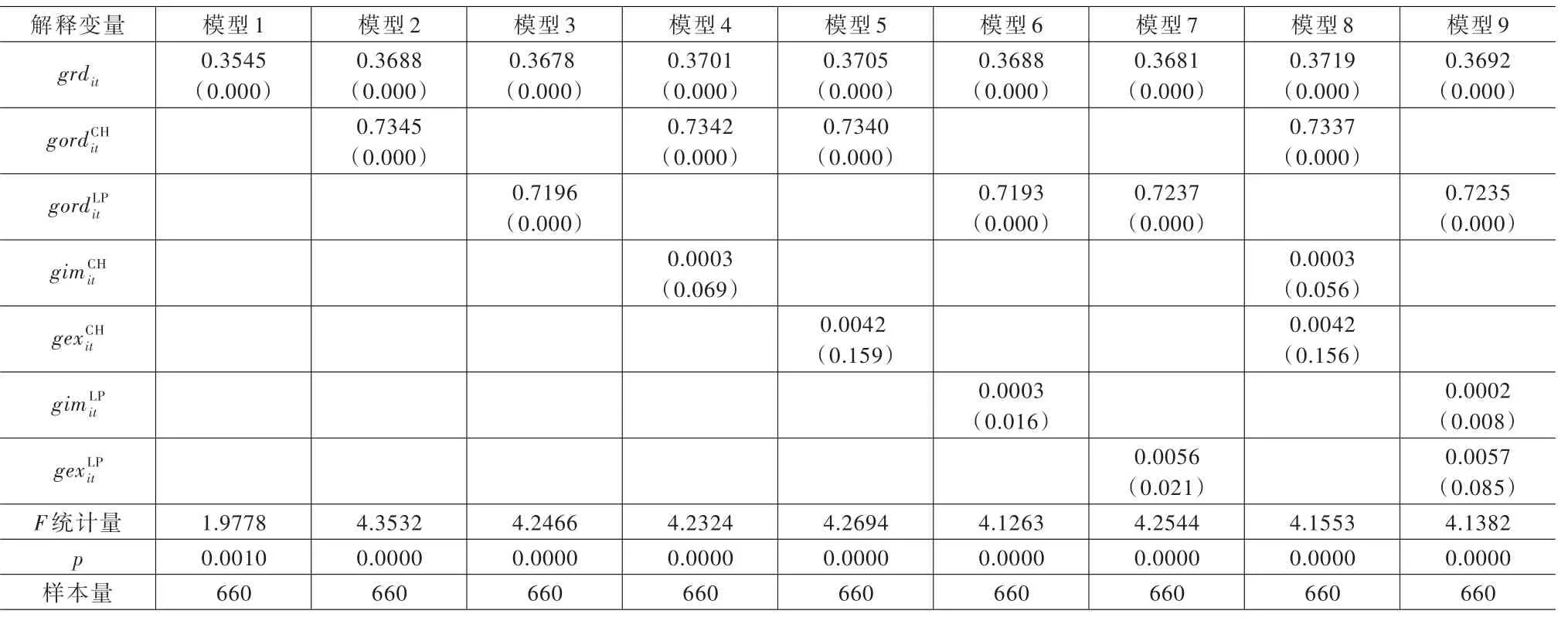
表3 固定效应面板估计结果（被解释变量gtechit）

表4 为全要素生产率即Malquist 指数对各变量的回归结果。就该组回归结果来看，国内本行业研发资本存量的变动对全要素生产率的变动产生的效应为正且显著，而国内行业间研发溢出对全要素生产率提高产生负的效应但不显著，可能是由于对技术效率提高产生的负向效应和对技术进步产生的正向效应相互抵消所致。借鉴CH［12］度量的进出口溢出均显著为正，且出口溢出的绝对值要大一些。借鉴LP［13］度量的进口溢出显著为正，出口溢出也为正但不显著，应该是由于出口对技术效率提高作用的不显著占了主导地位。不管进出口溢出显著与否，和国内研发效应相比，其绝对值均要小，所以我国还是应该加大国内研发投入。另外，考虑到借鉴CH［12］所构建的出口渠道的研发溢出对技术效率的提高和对技术进步产生的效应均不显著，而对全要素生产率的提高产生的效应为正且显著，这种不一致可能是由于LP［13］指出的该指标本身的内在缺陷所致，因此，本文认为借鉴LP［13］所构建的国外研发资本更能够客观的反映我国通过国际贸易渠道所获得的溢出效应。

表4 固定效应面板估计（被解释变量gtfpit）

四、研究结论

本文分别度量了国内本行业研发效应、国内其他行业研发效应、进口贸易渠道的研发溢出和出口贸易渠道的研发溢出4 种效应对生产效率的提高、技术进步和全要素生产率的提高所产生的作用，使用Fare 等［5］所介绍的方法计算技术效率指数、技术进步指数以及由二者相乘所形成的Malquist 指数即全要素生产率指数。其他行业的研发支出由该行业之外的其他行业的研发支出加总形成，通过进出口贸易渠道获得的国外研发资本分别借鉴CH［12］和LP［13］两种方法分别进行构建。结果表明，国内本行业的研发和国内其他行业的研发对生产效率的提高均产生了负向的效应，应该是由于研发要占用一定的资源所致，进出口渠道的研发溢出对生产效率的提高没有产生显著的作用。国内本行业的研发支出和国内行业间研发溢出对技术进步均产生了显著的正向作用，且国内行业间研发溢出的效应更大一些。国际贸易渠道的技术溢出对技术进步也产生了正向的溢出但比国内研发的效应要小，且出口溢出产生的效应更大一些。就对全要素生产率的贡献来看，行业内研发支出的效应为正，行业间研发溢出效应不显著，可能是由于对效率提高的负向效应和对技术进步的正向效应相抵消所致。进口溢出对全要素生产率的贡献为正，而出口溢出对全要素生产率的贡献不显著。就回归结果判断，借鉴LP［13］所构建的国际贸易溢出指标和借鉴CH［12］所构建的溢出指标相差不大，但前者要稍由于后者。总体来看，我国应该进一步加大国内研发投入，而对于进出口贸易则一方面要对国外技术进行更充分的吸收利用，另一方面，要利用出口时机，提高的技术含量，以带动国内技术进一步提升。