一种基于EPR对纠缠相干性的量子签名协议
张 玮,陈永志
(石家庄学院 机电学院,河北 石家庄 050035)
0 引言
数字签名也称电子签名,是对现实生活中手写签名的数字模拟,是信息安全的核心技术之一,也是安全电子商务和安全电子政务所依赖的关键技术之一.根据签名的鉴定方式不同,数字签名协议可以分成两种方式,分别是直接式的签名鉴定方法和间接式的签名鉴定方法.直接式的鉴定方法是由收到方进行执行,简称为真实数字签名;间接式的鉴定方法是由第三方去执行,第三方充当仲裁者的角色,因此此种签名也被称为仲裁数字签名.
量子保密通信虽然与经典密码学一样需要涉及到信息签名问题,但是随着计算机技术的发展和计算能力的提高以及量子计算机的出现,基于数学难解性问题的经典签名方案极容易被攻破,而量子签名由于是基于量子物理特性从而具有无条件安全性.因此,量子签名引起了人们的研究兴趣.
曾贵华等[1]的基于GHZ三重态粒子的量子信息签名方案是较早提出的量子签名方案,但该方案属于仲裁签名方案,需要第三方一个可信赖的系统管理员的参与.第三方的存在会降低系统效率,同时也会增加不安全因素.随后,人们又研究提出了一些无需第三方存在的各类真实量子签名方案[2-12],这些方案或基于测量结果比较,或基于量子秘密共享,或基于量子隐形传态.本研究仅利用EPR粒子对的纠缠特性和量子密钥分发(QKD)技术,提出了一个无需第三方存在的、比上述方案更加简洁的量子签名方案.
1 基本原理
本研究所使用的量子测量将用到的两种彼此非正交的测量基:基BZ和基BX.其中{∣0〉,∣1〉}是一组标准正交基,{∣+〉,∣-〉}称为基BZ;构成另一组正交基,称为基BX.基BZ和基BX之间的关系为:
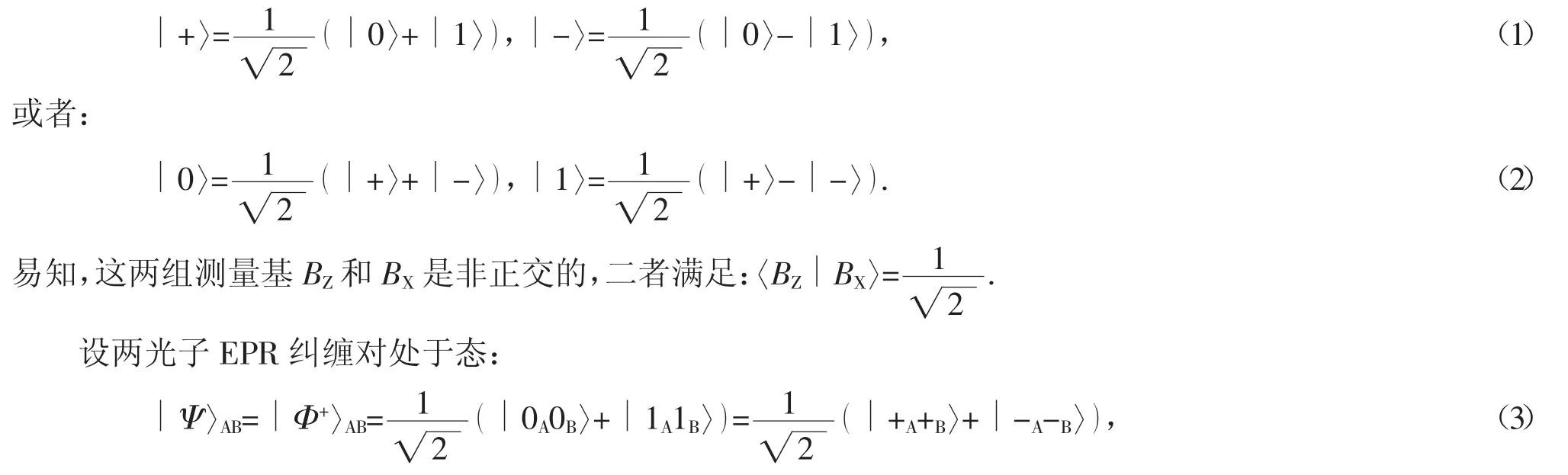
设Alice拥有其中的光子A,Bob拥有光子B.由(3)式可知,不论两个光子相距多远,由于EPR对的纠缠特性,当Alice这边测量光子A后,Bob那边光子B必然会坍缩到与光子A相同的状态.因此,若Alice和Bob在基BZ和BX中选用相同的基来分别测量他们的光子,必然得到相同的结果.然而,Alice若选用某一基测量后,Bob采用与之不同的另一基进行测量,由(1)式、(2)式可知,其将得到一个随机的结果.
2 协议设计
设签名人为Alice,验证签名人为Bob.Alice要发送的真实消息为:

M是一组N位二进制序列.
2.1 协议初始化
1)Alice制备N组(3)式所示的EPR纠缠对粒子,自己留下粒子A,将粒子B按顺序分发给Bob.
2)密钥分发:Alice与Bob共享密钥KAB(2N-bit),KAB的分发可以通过著名的BB84或B92 QKD协议.设 KAB={k(1),k(2),…,k(2N)}.
2.2 签名过程
1)Alice 根据真实消息 M 的每位 m(i)二进制值来选用测量基 Bz={∣0〉,∣1〉}或 Bx={∣+〉,∣-〉}对其手上的粒子A序列进行测量.测量规则如下:

Alice将测量结果按下式编码为2-bit经典信息:

2)Alice将上面编好的经典信息W={w(i)}按每2-bit一组用她与Bob的共享密钥KA(B2N-bit)加密,记为.
3)Alice将S作为对消息M={m(i)}的签名发送给Bob.
2.3 验签过程
1)Bob收到Alice的签名S后,用共享密钥KAB解密,得到经典信息W={w(i)}.
2)Bob按2-bit一组的经典信息w(i)={00,01,10,11}按下面的测量规则测量自己手上的粒子B序列:

3)Bob 上面的测量结果为量子态{∣0〉,∣1〉,∣+〉,∣-〉}之一,将其按(6)式编码为 2-bit经典信息,记为w′(i).Bob对自己手上的粒子B序列依次测量,得到经典信息W′={w′(i)}.
4)Bob将得到的W′={w′(i)}与收到的W={w(i)}进行对比,若有w′(i)=w(i)或W′=W,则签名验证通过.否则,拒绝签名.
3 协议特性分析
3.1 方案的正确性
由(3)式可知,若Alice和Bob双方均采用同一测量基Bz或Bx测量,测量塌缩后A与B两粒子的量子态总量相同,因此由(4)、(5)、(6)式可知,总会有W′=W.而双方若都遵循协议步骤进行签名和验证,签名总是会验证通过的.
3.2 方案的无条件安全性
1)本协议QKD采用成熟的BB84协议或B92协议,这些QKD协议都已经被证明具有无条件安全性.
2)量子信道的安全性,可采用双方交替使用同一测量基Bz或Bx测量EPR纠缠对的方法检测量子信道∣Φ+〉AB,如果有攻击将会在检测中发现.
3)假设攻击者Eve截获了签名S及消息M,她想篡改M同时篡改S而不被发现.由于对∣Φ+〉AB态测量塌缩是随机的,经典信息W={w(i)}靠杜撰肯定不能和Bob手上粒子序列B塌缩后的状态相符,攻击将会被发现,Eve的阴谋不会得逞.
4 结论
所提出的量子签名协议仅利用EPR粒子对的纠缠特性和QKD技术,通过非正交基测量实现了签名及其验证,无需第三方存在,更加简洁可靠.由于协议基于量子力学的物理特性,因此具有无条件安全性.

