基于SVM的新能源公交车运营里程核查方法

张文华，张志俊

(长安大学经济与管理学院，陕西 西安 710061)

0 引 言

近年来，在坚持绿色发展理念的导向下，国家政策大力支持新能源公交车的推广和应用，新能源公交车的数量与日俱增，同时，国家也出台了一系列的新能源汽车补贴政策，为了保证补贴申报工作的顺利进行，应该重视新能源公交车的申报数据核查。新能源公交车审核主要是通过资料审核和实地核查相结合来确保申报数据的真实性。资料审核主要是审核网上的新能源公交车运营里程申报数据，而核查网上申报数据工作量大，没有专门的方法，核查效率低。如何利用专门的异常值检测算法更加高效地审核新能源公交车的运营里程申报数据，找出可疑的车辆，为实地核查提供参考依据，是亟待解决的问题。

目前，没有检索到有关新能源公交车运营里程申报数据核查方法的研究。在统计学领域，数据异常点检测方法是比较多的，最常用的异常值检测算法大致可分为基于距离的异常点检测算法和基于密度的异常点检测算法。

1)基于距离的异常点检测算法。文献[1-2]提出了IForest方法用于检测异常值，文章表明，该方法能够有效检测异常值。该方法更适合处理连续的数据集，对于全局稀疏点比较敏感，不擅长处理局部的相对稀疏点，当某些局部的异常点较多时，算法检测的准确率会下降。文献[3-17]是基于SVM算法检测异常值，比如财务数据、网络数据和养殖数据等。文章表明，支持向量机能够有效地检测出异常值，支持向量机的准确率要高于传统的方法(比如朴素贝叶斯等)。SVM算法可利用核函数将低维空间的数据映射到高维空间中，使分类问题变得简单，其中线性核函数具有参数少、速度快等优点。

2)基于密度的异常点检测算法。文献[18-24]提出了改进的局部离群点检测算法，改进的LOF算法能够更高效地检测出异常值，但是在使用该算法时，数据集需要满足一个条件：不存在大于等于K个重复的点，因为当这样的重复点存在的时候，这些点的平均可达距离零，局部可达密度就变为无穷大，会给计算带来一些麻烦。文献[25]提出将支持向量机和K-means++算法结合的入侵检测模型，将2种异常值检测算法相结合，能够提高检测率和检测速度。

综上所述，专门的异常值检测算法主要有IForest算法、LOF算法和SVM算法等，每种算法都有其各自的特点及适用范围。本文针对H省新能源公交车运营里程申报数据的核查问题，结合要处理数据的特点，选择线性SVM算法，利用该算法检测出新能源公交车运营里程申报数据中的可疑数据，为新能源公交车实地核查提供参考依据。

1 支持向量机(SVM)

1.1 算法介绍

SVM(Support Vector Machine)是一种常见的判别方法，分为线性SVM和非线性SVM这2大类，本文只讨论线性SVM。在机器学习领域，SVM算法是一种有监督的学习方法，能够利用预测值与实际输出值产生的误差，进行误差反向传播修改权值来完成网络修正，使得预测效果更加贴合实际。

线性SVM的主要思想：对于多维数据集，系统随机产生一个超平面，对样本进行分类，直到训练样本中属于不同类别的样本点正好位于该超平面的两侧，满足该条件的超平面两侧的空白区域最大化，从而实现对线性可分样本的最优分类，该算法几何解释如图1所示。

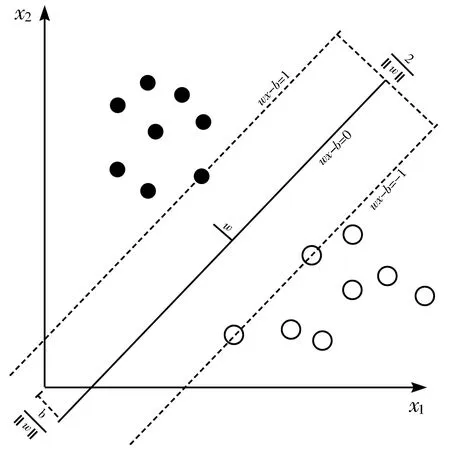
图1 线性SVM算法样例

由图1可知，图中实线就是最大间隔分离超平面，该平面将二维空间中的数据分为2类。虚线上的点为支持向量，SVM算法由少数支持向量决定了最终结果。

1.2 SVM算法原理

SVM算法属于二分类算法，可分为线性SVM算法和非线性SVM算法。本文根据要处理数据的特点，选择线性SVM算法，算法求解过程如下：

1)输入线性可分数据集T={(x1,y1),(x2,y2),…,(xn,yn)}，其中xi∈Rm,yi∈{1,-1},i=1,2,…,n(n为训练样本数)。

2)建立目标方程：

(1)

s.t.yi(wT·xi+b)-1≥0,i=1,2,…,n

将式(1)中的约束条件融合到目标函数中，建立拉格朗日公式，结果如式(2)：

(2)

s.t.αi>0

优化目标，得式(3)：

(3)

求式(3)的对偶问题，得式(4)：

(4)

对w、b求极小值，即对w和b求偏导，并令其值为0，得式(5)和式(6)：

(5)

(6)

将w和b代入式(2)，得式(7)：

(7)

s.t.αi≥0,i=1,2,…,n

由式(7)求出α，则可求出w*和b*，如式(8)和式(9)：

(8)

(9)

3)输出最大间隔分离超平面，如式(10)：

w*·x+b=0

(10)

线性可分支持向量机为：

f(x)=sign(w*·x+b*)

1.3 算法评价

异常值检测算法最常用的评价指标有准确率、特效度(检出率)和检错率，通常来说，准确率和特效度越高、检错率越低，算法越好。该算法准确率、特效度和检错率的数学表达式如下：

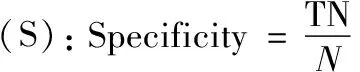
其中，TP表示将正类预测为正类，TN表示将负类预测为负类，FP表示将正类预测为负类，P表示正类，N表示负类。

2 实证分析

本文以H省新能源公交车年运营里程申报数据核查为研究对象，利用线性SVM算法检测运营里程申报数据中的异常值，研究过程如图2所示。

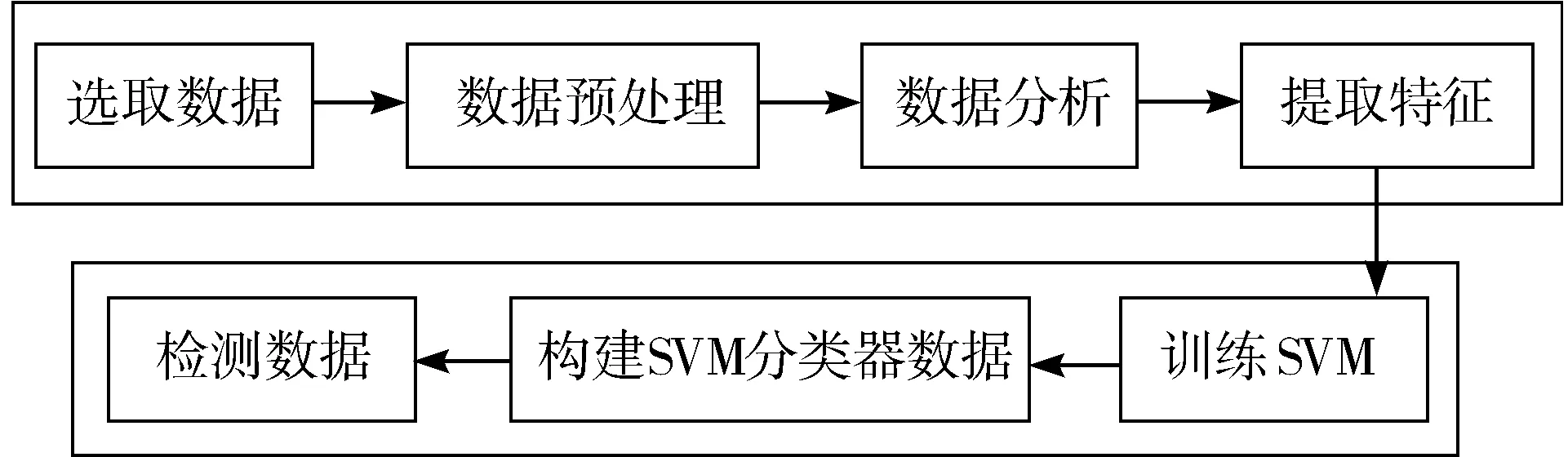
图2 基于SVM算法的运营里程申报数据核查过程

2.1 数据选取及处理

选取H省2017年《节能与新能源公交车运营明细表》中的新能源公交车数据，数据样例如表1所示。

表1 《节能与新能源公交车运营明细表》的数据样例

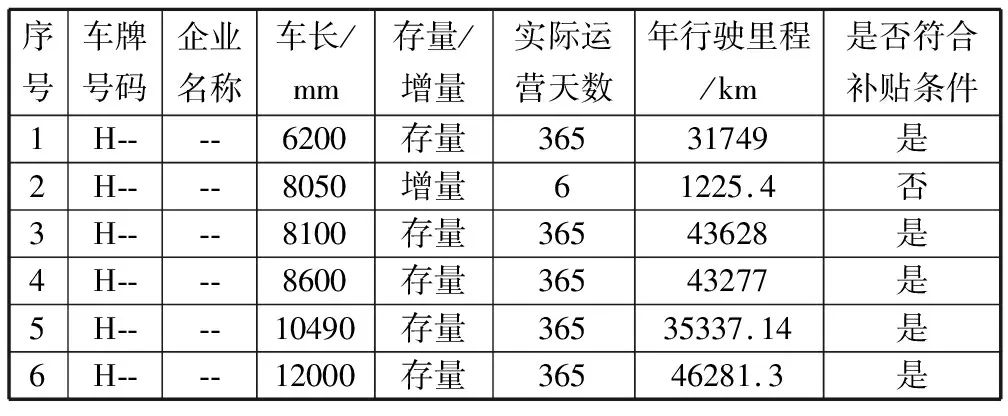
序号车牌号码企业名称车长/mm存量/增量实际运营天数年行驶里程/km是否符合补贴条件1H----6200存量36531749是2H----8050增量61225.4否3H----8100存量36543628是4H----8600存量36543277是5H----10490存量36535337.14是6H----12000存量36546281.3是

表1中有7个重要的属性，分别为车牌号码、企业名称、车长、存量/增量、实际运营天数、年行驶里程和是否符合补贴条件。在实际的新能源公交车运营里程核查工作中，主要看表中车辆是否符合补贴条件及其年运营里程这2项数据。为了方便后续数据分析，需要对原始数据进行预处理，筛选出系统显示符合补贴条件的车辆，由于符合补贴条件的车辆基本上是存量车辆，仅有少量增量车辆，故在做数据分析时只考虑存量新能源公交车，经过数据预处理，筛选出3427辆符合补贴条件的存量车辆。

2.2 数据分析

2.2.1 描述性分析

为了了解新能源公交车运营里程申报数据的整体分布情况，选择新能源公交车车辆长度和年运营里程做数据分析，分析结果如图3所示，横坐标表示车辆长度(m)，纵坐标表示年运营里程(104km)。

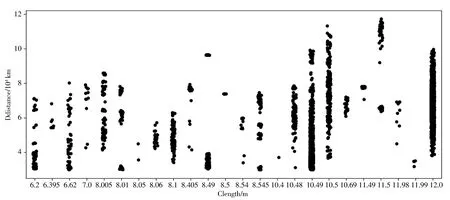
图3 不同车长运营里程数据的散点图

由图3可知，从全局来看，车辆年运营里程达到105km以上的车辆数相对较少。新能源公交车年运营里程与其车长有一定的关系，从数据分布特征来看，运营里程的Kurtosis=-0.43053<0, Skewness=0.356669>0，得出该数据分布比较倾斜，属于非高斯分布。考虑到数据分布的特征，SVM算法是非常适合处理该数据集的，在选择数据处理模型时，选择线性SVM模型。

考虑到车辆年运营里程与地域(公交线路)有关，故根据车辆所在的运营区域，将地域分为城镇、省会市区和其他市区，分析新能源公交车的车辆类型与地域的关系，分析结果如图4所示。

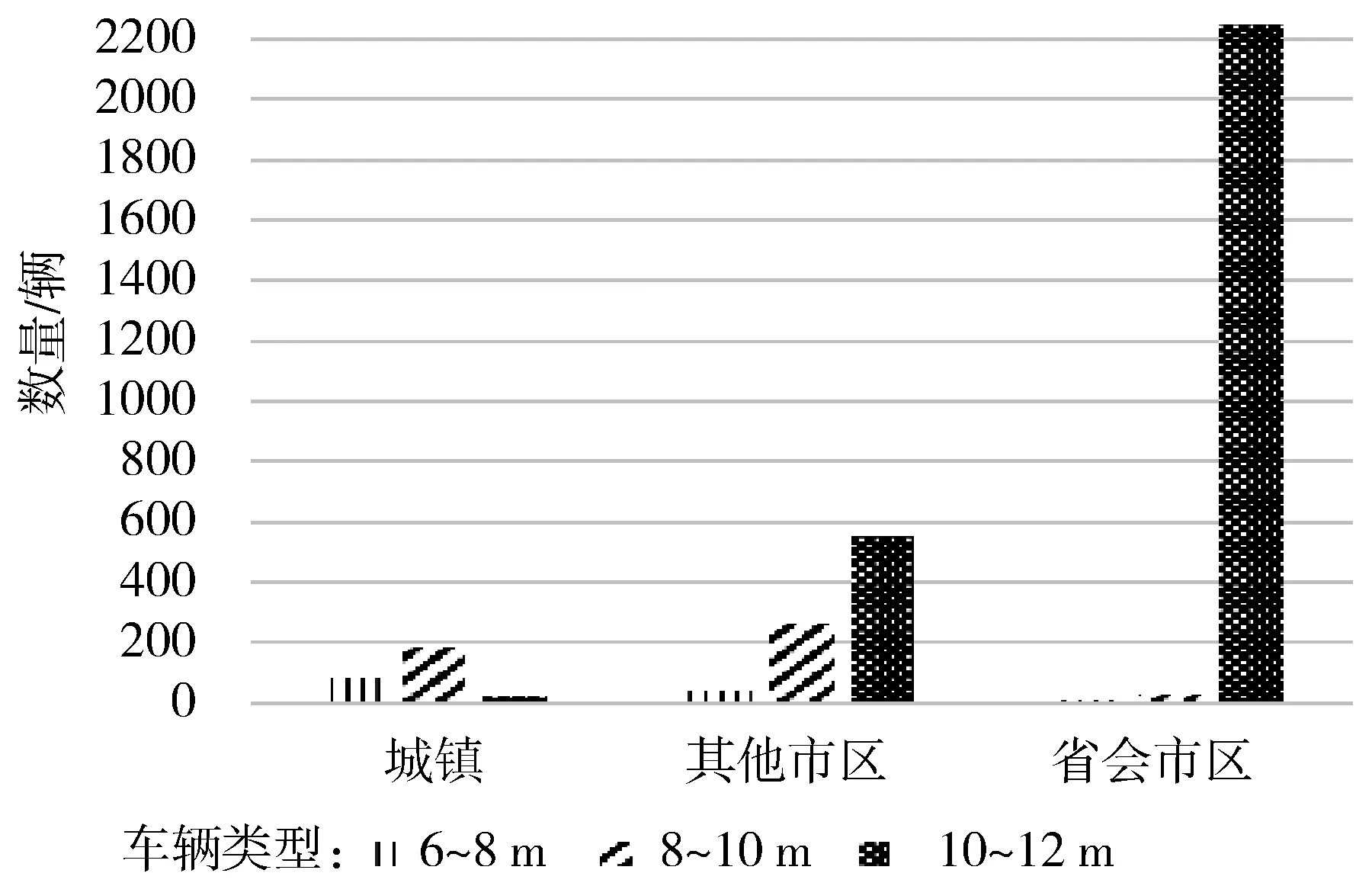
图4 城镇与市区的车辆类型

由图4可知，省会市区的新能源公交车基本上是大型车(10～12 m)，其他市区一半以上的新能源公交车是大型车(10～12 m)，城镇的新能源公交车基本上是以小型车(6～8 m)和中型车(8～10 m)为主。由此可以得出：市区的公交路线长，一般配备大型车；城镇的公交线路短，一般配备小型和中型车。

2.2.2 单因素方差分析

对以上数据进行方差分析，论证车辆的长度与年运营里程是否相关，即车辆的长度是否对车辆年运营里程有影响，分析结果如表2所示。其中：SS是离均差平方和，也就是变量中每个数据点与变量均值差的平方和；DF是自由度；MS是均方，其值等于对应的SS除以DF；F是F统计量，是方差分析中用于假设检验的统计量，其值等于处理的MS除以误差的MS；P-value表示在相应F值下的概率值；Fcrit表示在相应显著水平下的F临界值。

表2α=0.01时的方差分析结果

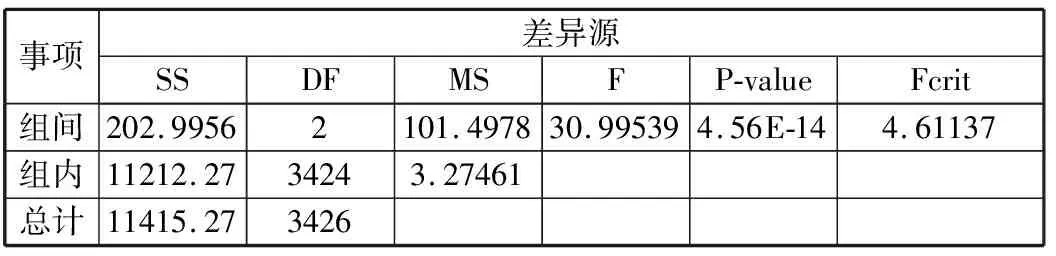
事项差异源SSDFMSFP-valueFcrit组间202.99562101.497830.995394.56E-144.61137组内11212.2734243.27461总计11415.273426

由表2可知，当组间的F=30.99539且Fcrit=4.61137时，有F>Fcrit，可以认为F在α=0.01的水平上极显著，即3组数据在α=0.01的水平上有极显著差异。由此可以得出结论，车长与车辆的年运营里程有一定的关系，故本文将新能源公交车的车长与年运营里程相结合来检测异常值。

2.2.3 运营里程申报数据异常值的界定

新能源公交车运营里程的影响因素主要有续航里程和公交路线。调研的过程中了解到，由于受续航里程以及公交线路的限制，新能源公交车的日运营里程一般不超过280 km(即年运营里程不超过1.022×105km)。故在做数据分析的过程中，可将该值(1.022×105km)作为经验值来标记训练集。

由2.2.1节可知，通常情况下，城镇的公交线路短，客流量小，配备的都是小型和中型新能源公交车(6～8 m和8～10 m的车型)，年运营里程相对较短；相比较而言，市区的公交线路较长，客流量大，配备的基本上是中型和大型新能源公交车(8～10 m和10～12 m)，年运营里程相对较长。根据数据的特点，结合线性SVM算法查找新能源公交车运营里程申报数据中的可疑值。

2.3 新能源公交车运营里程数据的异常值检测

2.3.1 训练SVM

从原始数据取同分布的训练集，训练集含100个类别，其中正类81个，负类19个。用训练集训练SVM算法，测试该算法分类器的性能。将函数SVC()中的参数C设置为0.1、0.5、1和3分别测试算法的准确率、特效度和检错率，测试结果如表3所示。

表3 测试结果

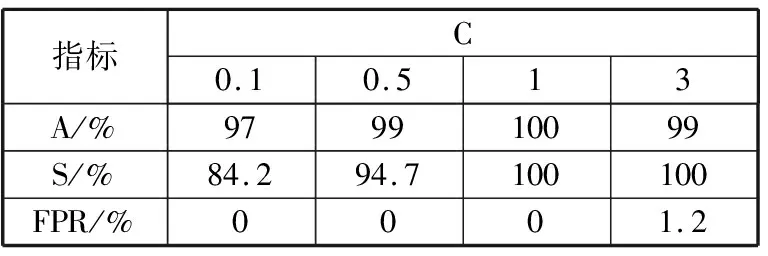
指标C0.10.513A/%979910099S/%84.294.7100100FPR/%0001.2

由表3可知，当C=1时，该算法的分类效果最佳，其准确率为100%，特效度为100%，检错率为0。测试结果表明，该算法用于检测新能源公交车运营里程申报数据的异常值是可行的。

2.3.2 检测异常值

选择2.1节中的3427辆新能源公交车年运营里程数据进行分析，利用线性SVM算法的线性核函数SVC(kernel=“linear”)，找最大间隔分离超平面，从而识别可疑值。

线性SVM算法在Python软件中检测异常数据的过程：首先导入相关的包，用训练集训练SVM算法；然后建立参数最优SVM分类器，即找出最大间隔分类器；最后将数据集分类，识别出可疑的数据。结果如图5和表4所示。

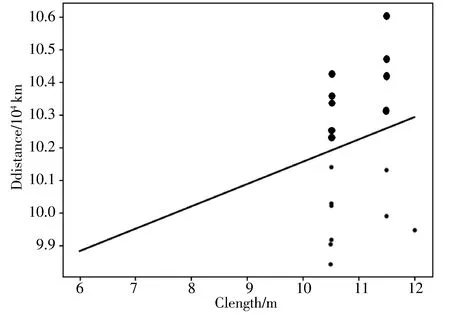
图5 检测结果部分数据图

表4 测试样本的详情

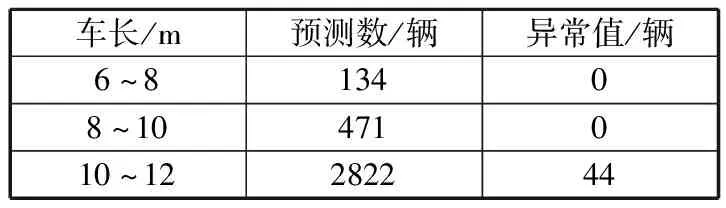
车长/m预测数/辆异常值/辆6～813408～10471010～12282244

线性SVM算法分类结果部分数据图如图5所示，横轴表示车辆长度，纵轴表是年运营里程，图中实线表示最大间隔分离超平面，该平面将数据集分为2类。图中实线以上数据表示运营里程异常值。

由图5可知，线性SVM算法在做数据分类时，考虑了数据集的整体分布情况，使得超平面尽可能地距离2类数据集的间隔最大，同时，该算法也充分考虑了对于不同的车型(车长不同)，其年运营里程存在差异的问题，即一般情况下，小型车辆的最大年运营里程不及大型车辆的最大年运营里程，算法准确率为99.8%，因此该算法的分类效果比较好。

由表4可知，该算法从3427条数据中找出了44条可疑数据。6～10 m和8～10 m车型的新能源公交车运营里程申报数据没有异常值，10～12 m车型的新能源公交车中存在44辆年运营里程可疑的车辆。异常值主要分布在车长为10.5 m和11.5 m的车辆中，运营里程申报数据在1.022×105km以上的10.5 m和11.5 m的车辆都是比较可疑的，这些值超过了新能源公交车正常的年运营里程。根据算法分类结果，从原始数据中查找对应的车辆，可将这些车辆作为新能源公交车运营里程实地核查的重点调查对象。

3 结束语

本文利用线性SVM算法从申报数据中筛选出可疑的数据，该算法能够考虑数据集的整体分布情况，通过训练好的SVM分类器将数据集分为2类，能够较准确地找出可疑车辆。研究结果表明，该算法能够考虑小型车相比大型的最大年运营里程车更小的情况，分类结果更加符合实际情况。

线性支持向量机适用于维数低的数据集，具有参数少、速度快和计算较为简单等优点，同时，支持向量具有较强的逼近能力和泛化能力。

本文只考虑了存量新能源公交车年运营里程数据的核查问题，对于少量增量新能源公交车未作分析，后续有待进一步研究。