一种面向工作负载预测的基于小波变换的特征提取方法

王 可，李 晖，陈 梅，戴震宇，朱 明

(1.贵州大学计算机科学与技术学院，贵州 贵阳 550025; 2.贵州省先进计算与医疗信息服务工程实验室，贵州 贵阳 550025; 3.中国科学院国家天文台，北京 100101)

0 引 言

时间序列数据在金融、工业、医药、科研等领域广泛存在，人们使用数据科学和机器学习技术对其分析进行可视化、决策和预测。时序数据是数据流的一种，且流数据挖掘具有量大、速度快、对数据仅扫描一次等特点，同时流数据挖掘是CPU密集型任务，易过载、高延迟。所以，在资源受限条件下实现最大化挖掘收益是一项艰巨的任务。因此，需要引入降载技术，降载(Load Shedding)[1-7]是指当输入数据流超出流处理引擎(Stream-Processing Engines, SPEs)[5,8-10]的处理能力时移除多余负载的过程。

降载策略主要包括随机降载[1,9]、语义降载[7]和自适应降载[1,3-5]。随机降载根据一定比例或随机丢弃一些元组，可能会丢失重要的元组。语义降载基于用户对数据流语义的理解，并使用可控的方法来抛弃不重要或相对不重要的元组。自适应降载引入一组服务质量(Quality-of-Service, QoS)[1,3,5]或决策质量(Quality of Decision, QoD)[2-3]规范，该策略对数据流及其运行环境的变化具有重要的适应能力，将降载问题转化为优化问题。

目前，降载的研究主要集中在数据流管理系统(Data Stream Management System, DSMS)[5]中的连续查询[1-2]和流数据挖掘[11]2大方面。降载的代表性工作如下：Tatbul等人[1]研究了可扩展和有效的SPEs降载技术。Babcock等人[3]提出在查询计划的不同位置引入降载操作符和降载程序。Gedik等人[8]提出一种针对加窗流连接的自适应CPU降载方法，旨在最大化流连接的输出速率。Chi等人[2]引入QoD规范来度量由降载引起的无法准确获得数据的特征值时分类结果的不确定性程度。陈华辉等人[12]提出H-WAS-clustering算法，该算法利用小波变换系数来计算距离和划分数据，对多个数据流进行聚类、压缩数据，降低了空间和时间复杂度。时间序列建模是研究历史时间序列，以建立适当的模型来描述该序列的固有结构，然后利用该模型预测该序列未来的值。自回归差分移动平均(AutoRegressive Integrated Moving Average, ARIMA)模型是最常用的随机时间序列模型之一[13-14]。

在本文工作中，使用DTW距离度量子序列与整个序列之间相似度的变化以确定用于预测的数据，然后利用小波变换计算小波系数并提取小波系数的能量值作为预测的特征，最后预测任务执行时间。预测数据挖掘任务执行时间的实验结果表明该方法有较高的准确性。

1 小波变换和特征提取

1.1 小波变换

小波变换[10,15-20]是一种层次分解序列的时域变换技术，是一种时频局部化或时频定位的工具，其良好的多分辨率特性特别适用于对非平稳信号分析和处理及构造数据摘要。小波的特点是在近似部分保留输入序列的大趋势，而在细节部分保留局部变化。Haar小波是小波分析发展过程中出现最早的小波，其实质上是一阶的Daubechies小波，也是最简单的具有紧致特性的显式正交小波。其母小波函数和尺度函数定义如公式(1)和公式(2)所示：

(1)

(2)

规范化的Haar小波尺度函数如公式(3)：

(3)

其中j为尺度因子，改变j使函数图形缩小或放大；i为平移参数，改变i使函数沿x轴方向平移；常数因子用以满足内积等于1的条件。

1.2 特征提取

特征提取是指从数据中提取有用特征的降维或函数映射过程[21]。特征提取、选择和构造是选择数据或实例等数据简约的有效方法，其目标是：1)减少数据量；2)关注相关数据；3)提高数据质量。要提高挖掘算法性能，主要依靠挖掘算法或在挖掘前进行预处理2种方法。

时间序列[18]的应用中有多种特征提取算法，如奇异值分解(Singular Value Decomposition, SVD)、离散傅里叶变换(Discrete Fourier Transform, DFT)和离散小波变换(DWT)等。SVD计算的时间复杂度很高，DFT和DWT都是具有快速的计算算法的信号处理技术，DWT将原来的时间序列从时域转换为频域，再由频域转换为时频域[18]。小波变换时间序列的时频局部化特性意味着时间序列的大部分能量可以用几个小波系数来表示。

2 Wavelet-based特征提取算法

任务执行时间不仅与任务参数相关，还与执行过程中的其他数据密切相关，如服务器的资源状态数据(CPU、I/O、内存和系统负载等)、任务状态数据等。结合任务执行过程中的任务参数和状态数据预测任务执行时间可以得到更好的结果。算法分为2阶段：1)引入参数度量降载时间点；2)利用小波变换进行特征提取。

2.1 度量降载时间点

时间序列有很强的连续性，不适合进行分段处理。分析时间序列数据，不仅要关注某一点，还要关注连续点和连续序列的特征，如均值、方差、偏度、峰度、波动性等。这些点形成一个窗口或向量，窗口的大小随着数据的增加而增加；然而，连续时间序列中大多数数据点不是独立的而是相互关联的，因此会存在一定的信息冗余，所以对多个窗口预测并不合适[11]。使用任务执行期间不同数据进行预测，结果差异非常大，所以需要度量预测所使用的数据。

整个序列记为X(X=〈x1,x2,…,xi〉)。引入参数α(α∈(0,1))来衡量预测的位置，参数α将整个序列X等分为i个子序列，使用DTW距离[20,22-24]测量子序列和整个序列的相似度。参数α定义如公式(4)，其中length()表示序列的长度。Qj为从原序列初始位置取特定比例后的子序列，其定义如公式(5)，其中j∈[0,i],j∈Z。

α=length(xi)/length(X)

(4)

Qj=〈p0,p1,…,pj〉

(5)

设时间序列X、Y的DTW距离为D(X,Y)，定义如公式(6)所示，其中，Dbase(xi,yi)表示向量点xi和yi之间的基距离，记D0(xi,yi)为D0。可以根据情况选择不同的距离度量，为不失一般性，使用欧氏距离作为基距离。

(6)

使用相似度的变化来度量降载的时间点：通过捕捉时间序列相似性的变化，实现序列相似度变化的离散化并度量预测的时间点。因相似度距离的变化是连续的，如果对每个时间点都进行计算会导致复杂度太高，因而对参数α进行多窗口大小局部平均处理，这样可以离散化时间序列相似度的变化。算法1展示了度量降载时间点算法的细节。

算法1度量降载时间点。

输出: 参数α的取值范围

1: forl=1 tomdo

2: forj=1 toido

3:Qj=〈p0,p1,…,pj〉

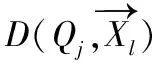
6: end for

7: end for

8: for策略t∈window,l∈[1,m]do

9: 根据策略t将distancel划分为n部分，距离结果集记为{re}

10: 归一化{re}到[0,1]范围内

11: 根据不同窗口大小window策略统计频繁模式

12: 返回参数α的取范围

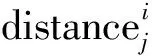
该策略记为window(win)(win是窗口的大小)，根据窗口的大小定义3种策略取3种窗口内的平均值来捕捉序列相似度变化模式的分割方法，如公式(7)所示：

(7)

为比较不同序列以及获得不同策略下所有数据的变化模式，将每种策略的相似度距离计算结果进行归一化，将最小值和最大值映射到[0,1]。模式集中位置i处的模式定义如式(8)，其中h、m、l分别表示High、Middle、Low：

A=〈A1,A2,A3〉,Ai∈{h,m,l}

(8)

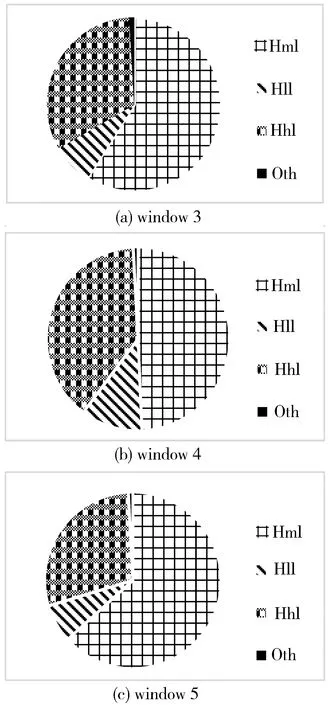
图1 不同窗口大小下模式集的占比

模型集A在3个位置上的组合模型共27个(33)。通过对结果集进行处理和分析，频繁模式主要集中在以下模式中，这些模式随α增加相似度距离变化的趋势可划分为以下模式集，包括Hml(〈h,m,l〉)、Hhl(〈h,h,m〉,〈h,h,l〉,〈m,m,l〉)、Hll(〈h,m,m〉，〈h,l,l〉,〈m,l,l〉)和Oth，统计结果如图1所示。Hml表示相似度逐渐增大的模式；Hhl表示相似度先稳定后增加的模式集；Hll表示相似度先增加后稳定的模式集；Oth表示剩余的没有共同特征的模式集。图1是模式集的特征与分析统计结果，取所有数据序列的平均值作为最终结果。

不同大小的窗口下模式集的占比结果如图1所示，超过90%的数据显示出明显的下降趋势。图2显示stage1阶段相似度的变化较快，stage3阶段相似度的变化较缓，在stage2与stage3序列的相似度更高。通过统计模式集Hml与Hhl距离的变化，可以得出结论：与stage1相比stage2部分子序列与整个序列的距离明显减小。

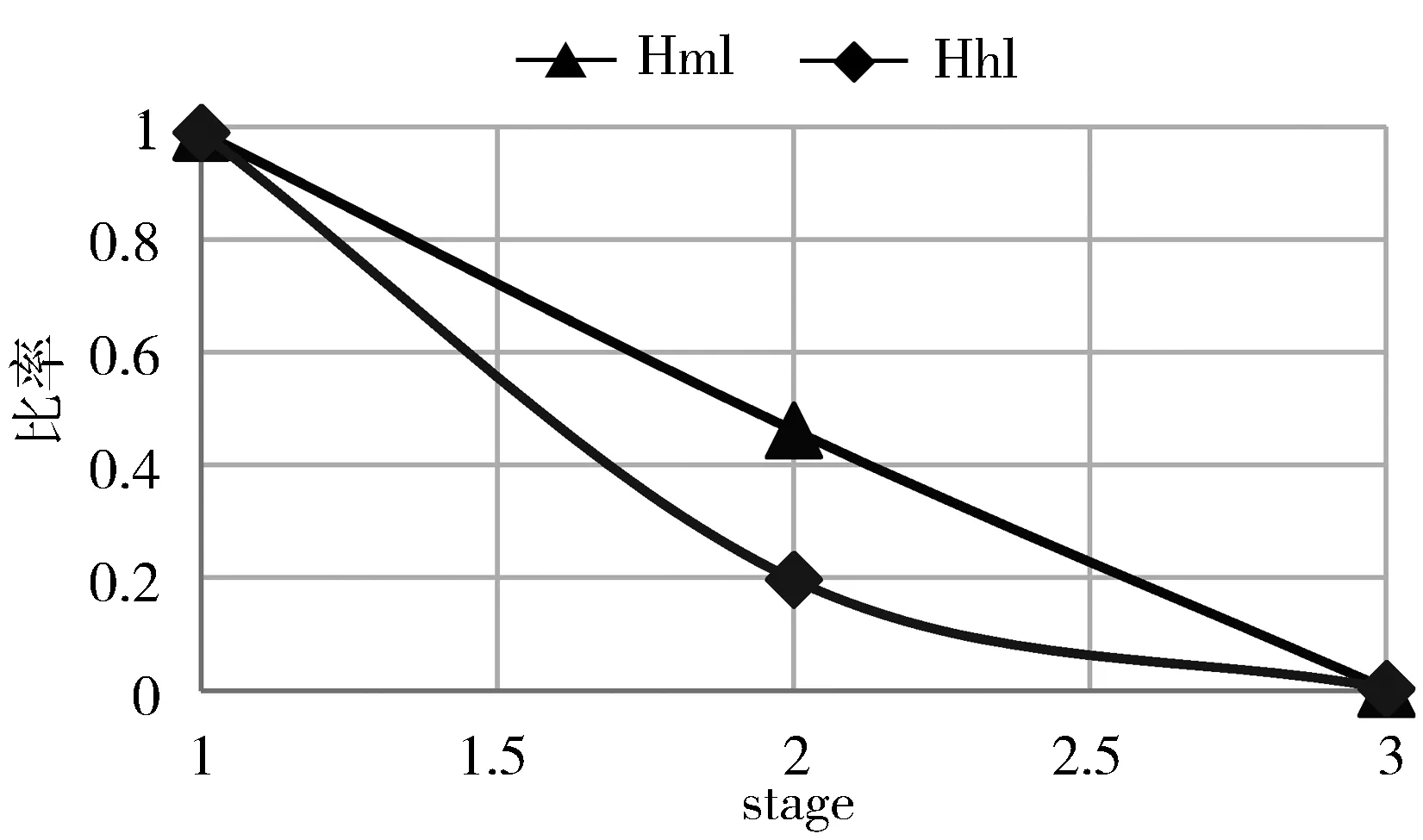
图2 模式集Hml和Hhl距离的变化

数据挖掘任务的主要操作部分耗时较多且占用CPU资源较多。根据图1中相似度变化的统计分析结果和任务执行日志分析结果，stage3阶段任务多位于预测、可视化和保存数据阶段，该部分不会持续占用较高的CPU资源，而在stage1和stage2阶段任务多位于比较消耗CPU的核心操作阶段(核心操作AutoML、k-Means、GBDT阶段)，从任务开始时选取特定比例(α)的数据用于预测，该部分包含了资源指标数据相对于全部数据中相似度变化较大的部分，说明该部分数据包含了较多的变化信息，所以选取这部分数据用于预测可以降低预测的误差。在α∈[0.3,0.7]或α∈[0.4,0.6]时子序列与原序列相似度的变化较大且包含相似度距离变化较快的stage1、stage2阶段，根据以上分析结果，选择stage2进行预测更为合适。

2.2 Wavelet-based特征提取算法

根据2.1节中确定的α的取值范围以及用于预测的数据，提出一种面向预测基于小波变换的特征提取方法。

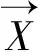
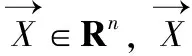
(9)

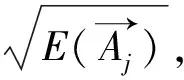
算法2Wavelet-based特征提取方法。

输出: 时间序列在不同尺度上的特征

1: fori=1tomdo

2: 使用Haar小波计算时间序列最大尺度J

3: 将不够长度2j的时间序列补0

4: forj=0 toJ-1 do

7: end for

8: end for

3 实验结果和评估

3.1 实验设置

负载。本实验中的工作负载包括一系列基于工作流的数据挖掘(DM)和ETL任务。DM任务主要包括输入、AutoML、K-means、GBDT、采样、预测、数据可视化、结果保存等操作，主要操作是CPU密集型任务，其数据集是UCI数据集，因标准数据集数据量小，需要扩增数据量(150～100000)，使DM任务可达到高负载状态。用Java程序调整用户数来控制任务并发，并设置采样器的参数来控制数据量和任务中训练集与测试集的比例等。ETL任务包括使用TPC-H数据集进行转换、连接等操作，此任务主要用于调整服务器可用CPU、内存和I/O资源状态。本文使用多种数据收集方法(包括流数据处理方法，如Kafka)收集任务属性数据、服务器资源状态数据和任务状态数据。

本文使用随机森林算法来评估基于任务参数方法(Task-parameters)和以下3种特征提取方法(Statistical, Wavelet-based, Wavelet-sta)的预测结果。为了得到更可靠实验结果，采用5折交叉验证法，即将数据集平均分成5份，随机选择其中1份作为测试数据，其余的作为训练数据，并且取5次的平均值作为最终的结果。Task-parameters：使用任务数据量、并发数、主要操作的重要参数作为特征。Statistical：计算时间序列的一阶原点矩(均值)、二阶中心矩(方差)和三阶中心矩(偏度)作为统计特征。Wavelet-based：利用第2章提出的基于小波变换的特征提取方法提取时间序列特征。Wavelet-sta：将Statistical与Wavelet-based方法相结合提取时间序列特征。

3.2 预测结果

根据任务数据量、并发数、主要操作的重要参数(迭代次数、学习率、树的数量、训练集测试集比例(数据挖掘任务中训练集测试集比例))将数据集划分为D1和D2，主要原则是保证划分的数据集有一定的区分度以及保证划分的数据集在进行实验时训练集和测试集中不会出现重复数据。其中，任务执行时间从几十秒到1600 s不等，平均执行时间约400 s。为验证不同特征提取方法的预测结果的准确性，使用均方根误差(RMSE)、平均绝对误差(MAE)和确定系数(R2，回归中R2是回归预测与真实数据近似程度的统计度量)来验证随机森林算法的准确性。

Task-parameters方法在数据集D1和D2的预测结果评估指标如表1所示。3种特征提取方法在数据集D1、D2与参数α条件下的预测结果的评估指标如表2所示。

表1 仅使用任务参数在数据集D1和D2预测结果的评估指标

DatasetMethodsRMSEMAER2D1Task-parameters1281030.38D2Task-parameters12798.30.667

比较不同参数和数据集的预测结果，可以得出以下结论：仅使用任务参数在数据集D1和D2的预测结果误差较大且与原始数据吻合度较低；在任务执行过程中使用资源和任务参数数据的可以很大程度减少预测误差。在相同数据量的情况下，Wavelet-based方法和Wavelet-sta方法比Statistical方法可得到更好的效果。从表1和表2可以得出，在相同的数据集下这3种特征提取方法的预测误差比使用Task-parameters方法要小很多。

表2 3种特征提取方法在数据集D1和D2与参数α条件下预测结果的评估指标

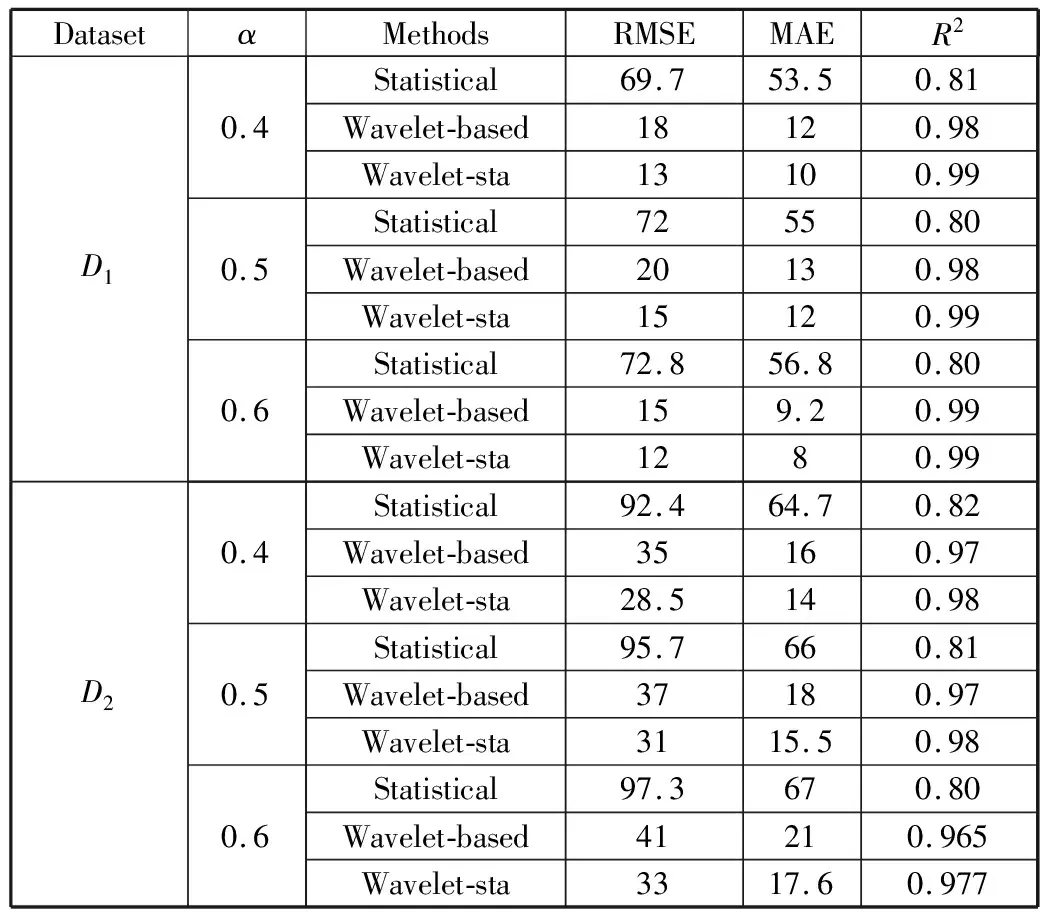
DatasetαMethodsRMSEMAER2D10.40.50.6Statistical69.753.50.81Wavelet-based18120.98Wavelet-sta13100.99Statistical72550.80Wavelet-based20130.98Wavelet-sta15120.99Statistical72.856.80.80Wavelet-based159.20.99Wavelet-sta1280.99D20.40.50.6Statistical92.464.70.82Wavelet-based35160.97Wavelet-sta28.5140.98Statistical95.7660.81Wavelet-based37180.97Wavelet-sta3115.50.98Statistical97.3670.80Wavelet-based41210.965Wavelet-sta3317.60.977

表2中，比较当数据集为D1、α=0.4时RMSE与MAE的数值可得出如下结论：Wavelet-based和Wavelet-sta方法比Statistical方法有更小的预测误差；比较R2可以得出Wavelet-based和Wavelet-sta方法预测结果与原数据拟合效果比Statistical方法好很多。比较当数据集为D1、α=0.4时RMSE、MAE与R2的数值，Wavelet-sta方法的预测结果比Wavelet-based有一定程度的提升。因此，将Statistical与Wavelet-based方法相结合可以进一步降低预测误差。表2中数据集为D1时，实验结果的RMSE和MAE相对于比Task-parameters方法有很大程度的减小，同时R2提高了很多；随着α的增加，结果误差和拟合系数都在较小的误差范围内波动。当数据集为D2时，可以得到以上类似的结论。综合以上结论，新提出的特征提取方法是有效的；在预测结果方面，降低了误差，显著提高了预测结果与原始数据的拟合程度，验证了特征提取方法和降载策略的有效性。

4 结束语

在分析型系统任务执行过程中，任务执行时间不仅与任务参数相关，而且与执行过程中的约束条件(如资源利用率、任务状态数据)密切相关。在任务结束后进行任务执行时间预测毫无意义，需要在任务执行前或执行过程中进行预测。在任务执行过程中，结合状态数据和任务参数来预测任务执行时间可以得到较好的结果。本文使用DTW距离来度量子序列和整个序列之间的相似性变化，从而确定用于预测的数据和时间点；利用小波变换计算时间序列的小波系数，提取小波系数的能量值作为预测的特征。数据挖掘任务执行时间预测真实场景的实验结果表明了该策略的有效性。