计及等效转动惯量的储能最优调频控制方法

郄朝辉，黄 慧，陆承宇，马骏超，胡 阳

（1.南瑞集团有限公司（国网电力科学研究院有限公司），南京 211106；2.国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

我国资源和负荷逆向分布的特点决定了未来能源开发以西北部能源基地集中开发、远距离送电为主，东中部就地开发作为补充[1]。随着新能源的不断开发和利用，预计到2035 年新能源占总装机比例将由2017 年的17%提高至38%。随着风电、光伏等新能源发电占比不断提高，系统总转动惯量不断降低，电网频率调节能力呈下降趋势，在大功率缺额情况下，极易引发频率越限甚至系统失稳，给电网安全稳定运行带来挑战。因此，需要更多控制措施和手段保证电网持续安全高效运行。

储能系统能够为电网运行提供调峰、调频、备用、黑启动、需求响应支撑、提高新能源消纳能力[2-7]等多种服务，是提升传统电力系统灵活性、经济性和安全性的重要手段，未来储能系统将在电网大规模广泛应用[8-9]。

在系统调频方面，储能系统具备快速的双向功率控制能力[10-14]。储能参与电网调频后，通过电网惯性变化分析储能系统功率控制对电网频率变化的抵抗，从根本上研究储能对系统频率变化的影响，是实现电网频率控制的最优控制方法。但目前基于储能系统等效惯量如何表征，还缺少相关的理论方法。因此，研究储能系统的等效转动惯量是十分必要，也是十分有益的。

文献[11]分析了储能系统参与电网调频的技术优势。文献[12]提出了一种储能装置提供一次调频成本最小的优化配置方案。文献[13]提出了一种计及SOC（荷电状态）自恢复需求的储能与传统机组参与二次调频的策略。本文根据频率变化等效原则，研究了储能系统的转动惯量计算方法，并比较了典型控制方式下[15-16]转动惯量的特性和区别，得出储能系统典型控制方式的应用场景，给出一种储能系统的最优调频控制方法。最后建立了仿真验证环境，对不同控制方式下的储能转动惯量进行分析，研究频率变化不同阶段不同控制方法转动惯量变化趋势，验证了理论分析的正确性及最优调频控制方法的有效性。

1 储能系统等效转动惯量

1.1 电网转动惯量

惯性是物体对象对其速度变化的抵抗，这种特性是物体在没有外部作用的情况下保持当前运动状态的能力。在直线运行物体中，质量是惯性的表征量。在旋转物体中，转动惯量是惯性的表征量。转动惯量在旋转动力学中的角色相当于线性动力学中的质量。

同步电网是一个主要由旋转电机提供旋转惯量的巨大惯性系统，电网频率变化率主要表征为发电机和电动机及其拖动的转动机械的转动惯量。因此，在电力系统中，转动惯量一般为衡量电网频率变化率的主要指标，具体表示为不平衡转矩引发的电机转子旋转速度的变化。

根据旋转物体力学定义，同步发电机转子的机械角加速度与作用在转子轴上的不平衡转矩有如下关系：

式中： J 为转子的转动惯量；Ω 为转子机械角速度；α 为机械角加速度；ΔM 为作用在转子轴上的不平衡转矩；ΔP 为不平衡功率；PD为阻尼功率。

一般情况下认为，电网频率为全网特性，各发电机转子感受到的频率一致。因此如式（3）所示，每个同步发电机的转动惯量可直接相加，等效为一台发电机转子提供旋转惯量。

式中： N 为电网同步电机数量；Ji，ΔMi，ΔPi（i=1，2，…，N），PDi（i=1，2，…，N）分别为不同同步发电机的转子转动惯量、不平衡转矩、不平衡功率和阻尼功率；ΔP 为系统不平衡总功率；PD为系统总阻尼功率。

1.2 储能系统等效转动惯量

储能系统接入电网中，输出或吸收功率对电网频率产生影响。在忽略负荷随频率变化特性、损耗和调速器等因素影响前提下，系统原有功率缺额不变的情况下，储能系统能量输出影响转子动能（，其中ω 为转子角频率）变化。转子动能与角频率成二次方关系，储能系统输出功率约等于转子动能差值，因此相同功率输出的储能系统提供的等效转动惯量与系统原有频率相关。

建立单机系统和储能的简单模型，由式（1）、式（2）可知，系统转动惯量和不平衡功率的关系为：

考虑储能系统输出功率Pa，则式（4）变为：

储能系统功率输出后，系统频率变化率发生改变，可表征为电网转动惯量动态改变。为研究储能系统给电网带来额外的等效转动惯量，设置系统等效转动惯量为J′，则式（5）可等效为：

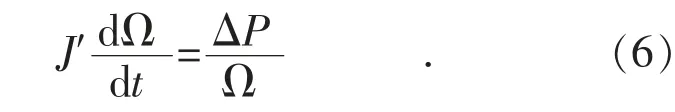
转子机械角速度Ω 与电网频率的关系为：

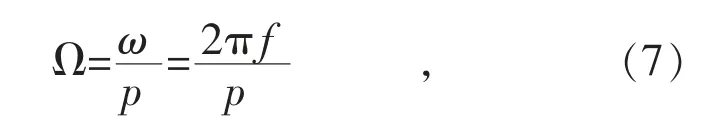
式中： p 为同步发电机转子的极对数，电网结构不变时为常数；f 为当前电网频率。

系统阻尼功率和系统频率的关系为：

式中： D 为阻尼功率系数；f0=50 Hz，为正常电网频率。

由式（5）—（8）可知，储能系统和阻尼功率提供的额外等效转动惯量ΔJ 为：

式中： f′为系统频率变化率；ΔJC为储能系统提供的转动惯量；ΔJD为阻尼功率提供的转动惯量。

由式（9）可知，系统阻尼、储能系统均对系统提供额外转动惯量，且提供的转动惯量具有可加性。

式（9）表明，储能系统提供的转动惯量和系统原有特性耦合，与电网实时频率和频率变化率相关。由于电网频率f 在50 Hz 附近变化不大，p为常值，因此储能在提供相同功率的情况下，电网频率变化率越小，提供的转动惯量越大。原电网转动惯量越大，则频率变化率越小，储能系统能够提供更多等效转动惯量，体现了储能系统提供转动惯量“遇强则强”的特性。

储能系统根据电网频率、电压等指标响应或内部控制实现对电网发送或吸收功率，影响电网频率变化。因此，储能不同功率控制方式会给系统带来不同的额外转动惯量。

1.3 储能下垂控制转动惯量特性

储能系统采用下垂控制时，功率输出等效为一阶惯性环节[17]，输出功率Pb为：

式中： K 为储能系统下垂控制比例系数；T 为储能系统控制响应时间常数，一般取100 ms。

因此，加入储能下垂控制后的不平衡功率方程为：

则储能等效转动惯量ΔJ1为：

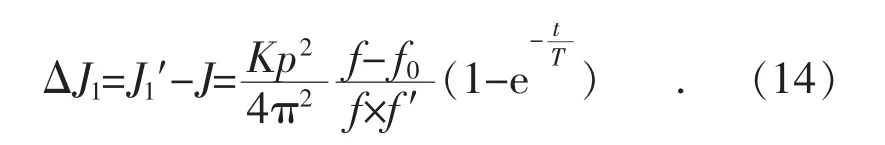
由式（14）可知，在电网频率破坏阶段（系统频率逐步偏移50 Hz）时，频率差（f-f0）和频率变化率f′符号一致，下垂控制能提供正转动惯量，降低频率偏离50 Hz 的程度。电网频率恢复阶段（系统频率逐步接近50 Hz），频率差（f-f0）和频率变化率f′符号相反，下垂控制能提供负转动惯量，加快系统频率恢复。因此，不论是在系统频率下降还是上升时，储能系统下垂控制方式能够自适应提供系统最适宜的额外转动惯量，具有良好的自适应控制特点。

根据式（14），忽略储能最大功率输出，在电网频率变化率不变或变化较小时，储能下垂控制后的等效转动惯量ΔJ1约等于：

由式（15）可知，电网频率变化率不变时或变化较小时，储能在不同电网频率变化率情况下提供的惯量基本相同，与时间成正比。因此，在频率变化不大时，储能惯性控制随着时间增加，能够提供更多的等效转动惯量。

考虑到储能系统输出功率Pb满足-Pbmax≤Pb≤Pbmax，令为储能系统下垂控制最大功率后的等效转动惯量，则系统等效转动惯量ΔJ2为：

根据式（16），储能系统提供最大功率后，在频率变化率不变的情况下，储能系统提供的转动惯量和系统频率变化率相关，系统频率变化率越小，储能系统能够提供更大的转动惯量。

考虑储能系统频率控制死区fzer0=0.033（参考常规发电机一次调频死区），最大功率输出1 kW，系统功率缺额后频率上升，在不同电网频率变化率情况下，计算储能系统提供的等效转动功率如图1 所示（频率变化率参考江苏2015 年9 月19日锦苏直流双极闭锁12 s 后，频率跌至49.56 Hz）。

图1 储能系统下垂控制等效转动惯量

由图1 可知，储能系统采用下垂控制时，在达到最大等效转动惯量前，不同频率变化率情况下，储能系统提供的转动惯量基本相同。储能最大输出功率不变时，系统频率变化变化率较小，储能系统能够提供更多的最大转动惯量。

1.4 储能虚拟（负）惯性控制

储能系统采用虚拟惯性控制时，其中ME为正值，输出功率Pc为：

因此，加入储能系统虚拟惯性控制后的不平衡功率方程为：

则加入储能系统虚拟惯性控制后，等效转动惯量变化ΔJ3为：

由式（20）可知，在频率破坏阶段或恢复阶段，储能系统虚拟惯性控制能够增加系统惯量，在频率破坏初始阶段有利于降低频率偏移程度；在频率恢复阶段，增加系统惯量不利于频率快速恢复。

同理，储能系统采用虚拟负惯性控制时，其中ME′为正值，输出功率Pd为：

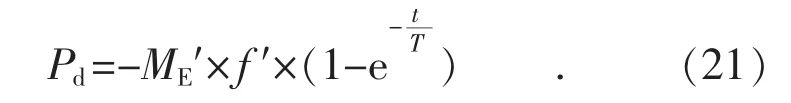
则加入储能系统虚拟负惯性后，等效转动惯量变化ΔJ4为：

由式（22）可知，在频率破坏阶段或恢复阶段，储能系统虚拟负惯性控制能够降低系统惯量，在频率破坏阶段不利于降低频率偏移程度；在频率恢复阶段，降低系统惯量有利于频率恢复。

考虑储能系统频率控制死区fzer0=0.033，最大功率输出1 kW，系统在不同频率变化率情况下，储能系统提供的等效转动惯量如图2 所示。

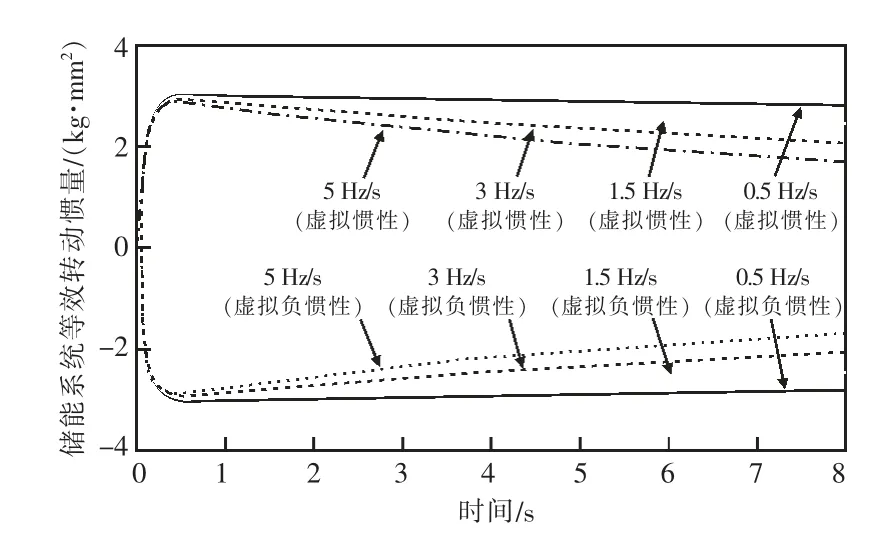
图2 储能系统虚拟惯性/负惯性控制等效转动惯量

由图2 可知，在储能系统采用虚拟惯性控制方式时，能够快速提供最大输出惯量，有利于快速降低频率偏离程度；而虚拟负惯性控制方式提供最大负惯量，使频率偏离程度增加。因此，储能系统采用虚拟惯性控制，有利于抑制频率破坏；采用虚拟负惯性控制时，有利于加快频率恢复。在频率不同变化阶段时，应采用不同的惯性控制方式，更有利于电网频率调节。

2 储能系统最优控制方法

为尽可能维持稳定、安全的电网频率，系统功率缺额不变时，在频率破坏初始阶段需要增加系统惯性以控制频率不产生较大偏差，在频率恢复阶段需要降低系统惯性以加速频率恢复。

因此，在系统频率破坏阶段需要提高系统惯量，系统频率变化较大时，应采用虚拟惯性控制最大程度增加系统惯量，降低频率偏差。在系统频率较快恢复过程中，应采用虚拟负惯性控制方法最大程度降低系统惯量。在频率变化其他阶段应采用下垂控制方法，自适应频率破坏和恢复阶段惯性控制要求。因此，最优控制方法如下：

式中： Pz为储能系统最优控制方法有功功率控制输出，Pz＞0 储能发出功率，Pz＜0 储能吸收功率，其他情况时储能与系统交换功率为零。S1，S2，S3，S4 为频率变化的不同阶段。具体计算方法为：

式中： Δdf 为频率变化率转换定值，可根据储能系统功率输出与系统惯量综合决定。

3 仿真分析

建立小容量的发电机-负荷-储能系统，研究储能系统不同控制方式下的电网频率恢复特性和提供的转动惯量。系统在0 s 发生功率缺额，功率缺额80 MW，发电机动能为20 MW·s，储能系统最大输出功率为10 MW，控制响应时间常数为100 ms。储能系统下垂控制比例系数K 为10 MW/Hz，虚拟（负）惯性控制系统ME和ME′均取50 MW·s/Hz。仿真电网在持续频率缺额的情况下，分析储能系统不同控制方式下，抑制频率偏差能力和提供的等效转动惯量值。

如图3、图4 所示，在频率破坏初始阶段，虚拟惯量控制提供最大的惯量，3 种控制方式中频率变化率最小。虚拟负惯量控制提供负惯量，3种控制方式中频率变化值最大。其后在频率达到极值之前，下垂控制提供的惯性逐渐增大。在频率恢复阶段，下垂控制提供了最大负惯性，频率恢复最快。虚拟惯性控制提供了正惯性，不利于频率恢复。

图3 储能系统不同控制方式的频率过程

图4 储能系统不同控制方式实际功率输出

如图4 所示，在频率破坏初始阶段，系统频率变化率较大，虚拟惯性/负惯性控制输出功率瞬间达到最大，下垂控制方式输出功率缓慢增加。在12 s 后，系统频率偏差变小，根据下垂控制参数，输出功率下降。在频率恢复阶段，频率变化缓慢，而频率偏差较大，下垂控制方式输出更多功率，有利于频率恢复。

如图3 所示，采用储能系统最优控制方法，最大频率偏差最小，频率恢复速度最快，相对于下垂控制和虚拟（负）惯性控制，具有较好的控制效果。

4 结论

储能系统对电网输出或吸收功率，通过功率交换实际上提供了系统额外等效惯量。根据转子运动方程，计算了频率变化时输出功率和等效转动惯量的关系。根据储能系统典型控制方式，计算了不同控制方法下储能系统等效转动惯量的特性。

由于惯量为衡量电网频率变化率的主要指标，根据下垂控制和虚拟（负）惯性控制提供等效转动惯量的特点，储能系统控制应最大程度控制系统频率偏差，加速频率恢复。

（1）在频率破坏初始阶段，频率变化率较大、频率偏差小时，应采用虚拟惯性控制快速提供大转动惯量抑制频率偏移程度。

（2）在频率接近最大频率偏差、频率变化较小时，应该采用下垂控制提供更多等效转动惯量。

（3）在频率恢复阶段，应降低系统惯性提高频率恢复速度，不能采用虚拟惯性控制： 频率偏差较大时，应采用下垂控制；频率变化率较大时，应采用虚拟负惯性控制。

结合储能系统不同控制方法提供的转动惯量特性，及转动惯量与系统频率的关系，提出了储能系统的最优控制方法。

仿真建立了发电机-负荷-储能模拟系统，系统在发生大功率缺额时，分析了不同控制方式的储能系统提供等效转动惯量的变化规律和对频率的影响。仿真结果验证了理论分析结果的正确性及最优调频方法的有效性。