FLS-based fault-tolerant control for an unmanned marine vehicle with actuator faults

(Department of Foundational Courses, Shenyang Institute of Science and Technology, Shenyang 110167, China)

Abstract: This paper is concerned with the fuzzy fault-tolerant control problem for an unmanned marine vehicle with actuator faults. The unmanned marine vehicle model is established as a linear system with matched unknown nonlinear uncertainty. The actuator faults considered in this paper contain the loss-of-effectiveness fault and outage fault. Besides, the unknown nonlinear function is approximated by using the fuzzy logic system. By estimating the norm of the weight vector in the fuzzy logic system, the number of adaptive parameters is reduced effectively. Furthermore, an appropriate adaptive update rate is designed to update the adaptive parameters in real-time. Based on the adaptive parameters of the design, the fuzzy fault-tolerant controller is constructed. Compared with the existing fault-tolerant control results, a novel controller is developed by introducing a switching mechanism in the controller. By introducing the switching mechanism in the controller, the developed controller can avoid the chattering phenomenon, which may occur in the existing controller. Furthermore, by using the Lyapunov stability theory, it is proven that the uniformly ultimate boundedness can be achieved by the developed method. Finally, a simulation example is used to demonstrate the efficiency and effectiveness of the developed approach.

Key words: fault-tolerant control; fuzzy logic system; unmanned marine vehicle; adaptive control

0 Introduction

Unmanned marine vehicle (UMV) has been applied in many fields such as environmental monitoring, military operations and oil and pollution clean-up[1-3]. Motion control problems of unmanned marine vehicles have received a lot of attention owing to the increasing demand for high reliability and of practical applications[4-8]. In[9], the authors model the UMV by a network-based modelling and then develop a dynamic output feedback control method under network environments. However, the linear model is established in[9]. It is well known that the nonlinear is usually existing in the UMV. Thus, this paper establishes a nonlinear model for UMV. On the other hand, actuator faults are unavoidable in practical applications[10-12].Thus, it is also necessary to develop a fault-tolerant controller to compensate for the influence of actuator faults for the UMV.

In this context, this paper aims to concern with fuzzy fault-tolerant control problem for an unmanned marine vehicle with actuator faults. This paper is the first trial to establish the unmanned marine vehicle as a linear system with matched unknown nonlinear uncertainty. By using the fuzzy logic system to approximate the nonlinearity, a novel fuzzy controller with fault-tolerant function is developed to compensate for actuator faults. The number of adaptive parameters is reduced effectively by estimating the norm of the weight vector in the fuzzy logic system. Furthermore, it is proven that the developed method can guarantee the state of the closed-loop system is the uniform ultimate boundedness (UUB). Finally, the validity of the developed method can be shown by a simulation example.

1 Unmanned Marine Vehicles System

1.1 Modelling of an Unmanned Marine Vehicle

This paper considers the earth-fixed and body-fixed reference frames as Fig.1. WhereX,Y, andZare earth-fixed reference frames.X0,Y0, andZ0are body-fixed reference frames.

Fig.1 Reference frames of a unmanned marine vehicle

As described in[9], the body-fixed equations of an unmanned marine vehicle system are given by

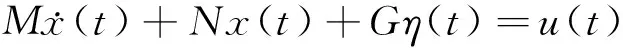
(1)

where

x(t)=[α(t),β(t),γ(t)]T∈R3,η(t)=[xp(t),yp(t),φ(t)]T∈R3andu(t)=[u1(t),u2(t),u3(t)]T∈R3.xp(t)∈Randyp(t)∈Rare the positions.φ(t)∈Ris the yaw angle andα(t)∈R,β(t)∈Randγ(t)∈Rrepresent the surge, sway, and yaw velocity, respectively.u1(t)∈R,u2(t)∈Randu3(t)∈Rdenote the force in surge, the force in sway and the moment in yaw.M> 0,NandGdenote the matrix of inertia, the matrix of damping and the matrix of mooring forces.

In addition, the dynamic ofη(t) is given by

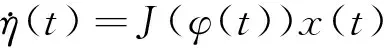
(2)

where

(3)

LetA=-M-1N,B=M-1. Hence,

(4)

whereg(·)=Gη(t).

As mentioned in[9], the yaw angleφ(t) can be chosen small enough, we havecos(φ(t))≈1, sin(φ(t))≈0 and the variableη(t)can be seen as a function of variablex(t). Hence, the nonlinear functiong(·) can be seen as a function of variablex(t),i.e.,g(·)=g(x(t)). Thus, the system (4) can be rewritten as

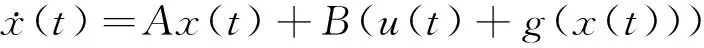
(5)

1.2 Fault Model

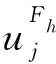
(6)

Denote

(7)

For simplicity, the following fault models are considered:

uFh(t)=ρhu(t),

(8)

whereρ∈{ρ1,…,ρH}

Similar to the existing FTC results[13-14], the following assumption is considered:

Assumption 1: rank[B]=rank[Bρ],∀ρ∈{ρ1,…,ρH}

Lemma1[13-14]Ifρsatisfies Assumption 1, then there is a positive scalarμ>0 such that

BρBT≥μBBT,

(9)

1.3 Fuzzy Logic Systems

A lemma in only given here owing to the page limit.

Hence, the unknown nonlinearitygi(x) can be approximated by

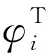
whereθi=[θi1,…,θil]T∈Rl,φi(x)=[φi1,…,φil]T∈Rlandεi(t)∈Ris a bounded function, i.e., ‖ε(t)‖≤ε.

Hence

where

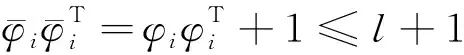
(10)

Based on FLS, the system can be rewritten as

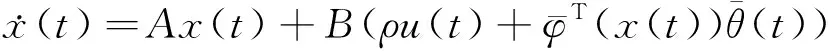
(11)

1.4 Control Objective

The goal is to develop a FLSs-based controller with fault-tolerant function such that the UAV system (11) is UUB.

2 Main Results

2.1 Controller Design

To compensate for the influence of actuator faults, the following fault-tolerant controller is developed:

u(t)=u1(t)+u2(t),

(12)

where

u1(t)=-k1(t)BTPx(t)

(13)

and

(14)

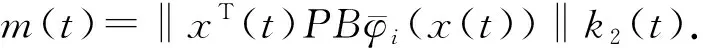
whereγ1andγ2are any positive constants.

2.2 Stability Analysis

Theorem 1: Consider the UMV system (4). If there is matrixP>0 such that

PA+ATP-2PBBTP+PEETP+γP<0

(17)

Then, by using the controller (12) with adaptive parametersk1(t) andk2(t) in (15) and (16), the boundedness of all the signals (includingk1(t) andk2(t)) in the closed-loop system can be achieved and the state of the UMV system (4) is UUB and belongs toD, where

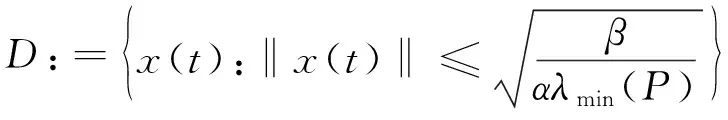
(18)

Proof. Consider the Lyapunov function

The derivative ofVis given by

By using Young’s inequality, we have

According to (13) and (15), one has

The following proof can be divided into two parts:

Fig.2 Trajectories of x(t)

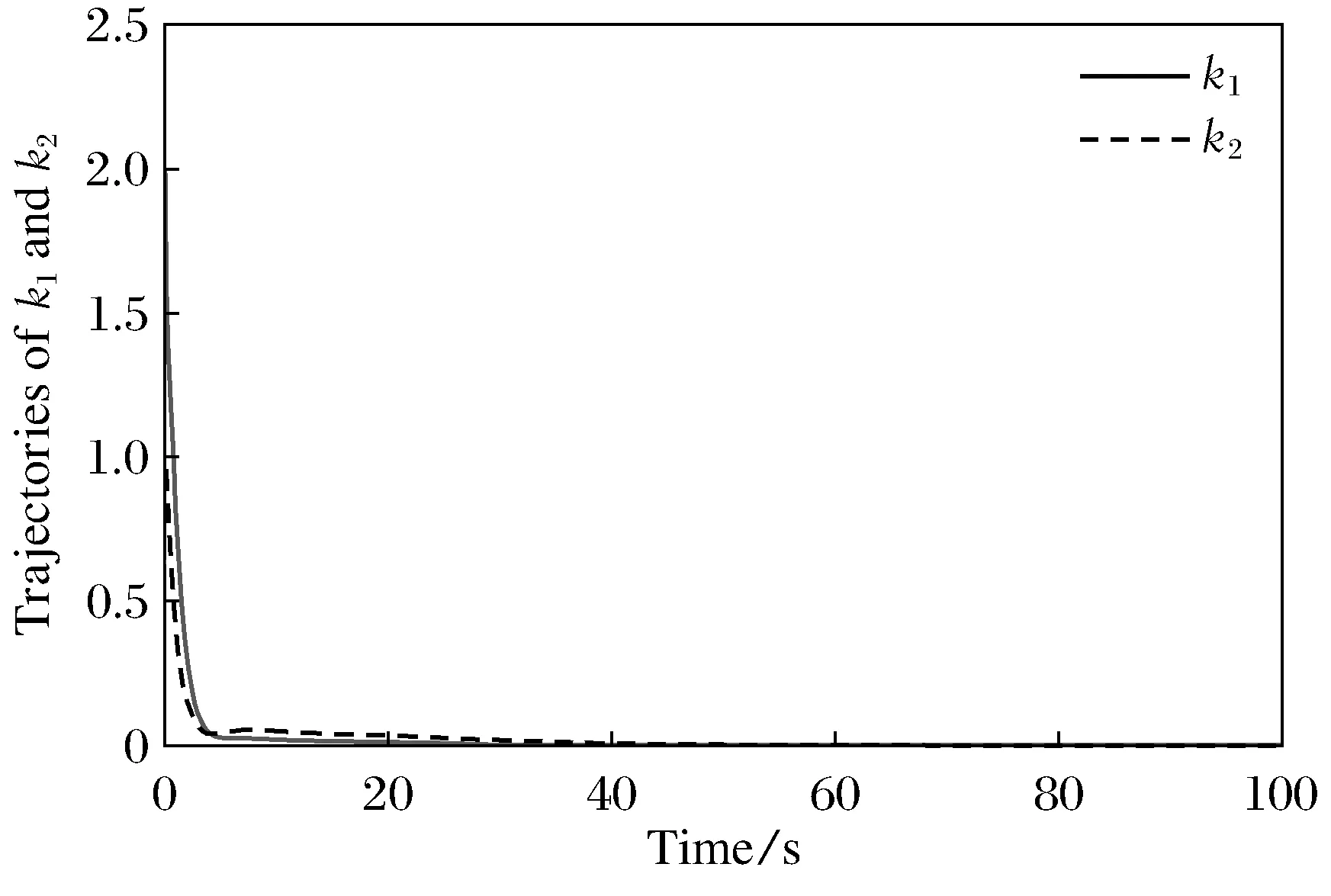
Fig.3 Trajectories of adaptive parameters k1(t) and k2(t)

According to (21)～(23), one has

(24)

Furthermore, one has

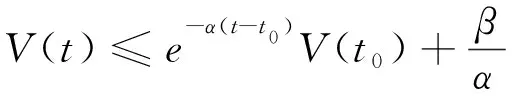
(25)

which shows that the boundedness of all the signals (includingk1(t) andk2(t)) in the closed-loop system can be achievedx(t) is UUB andx(t) converges to the setD. The proof is completed.

3 Simulation Results

Consider the UMV system (1) as described in [9], where

The initial states of the system arex(0)=[-10; 0; 10]Tandk1(0)=k2(0)=1. The trajectories of statex(t) and adaptive parametersk1(t) andk2(t) are respectively shown in Fig.2 and Fig.3, from which we can see that all the signals in the closed-loop system are bounded. This shows that the developed method is effective to solve the considered problem.

4 Conclusions

In this paper, the unmanned marine vehicle model has been established as a linear system with matched unknown nonlinear uncertainty. The nonlinearity has been approximated by using the FLS. By estimating the norm of the weight vector in the fuzzy logic system, the number of adaptive parameters has been reduced effectively. Furthermore, it has been proven that the asymptotic convergence can be achieved by the developed method. Finally, a simulation example has been used to demonstrate the efficiency and effectiveness of the developed approach.