分布式监测系统中的重复元素检测机制

陆 乐 孙玉娥 黄 河,3 汪润枝 曹 振

1(苏州大学计算机科学与技术学院 江苏苏州 215131)2(苏州大学轨道交通学院 江苏苏州 215137)3(中国科学技术大学苏州研究院 江苏苏州 215123)

近年来，随着分布式服务架构的流行，人们越来越关注分布式系统中各节点的数据整合问题.如何通过尽可能少的通信开销整合各分布式节点存储的数据，并从中提取出有用的信息来帮助系统做出更好的决策，已经成为人们研究的重点之一.给定一个阈值，当一个元素被不少于该阈值个节点监测到时，我们就称该元素为重复元素.本文将研究分布式系统中的重复元素检测问题，即分布式系统中同时被不少于给定阈值个节点监测到的重复元素集合，属于节点数据整合问题的一种.对重复元素的有效检测在实际生产中有很多重要的应用，举出一些应用实例：

1) 在一个包含了大量可以独立检测恶意入侵行为节点的分布式入侵监测系统[1-2]中，每个节点只检测自己监控的区域是否遭到了入侵并记录入侵的相关信息，如入侵类型、地址等能区分不同入侵的数据.通过网络，这些节点将入侵记录上传到中央节点，由中央节点找出并重点处理其中威胁度较高的大规模恶意入侵记录，即被大多数节点检测到的入侵数据.

2) 如谷歌一类的在线搜索公司在世界各地都有自己的服务器，假设它们会记录下各自地区近期内搜索频次较高的热门关键词并将其传给中央服务器，那么中央服务器就能整合这些搜索数据，找出其中大部分地区的人的共同兴趣或者关注点.比如在谷歌流感趋势预测[3]中，谷歌通过收集和整合各个地区人们跟流感相关的搜索关键词数据，可以近乎实时地预测流感是否爆发以及流感爆发的区域.

目前的相关研究主要集中在分布式系统中对频繁元素[4-8]和全局元素[9-14]的检测上.其中频繁元素即为在整个系统中出现频率最高的s个元素，在这一类问题的模型中，同一元素可以被一个节点记录多次.文献[4]针对频繁元素检测问题提出了一个多层次检测模型，将节点划分为多个层次，通过中间节点的数据整合减小最终传输给中央协调器的数据量，但该方案并不能有效降低整个过程中消耗的通信代价；文献[5]先让各节点找出本节点中出现频次最高的s个元素，然后将其发送给协调器以计算出一个更低的频次阈值并发回给各节点，然后节点再将出现频次超过该阈值的所有元素发给协调器，由其找出其中的频繁元素.然而，上述研究并不适应于重复元素检测.这是因为重复元素检测要计算每个元素被多少个不同节点监测到，而与该元素在每个节点上出现的次数无关.与本文研究问题类似的是全局元素检测，即找到被所有节点监测到的元素，是重复元素中的一个特例.文献[9]中提出一种基于任意2个节点记录的元素集合差异较小的假设的全局元素检测算法，但这一假设与实际不符，在节点差异较大的情况下其通信开销甚至超过了直接传输原数据的直观算法；文献[10]中提出的CFSP(combinable filter solution with progressive filtering)算法通过布隆过滤器[15]对节点数据进行压缩，并在协调器端将压缩数据通过逐位相与的方式整合后发回各节点以筛去节点中的无关元素，最终经过多轮筛选在给定的误差范围内找出系统中的全局元素集合.CFSP算法可以有效降低检测过程中的通信开销，但其在参数设置过程中并没有从全局最优的角度进行参数优化，所以在理论上并没有取得最佳效果.此外，全局元素本身也存在着很大的局限性.以分布式入侵监测系统为例，入侵者如果有意识地漏过1～2个节点不去攻击，就不会被全局元素检测算法检测到.因此本文在CFSP算法的基础上，提出了一个更为普适的问题模型，并给出了一个检测重复元素的有效解决方案。此外，本文还通过概率推导从全局最优的角度对参数进行了优化，并且增设了对筛选停止条件的判断，从而保证了每一轮筛选的收益最大化。

与本文最为相关的研究是文献[16]中提出的利用Cuckoo Filter和Raptor Code来检测重复元素的DISPERSE(probabilistic distributed persistent item identification algorithm)算法，但误报和漏报情况的存在使其难以适用于某些严苛的应用场景.

在重复元素的检测过程中存在4个难点：

1) 大规模的分布式系统会产生巨量的数据，这些数据的传输会给协调器和整个系统造成极大的压力，因此需要尽可能降低探测过程中的通信开销，避免原始数据的直接传输.

2) 系统中不同节点记录的数据量可能大致相仿，也可能差异巨大，机制针对不同的元素分布状况，都要能达到预期的效果.

3) 为了便于统筹全局，做出决策，协调器需要掌握所有重复元素的信息，而这些数据都是分散存储在各个节点中的.

4) 在某些应用场景下，重复元素的误报或漏报可能造成巨大的损失，为了适用于类似场景，机制要完整、无误报地检测出所有重复元素.

针对以上4个难点，本文以降低通信开销为目标，设计了一个适用于大规模分布式监测系统的重复元素检测机制，保证协调器可以完整、高效、无误报地完成重复元素的检测.

1 系统建模

本节给出了分布式监测系统的模型，并对所要解决的问题进行了具体阐述.

1.1 系统模型

如图1所示，所研究的分布式监测系统部署在网络中，主要由1个中央协调器和n个监测器组成.每个监测器独立地监测网络数据流中的元素，这里的元素可以根据实际的应用需求定义.例如，在扫描攻击检测应用中，每台监测器是一个服务器，而一个元素则是一个访问该服务器的源地址.由于本文只研究如何检测网络中的重复元素，并不需要考虑每个元素在同一监测器中出现的次数，所以假设同一监测器所保存的元素集合并不存在相同元素(即已经完成去重操作).

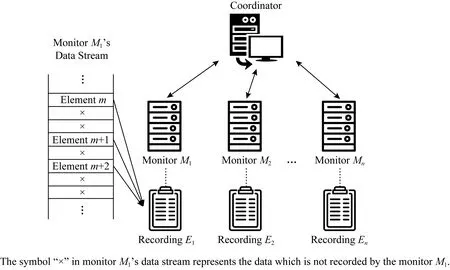
Fig. 1 The distributed monitoring system model图1 分布式监测系统的系统模型

当需要进行重复元素检测时，每个监测器Mi首先开辟一块大小为li的内存空间，用于存储所监测到的元素集合Ei.由于元素的数量可能非常庞大，直接发送原始数据会带来巨大的通信负担.为了节省传输带宽，本研究采用布隆过滤器存储元素，而每个监测器上布隆过滤器的大小li由所监测到的元素数量决定.然后，监测器将编码后的布隆过滤器发送给协调器.协调器在收到所有监测器发来的数据后会对其进行整合，然后通过与监测器之间的多轮通信、协作计算完成重复元素监测工作.

1.2 问题描述及设计目标

实际应用中，根据应用场景的不同，元素的定义可以非常宽泛.它可以是1个搜索频率极高的热门关键字、1条被蜜罐捕获的入侵记录或是1个被检测系统判定为攻击源的IP地址.在本文中，任意2条元素，只要内容相同，就会被认定是同一条元素.因此，1条元素可以出现在多个不同监测器的记录列表中.下面我们给出t-重复元素的定义，这也是本文研究的主题.

定义1.t-重复元素.在一个检测周期中，如果某条元素被n个监测器中的至少t个记录下来，那么称该条元素为t-重复元素.

本文研究的目标是通过监测器与协调器间的1轮或多轮通信，筛去各监测器列表上的非t-重复元素，使协调器能用尽可能少的通信资源，找到一个包含了本周期内系统中出现的所有t-重复元素的集合，此处记为Pt.参数t作为界定t-重复元素的阈值，其数值的改变会很大程度上影响Pt的内容.在t取不同数值的情况下，Pt可能包含大量甚至全部的元素，也可能仅仅是某个集合Ei的一个子集.

在寻找Pt的过程中，本文提出的机制需满足3点设计目标.

1) 完整性.在一些严格的应用场景下，系统必须保证协调器找出的解是没有遗漏的，即集合Pt要包含所有t-重复元素.

2) 无误报.最终解不能存在任何误报的情况，任何一个非t-重复元素都不应属于Pt.

3) 筛选的必要性.机制中进行的每一轮筛选操作都应该是必要的，即相对直接发送剩余元素原始数据的方案而言，本轮的筛选能够确实有效地降低整体的通信开销.

基于以上考虑，本文以最小化中央协调器与监测器之间的数据传输总量为优化目标，提出了一个高效的t-重复元素检测机制，在保证监测准确率的基础上，尽可能地降低对传输带宽的占用.

2 t-重复元素检测机制

本节给出了t-重复元素检测机制的设计细节，主要包括检测流程以及前2轮和后续轮次筛选过程中的参数优化，并对机制的性能进行了分析.

2.1 检测流程

对于t-重复元素检测问题而言，一种简单直观的做法就是令各监测器直接将元素列表全部发送给协调器，协调器经过比对后就能准确无误地找出所有t-重复元素.这种方法思路简单、易于操作，但会产生巨量的通信消耗，在大规模分布式监测系统中尤其如此.而要让协调器检测到存储在各个监测器端的所有t-重复元素，这些t-重复元素的直接传输又是必要的.因此，为了降低整体的通信成本，本机制的基本思路是通过监测器与协调器之间多轮的压缩数据交互，筛去监测器端元素列表中绝大部分的非t-重复元素，从而减小需要直接传输的元素的数量.

当一个监测周期结束时，系统即开始本周期的t-重复元素检测.由于布隆过滤器具有结构简单、空间复杂度低以及无漏报等优点，本文将其作为监测器压缩元素列表的工具.在用布隆过滤器对元素列表进行编码之前，监测器需要先用计算得到的布隆过滤器的参数，即位数组的大小l和Hash函数数量k，对其进行初始化.初始化完成后，各监测器首先将列表中的所有元素在对应的布隆过滤器上置位.

具体的置位流程为：对于每个元素，布隆过滤器通过给定的k个Hash函数将其随机映射到长为l的位数组上的k个位置，并将这些位的值置为1.置位完成后，监测器将各自的位数组发送给协调器，由协调器将接收到的所有位数组通过逐位累加的方法进行整合，把累加后数值大于等于t的位置为1，其余位则置0，从而得到一个整合了所有元素数据的结果位数组.此后这个结果位数组会被协调器发回给所有监测器，每个监测器对照着它用原来的k个Hash函数将自身列表中的元素一一映射到对应的k位，若这k位全部为1，那么这条元素可能是t-重复元素，监测器依旧将其保留.若这k位不全为1，基于布隆过滤器无漏报的特性，该元素一定是非t-重复元素，监测器会将其从列表中移除.当所有元素都在结果位数组上验证过一遍后，这轮筛选便到此结束.

系统重复上述步骤，进行下一轮的筛选，直到监测器接收到协调器的终止命令为止.筛选结束后，监测器将列表中剩余的所有元素直接发送给协调器，协调器通过对比找出所有t-重复元素.

在筛选阶段，使用布隆过滤器进行数据的编码压缩在判别时总会有一定的误报率存在，所以即使经过多轮次的筛选，机制也无法保证所有的非t-重复元素都已经被监测器筛去.但无论监测器最终传输的元素中是否包含非t-重复元素，机制都能确保协调器可以准确地找到Pt.因此筛选阶段允许误报的存在，且本文不关心误报率的大小，下一轮筛选对整体误报率的影响并不能直接决定筛选是否继续进行.后续筛选的必要性只取决于其是否能给系统整体带来收益，即通信开销的降低，而这一点将交由协调器判断.为了让协调器能够通过逐位累加的方法整合布隆过滤器，所有监测器对应的布隆过滤器理论上应该保持一样的大小l，并使用相同的k个Hash函数进行置位.

记第q轮筛选中监测器Mi对应的布隆过滤器为Bi,q，其对应的位数组长度为li,q，统一的Hash函数数量为kq.紧接着将介绍协调器怎样判断筛选何时停止以及如何给各布隆过滤器分配合适的参数，因为不同阶段元素集合的情况有所差异，本机制为前2轮筛选和后续筛选分别设计了不同的参数优化方案.

2.2 首轮筛选机制

Fig. 2 Convert the bloom filter to the extended one by replicating itself twice图2 通过2次自我复制扩展布隆过滤器

根据文献[15]提供的单个布隆过滤器最优参数的推导，监测器Mi可以计算得到对应布隆过滤器的最优参数，首先是位数组的理论大小li,1：

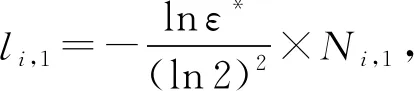
(1)

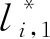
(2)

对于Hash函数个数k1，监测器同样依据文献[15]给出推导计算它的实际最优值：

(3)

由于ε*采用统一的预设值，所有监测器求得的k1也是一致的.

第1轮筛选会筛去大量的非t-重复元素，使得后续轮次的筛选中各监测器元素数量不均衡的状况得到大幅度的改善.所以在此后的第q轮筛选中，机制会以满足剩余元素数量最多的监测器Mmax,q的需求为标准，为各监测器设置统一的布隆过滤器大小lmax,q和Hash函数数量kq.因此lmax,q和kq需由协调器在掌握了所有监测器的具体情况后计算得到并分配给各个监测器.

2.3 首轮筛选后的参数优化

第2轮筛选开始前，各监测器会先将各自列表中剩余元素的数量Ni,2发送给协调器.协调器收到所有监测器信息后，会找出其中的最大值Nmax,2，然后以Nmax,2为基础为各监测器计算统一的lmax,2和k2.计算方式与第1轮筛选中类似：

(4)

此后协调器会将lmax,2和k2发送给各监测器，以供它们对布隆过滤器进行初始化.

一般情况下，前2轮筛选都能够大幅降低通信开销，所以不考虑其必要与否.而在后续的数轮筛选中，协调器就需要在筛选前判断该轮筛选的必要性以决定是否继续进行筛选了.

2.4 后续筛选的参数优化

相比于前2轮筛选，后续几轮的筛选从前次筛选中继承了各监测器对元素列表用布隆过滤器编码后产生的大小一致的位数组.借助这些数据，协调器可以在筛选开始前对元素的分布状况进行预估.记只出现在m个监测器列表中的元素数量为fm，在前次筛选整合出结果位数组前，协调器只要分别统计出逐位累加后各个位中数值等于0,1,…,n的位的数量，根据文献[17]中提出的持续流量估计算法，就能够以较高的准确率估计出fm的值.由于原算法是基于1次Hash置位的Bitmap进行的流量估计，而在本文中，输入是kq次Hash置位的位数组，所以在计算出数值后还要将其除以kq以得到对fm的估计值.

对于只出现在m个监测器列表中的元素被记录下的次数，可以用m×fm进行计算.根据t-重复元素的定义，协调器能够估计出t-重复元素在所有监测器列表中数量的总和：

(5)

根据布隆过滤器的相关理论，只要给定了待编码集合的大小以及期望的误报率阈值后，协调器就能依照公式计算出单个布隆过滤器的最优参数.但是单个布隆过滤器的最优并不等同于多个布隆过滤器整合后的全局最优，在本机制的筛选过程中需要考虑的是全局的筛选成本和效果.因此在具备估计不同出现次数的元素分布状况的条件后，本文给前2轮筛选外其他轮次的筛选设计了考虑全局最优的参数优化方案.

在第q轮筛选中，协调器在已知各监测器拥有的剩余元素数量的情况下，不仅要为所有布隆过滤器统一分配一个合理的lmax,q和kq，还要判断该轮筛选是否有必要进行.为此，本文为第q轮筛选构造了一个收益函数pq：

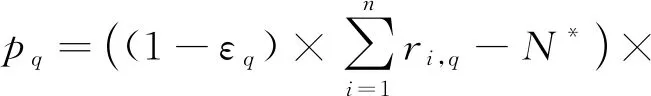
(6)

在定义了第q轮筛选的收益后，本轮的优化目标自然是将收益最大化.由于最大化pq隐含了用尽可能少的通信开销筛去尽量多的非t-重复元素，因此在优化过程中不必要对筛选的效果做额外的约束，可以将第q轮筛选的优化方程规约为

maxpq
s.t. 1≤kq≤lmax,q,

(7)

其中，εq表示第q轮筛选的理论误报率.文献[17]中有类似的推导过程，只需要将由置位1次的Bitmap扩展到置位k次的布隆过滤器即可，此处直接给出推导结果：

(8)

其中，Pi可令i从0取到n依次计算得到：

(9)

将式(6)(8)(9)代入式(7)中，求解优化问题，协调器可以得到kq和lmax,q的值，同时也能够解出本轮收益pq.在第q轮筛选的参数优化中，文献[17]提出的持续流量估计算法的时间复杂度与空间复杂度为O(N)，N为第q轮筛选前系统中的元素总数.求解优化问题则需要遍历每一对可能的(lmax,q,kq)组合并计算对应的收益pq以找出最优解，其时间复杂度为O(Lmax,q×Kmax,q)，空间复杂度为O(1)，其中Lmax,q和Kmax,q分别表示第q轮筛选中lmax,q和kq可能的最大值.综上，第q轮筛选的参数优化算法的时间复杂度为O(N+Lmax,q×Kmax,q)，空间复杂度为O(N).

根据pq的定义，当pq≤0时，本轮筛选无法给整个探测过程带来任何收益，甚至会提高总体的通信开销.此时将参数发送给监测器，继续第q轮的筛选显然是不合适的，协调器将依据pq的值决定筛选是否继续.筛选过程会耗费一定的时间成本，所以当收益不大的时候，筛选带来的通信开销的降低可能不足以弥补其所消耗的时间.因此，可以根据具体应用场景的要求和系统的规模为收益设置一个阈值λ，当收益≤λ时，则认为没有继续下一轮筛选的必要.

(10)

算法1.第q轮参数优化算法(q≥3).

输入：各监测器持有元素数目集合{Ni,q}i∈[1,n]、估计的t-重复元素数目N*、收益阈值λ；

输出：统一的布隆过滤器的大小lmax,q、Hash函数数量kq或终止筛选的信号.

① 据文献[17]的算法估计{f1,f2,…,fn}；

② 据式(5)估计N*并更新；

③ 据式(6)(8)确定pq，εq；

④ 据式(7)解出lmax,q，kq并计算pq；

⑦ returnlmax,q，kq；

⑧ else

⑨ return终止信号；

⑩ end if

2.5 机制分析

本文提出的t-重复元素检测机制最重要的目标是用尽可能少的通信开销完整、无误报地找出单个监测周期中系统内所有的t-重复元素.基于这一目的，上文为t-重复元素检测问题制定了3个设计需求，接下来将证明本机制是满足这3点需求的.

定理1.所设计的t-重复元素检测机制可以保证探测结果的完整性.

监测器主要依靠布隆过滤器进行数据压缩.在任意的第q轮筛选中，根据布隆过滤器的运作原理，任意一条t-重复元素在其被记录的至少t个监测器的布隆过滤器上都会被映射到相同的kq位，且这些位置都将被置1.因此数据整合后其对应在结果位数组上的kq位也将全部被置为1，当这些记录了它的监测器查验自身元素列表时，该条元素会被保留.所以筛选过程中可以确保不会剔除任何一条t-重复元素.而最终协调器整合元素数据的过程中，对于这些被至少t个监测器传输来的元素，协调器不会有任何检测缺漏的情况，即机制可以完整地检测出所有t-重复元素.

定理2.所设计的t-重复元素检测机制可以保证探测结果的无误报.

对于监测器元素列表中存在的非t-重复元素，虽然多轮次的筛选无法保证将其全部筛去，但可以证明它们并不会影响探测结果的准确性.在最后协调器的整合步骤中，各监测器将包含了少量非t-重复元素和全部t-重复元素的元素集合传输给协调器.通过比对所有接收到的元素集合，协调器可以找到所有的t-重复元素.而对于非t-重复元素，以监测器Mi中的某条非t-重复元素为例，当且仅当其本就在监测器Mi的列表中且通过了多次筛选，它才会最终被发送给协调器.假设它被协调器误报为t-重复元素，则它必须出现在至少t个监测器的传输列表中，即它在本周期内确实地被t个或更多的监测器记录了下来，那么按照定义，它应当是一条t-重复元素，因此假设并不成立，本文提出的机制可以满足探测结果无误报的要求.

定理3.所设计的t-重复元素检测机制可以保证每一轮筛选的必要性，从而最大程度降低通信成本.

在满足了结果准确性需求的前提下，机制的性能也需要得到保证.本文给出的机制综合了t的取值以及所有监测器拥有元素的数目等因素从全局最优的角度对各监测器对应的布隆过滤器进行了参数优化，因此无论元素在各监测器列表中的分布状况如何，机制都能保持良好的性能.而筛选终止条件的判断则确保了每一轮筛选都是能够取得收益的必要筛选，使得通信开销永远随着筛选轮次数的递增而递减，因此可以最大程度地降低通信成本.

3 实验分析

本节给出仿真实验的具体细节，结合对比实验分析了机制在降低通信开销上的效果，并验证了机制在不同元素分布状况下的性能.

3.1 实验设置

本文实验采用了公开数据集CAIDA中的真实网络流量数据作为数据集，取其中12 min内服务器记录下的IP访问信息，将其划分为12个时间片.实验中，每个时间片(1 min)的数据都会被模拟为分布式监测系统中一个监测器节点所记录的元素列表.在模拟的系统中一共有4 100 541条元素.其中每条元素包含1个源地址和1个目的地址，大部分IP地址都是IPv4地址，只有极少量的IPv6地址，所以直接发送1条元素的通信开销h在本次实验中被设置为64 b.在系统包含的12个监测器节点中，元素的分布大致均匀，平均每个监测器约有34万条元素记录.为了适应各种应用场景，本文将t-重复元素的阈值t的数值设为4～12之间的任意数值，设收益阈值λ=0并分别进行实验，实验结果均为多次实验后得到的平均结果.

本次实验的实验环境为Intel®CoreTMi7-7700 CPU 3.60 GHz，16 GB RAM.

3.2 性能分析

为了用作对比实验，本文将文献[10]中提出的CFSP算法加以修改，在整合压缩数据时用逐位累加的方法取代逐位与，并在筛选结束后将剩余元素全部发送给协调器，以适应所要解决的t-重复元素检测问题.此外，虽然DISPERSE算法存在误报与漏报情况，本文同样将其与直观算法一起纳入对比.实验将从通信开销、时间开销、误报漏报、算法的鲁棒性等方面对机制进行评价.

4种算法的通信开销如图3所示，随着阈值t的增大，改进后的CFSP算法和本文提出的机制所耗费的通信开销不断降低，DISPERSE算法的通信开销基本趋于稳定，直观算法的通信开销则始终保持在一个定值.这是因为，t值的增大意味着t-重复元素的减少，所以在筛选过程中可以筛去更多的无关元素，进一步降低了整体的通信开销.而无论t取何值，DISPERSE算法都需对所有元素进行编码并且只依赖1次通信获取结果，因此开销趋于稳定.直观算法中监测器总是将所有记录下的元素直接发送给协调器，其通信开销也是固定的，与t的取值无关.可以看到，无论t取何值，所提出的机制总能在通信开销的降低上取得较高的收益.当t>8时，机制的收益优于其他3种算法.根据t的不同取值，本机制相比于直观算法可以降低14%～79%的通信开销，相比于改进后的CFSP算法可以降低8%～26%的通信开销，t>8时与DISPERSE算法比较可以节省11%～42%的通信开销.机制会持续3～4轮的筛选，相较于改进后的CFSP算法节省了3～4个轮次.

Fig. 3 Communication cost of our scheme andother three algorithms using the original data图3 原始数据下机制与3种算法的通信开销对比

因为DISPERSE算法的特殊性，表1单独列出了其与本机制的性能数据以作对比，包含了全局的通信开销、误报率和漏报率.表1中的FPR(false positive rate)代表检测结果中被误判为t-重复元素的非t-重复元素在所有非t-重复元素中所占的比例，即误报率.而FNR(false negative rate)代表未被检测出的t-重复元素在所有t-重复元素中所占的比例，即漏报率.从表1可以看出，随着t值的不断增大，2种算法的通信开销都呈下降趋势.但相比之下，本机制的通信开销下降速度更快，在t=8时基本与DISPERSE算法持平，此后的通信开销更是优于DISPERSE算法.此外，本机制在实验中始终没有出现误报漏报现象，而DISPERSE算法在保持着极低的误报率的情况下，其漏报率却不容忽视，且漏报率会随着t值的增大而增大，从14%～38%不等.因此，相比于DISPERSE算法，本机制具有更为优越的性能.

由于实验使用了连续时间片的网络流量数据对监测器的元素记录进行模拟，元素在系统中分布得较为均匀.为了检测机制的鲁棒性，我们进一步地对数据进行一定的处理，为每一个时间片随机初始化一个概率并依据该概率在该时间片数据中随机选取一些数据丢弃.经过处理后，每个时间片包含的数据量从2～27万条不等，由此模拟出的分布式监测系统中，元素在各监测器中的分布状况极不均衡.在此基础上，实验结果如图4所示，可以看到，即使在元素分布不均匀的状况下，本机制依旧可以保持良好的性能，甚至比在元素分布均匀的系统中表现得更为优越.而当t的取值较小时，CFSP算法则表现得有些不稳定，t=4时其消耗的通信成本甚至超过了直观算法.机制相较直观算法可以节省28%～96%的通信开销，相较改进后的CFSP算法可以节省21%～47%的通信开销，t>4时与DISPERSE算法比较可以节省9%～91%的通信开销.

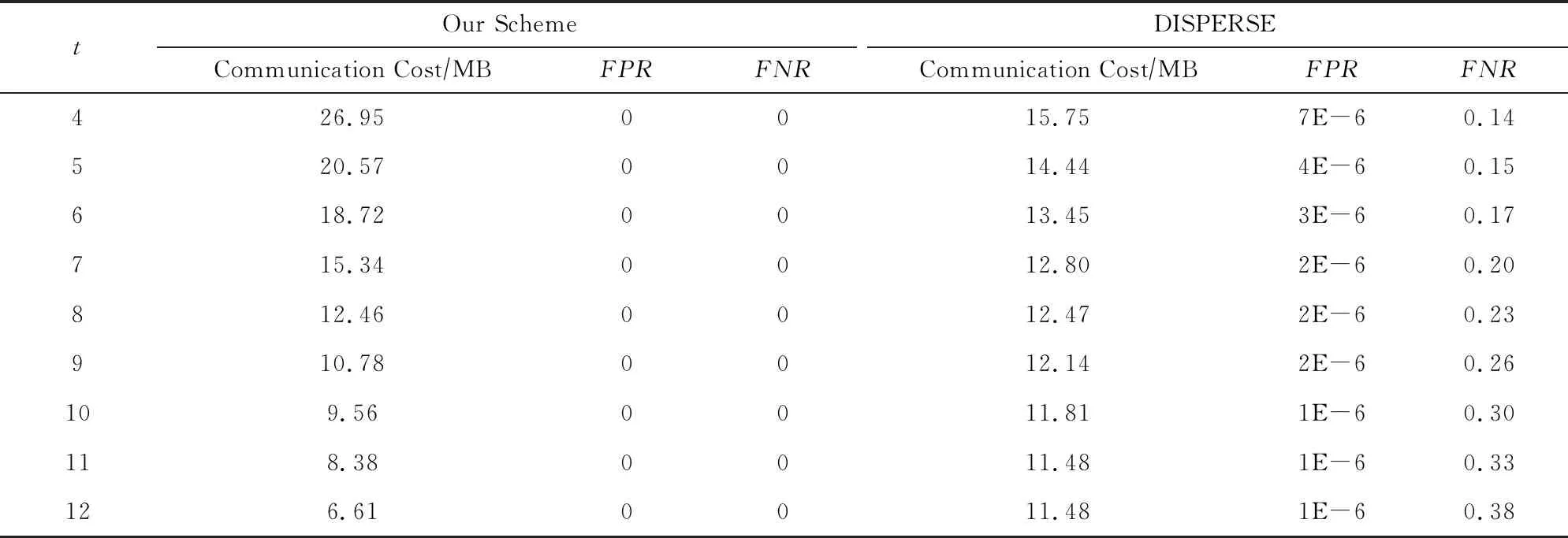
Table 1 The Performance Comparison of Our Scheme and DISPERSE Using the Original Data

Fig. 4 Communication cost of our scheme and other three algorithms using the processed data图4 处理后数据下机制与3种算法的通信开销对比

在实验中，根据t的不同取值，筛选会持续3～4个轮次.其中当t=8时各轮筛选的表现情况如表2所示，系统总共进行了3轮筛选即达到终止条件，在此基础上又额外进行了第4轮筛选以作比较.

从表2可以看出，随着筛选轮次的增加，筛选的收益在不断减小.这是因为筛选降低的通信开销和该轮筛选滤去的元素数量呈正相关，和每条元素的平均过滤代价呈负相关.伴随着筛选的进行，非t-重复元素的数量大幅度减少，筛选中可以滤去的元素数也随之减小.而压缩过程中用于给t-重复元素编码的那部分数据大小基本稳定，且在筛选耗费的总成本中的占比不断增加，这使得筛选成本的降低幅度远远比不上筛去元素的减少幅度.因此随着筛选次数的增加，筛选的收益，即其降低的整体通信开销不断减小.到了第4轮筛选，一共只筛去了48 635条元素，平均筛去1条元素需要108.5 b，而直接传输1条元素仅需64 b，所以该轮筛选反而让整体收益有所降低.

Table 2 Performance of Each Round Using the Processed Data when t=8表2 当t=8时处理后数据下各轮筛选的表现情况

此外，实验还从时间开销的角度对机制进行了性能分析.本机制的时间开销主要可分为通信和运算2部分.其中通信时间与通信开销成正比，比如在100 Mbps的网络环境下，无论t取何值，机制都能在1～2 s内完成所有的数据传输.即使在50 Mbps的网络带宽下，机制也能在3 s内完成通信.接下来主要对运算时间进行分析，其结果如表2所示.依照机制的检测流程，本文将一轮筛选的运算时间划分为监测器端和协调器端2部分，协调器端的运算时间主要用于参数优化和整合位数组，监测器端的运算时间则包含了元素置位和筛去非t-重复元素所耗费的时间.其中，前2轮筛选的参数优化只进行了简单的计算，所以几乎不占用时间资源.而监测器进行置位和筛选是所有监测器同步进行的，所以只取这些监测器中运算时间的最大值.可以看到，随着筛选轮次的增加，元素列表的规模不断减小，监测器端所消耗的运算时间也呈下降趋势.在第3轮及后续轮次的筛选中，因为需要综合全局状况求解最优参数，所以相比前2轮筛选依据公式计算参数，协调器端需要更多的运算时间.

上述实验过程中，协调器总是依据对下一轮收益pq的预测未达到预期而发出终止信号，每一轮筛选都能有效降低整体的通信开销.而协调器给出的检测结果包含了所有t-重复元素，且没有任何一条非t-重复元素被误报，这也验证了此前的理论分析.

4 总 结

针对分布式系统中t-重复元素检测问题，以最大化降低通信开销为优化目标，提出了一种适用于分布式监测系统的t-重复元素检测机制.通过筛选过程中对监测器信息的整合和动态预测，确保了机制的强健性，保证了每一轮筛选通信代价的最小化.使用真实网络流量数据进行的模拟实验结果表明：无论系统中元素分布均匀与否，机制都能取得良好的效果.在相似的性能及实验环境下，机制的稳定性和在降低通信开销上的表现优于直观算法，改进后的CFSP算法和DISPERSE算法.