基于核密度估计的泥土物证分类方法
王 黎, 杨瑞琴*, 郭洪玲
(1.中国人民公安大学刑事科学技术学院,北京 100038;2.公安部物证鉴定中心,北京 100038)
泥土物证是一种常见的微量物证,常附着于现场不同物体以及嫌疑人身上。泥土检验的目的是提取泥土物证中包含的各类理化信息并由此将嫌疑人与案件及案件现场关联。对泥土物证的检验方法已较为完善,如颜色、粒径、有机物,元素(包括常量元素、微量元素)、微生物、植物、孢粉等[1]。如果能够对泥土物证这种复杂体系进行刻画,将会在案件侦破与庭审阶段提供强有力的支持。
元素分析是目前中国泥土物证分析中最常用的分析方法[2],该方法选取特定元素进行元素含量的测定,依次比较各种元素含量是否有显著差异。城市泥土样本元素含量分布是城市样本间比对的基础,前人的研究主要集中泥土元素含量的基础上,对于该物证的比对问题只能给出经验性的判断,缺乏相似度计算的数理统计方法,即没有建立泥土物证比对的标准[3-4]。
为给出泥土物证间的相似度大小,引入了核密度估计与似然比检验。在进行泥土元素检验时需要对该元素的样本分布进行估计,通常采用正态分布来拟合。但实验数据表明,仅有部分地区或者部分元素的数据结果符合正态分布,这时一些基于正态分布的假设检验方法将不再适用。首先针对这一问题引入核密度估计,对泥土元素数据的分布统一进行估计,选用高斯核函数并确定最佳窗宽,得到元素分布的概率密度函数。其次利用判别分析对泥土物证进行分类。判别分析在法庭科学领域的应用已较为成熟[5-6],但判别分析需要样本满足正态分布,因此引入核密度估计-似然比检验的方法可以在估算样本总体分布的基础上计算样本间的相似度,通过LR(likelihood ratio)的大小判断给出两样本相似假设的支持力度。
1 实验方法
1.1 泥土样本采集
在城市各个区县选取采样点。在选取采样点时,避开渣土,建筑垃圾,道路等受外来土或其他流动因素干扰较大的区域。在每个采样点以五点取样法,在每个点位铲去表层土、植被、腐殖质等,在2~3 cm深取约500 g土样,将五份样本混合均匀后装袋封存并标号。
1.2 样品前处理
烘干:将采集到的每一份样本装满培养皿(湿重约200 g),放在烘干箱以105 ℃条件烘干120 min。烘干后的样本需用纸质袋(纸质物证袋)封存,并将其置于干燥箱或者有干燥剂(无水硅胶)的干燥皿中保存且尽快进行后续处理。
研磨:先用20目分样筛将碎石、植物残渣、动物尸体(蚯蚓、昆虫等)等筛除。初筛样本采用球磨仪研磨,取烘干后的样本约50 g置于经酒精棉洗净的玛瑙桶中,并加入约20颗直径8 mm的玛瑙球,反复试验后将研磨程序设置为15 min,450 r/min。研磨后要确保样品全部通过200目分样筛。
1.3 样品制备与仪器分析
实验采用X射线荧光法在胶圈模具(内径3 cm)内装入足量已研磨泥土样本,置于压片机在20 MPa压强下压片3 min,将其制成厚约2 mm的薄片,放入X射线荧光仪(ZSX100e)分析[7],采用XRF内标法,以X元素为内标,测定Al、Si、Fe、K、Na、Mg、Ca、P、Mn、Ti相对百分含量。
2 数据分析
2.1 统计方法原理与方法
2.1.1 KS(Kolmogorov-Smirnov)检验
KS检验,基于累积频率分布,用于检验该样本分布是否符合某种理论分布。它假设两者无显著性差异,利用样本累积频率分布与理论分布的偏离值,来检验样本分布与理论分布是否匹配。当KS统计量显著性水平大于临界值P=0.05时,认为该样本符合理论分布。采用KS检验泥土样本元素含量是否符合正态分布。
2.1.2 核密度估计与最佳窗宽
核密度估计(kernel density estimation,KDE)是一种估计样本总体概率密度函数的非参数估计方法,在运用核密度方法估计元素分布的概率密度函数时,重点在于核函数K(x)的选取和窗宽h的确定。常用核函数有均匀核、三角核、二次核、四次核、高斯核、余弦核,采用高斯核函数。在窗宽的选择过程中指标积分均方误差(mean integrated squared error,MISE),MISE是核密度估计中常用的评价标准,其计算公式为
(1)
(2)
(3)
式(3)中:E为求期望运算。其中f(x)2不受核函数K(x)选择的影响,则可以定义代价函数Cn(h):
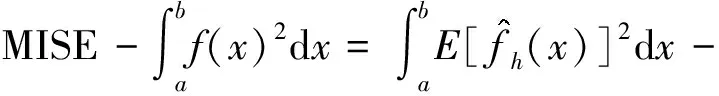
(4)

(5)
其中,ψh(ti,tj)为与样本ti,tj有关的积分变量,公式为

(6)
可以利用式(6)编程计算最佳窗宽值。
2.1.3 判别分析
判别分析是一种在一些已知研究对象用某种方法已经分成若干类的情况下,确定新的样品的观测数据属于哪一类的统计分析方法。常见的有距离判别、Fisher判别(又称线性判别分析,linear discriminant analysis,LDA)和贝叶斯判别。在法庭科学领域是常用的分类分析手段。采用Fisher判别法对实验数据进行分类分析。
2.1.4 似然比检验
似然比检验是一种反映样本灵敏度与稀有度的复合指标,是贝叶斯分析的一种特殊情况。在微量物证领域似然比检验的应用就是以零假设与备择假设之比的大小来衡量物证的价值,即实验结果E的条件下假设H1:源于同一客体的概率P(E|H1)与假设H2:源自不同客体的概率P(E|H2)大小的比值,即:
LR=P(E|H1)/P(E|H2)
(7)
为了让LR更直观地为调查人员接受,Evett等[14]提出了一种LR的习惯性表述(表1)。

表1 LR所代表的含义Table 1 The implication of the LR
采用Zadora等[15]提出的LR计算方法,在对h取值改进的基础上计算LR,从而对样本间相似度大小进行度量。
2.2 数据正态性检验
实验结果为福州(N=50)与呼和浩特(N=50)两地十种元素相对百分含量数据,由于各元素区间差异较大,因而统一对数据做对数变换。将转换后的数据进行KS正态性检验(IBM SPSS Statistics 20),检验结果如表2所示。结果表明只有少部分元素含量分布符合正态分布(Sig>0.05),因此采用核密度估计统一对元素含量分布进行估计,其中Mn元素数据波动极小(标准差σ=0.045 465,变异系数CV=-2.772%),拟合已无意义,不纳入后续数据处理过程。
2.3 最佳窗宽算法实现


表2 福州、呼和浩特泥土元素含量正态性检验结果Table 2 Results of normality test of soil elements in Fuzhou and Hohhot
注:*表示真实显著水平的下限;a表示Lilliefors 显著水平修正。
(2)编辑函数:
function(c)=Cn(h,t)
(8)
(3)调用(2)中函数,由小到大代入h,找到使得函数值最小的h,同时可做出函数Cn(h,t) 随窗宽h变化的趋势图(图1)。
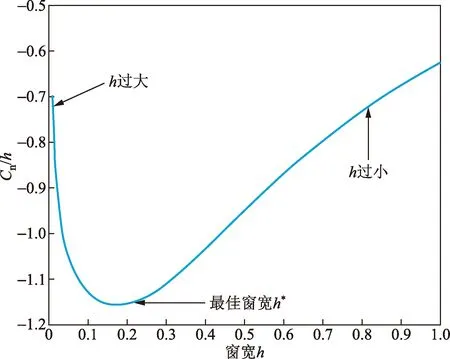
图1 窗宽h的代价函数(以福州市P元素为例)Fig.1 The cost function of the bandwidth h (take the Fuzhou P element as an example)

图2 福州市P元素最佳窗宽示意Fig.2 The best bandwidth for Fuzhou P element
以福州市P元素数据为例。经上述算法可得h*=0.017[Cn(h)min=-1.155],并按h*做出P元素概率密度函数(Rversion 3.5.2)。在图2中,在大于最佳窗宽h*处作图存在过拟合的情况,而在小于最佳窗宽处密度函数平滑性较差,图2(c)得到了最小代价函数条件下福州市泥土样本P元素含量分布。事实上,可以对所有元素样本总体分布统一采用KDE过程进行概率密度函数估计,便于后续分析,如表3所示。采用计算出的最佳窗宽可以得到元素分布的概率密度函数。得到的元素分布概率密度函数可以代入元素分类与比对的似然比模型,计算出样本间似然比值的大小作为分类与比对的依据。

表3 两地元素分布最佳窗宽Table 3 The best bandwidth of the element distribution between the two places
2.4 样本分类
2.4.1 判别分析
对福州市和呼和浩特市两地泥土样本进行费歇尔判别分析(IBM SPSS Statistics 20),如图3所示,判别结果表明两地泥土样本在市级层面有着良好的分类效果,数据总体分为了福州市与呼和浩特市两类,但在对市区间样本分类时效果不理想,判别率与回判率也较低(回判率63%,交叉验证正确率42%)。为对市区间样本进行合理分类,采用似然比检验计算样本间相似度大小。

图3 福州市与呼和浩特市泥土样本判别分析散点图Fig.3 Scatter plot of the discriminant analysis of soil samples in Fuzhou and Hohhot
2.4.2 似然比检验
将核密度估计得到的最佳窗宽h*取均值(h*=0.058 89) 后代入似然比检验,计算各市区样本间的LR,结果如表4所示。可以看到在市级层面比较,LR极小(表4左下部分),可以近似为0,即两市样本间存在较大差异。在区级层面比较,LR值大小不一(表4左上与右下部分),仓山区与台江区间LR(LR=3 704)较大,即对两区域样本相似的假设有着强烈支持;而回民区与赛罕区2号间的LR(LR=0.000 041 04)较小,即两区域样本差异较大。由此,表2所示矩阵可以清晰地给出区域间样本相似度的大小,直观判断两区域泥土样本是否相似,可作为判别分析的补充。
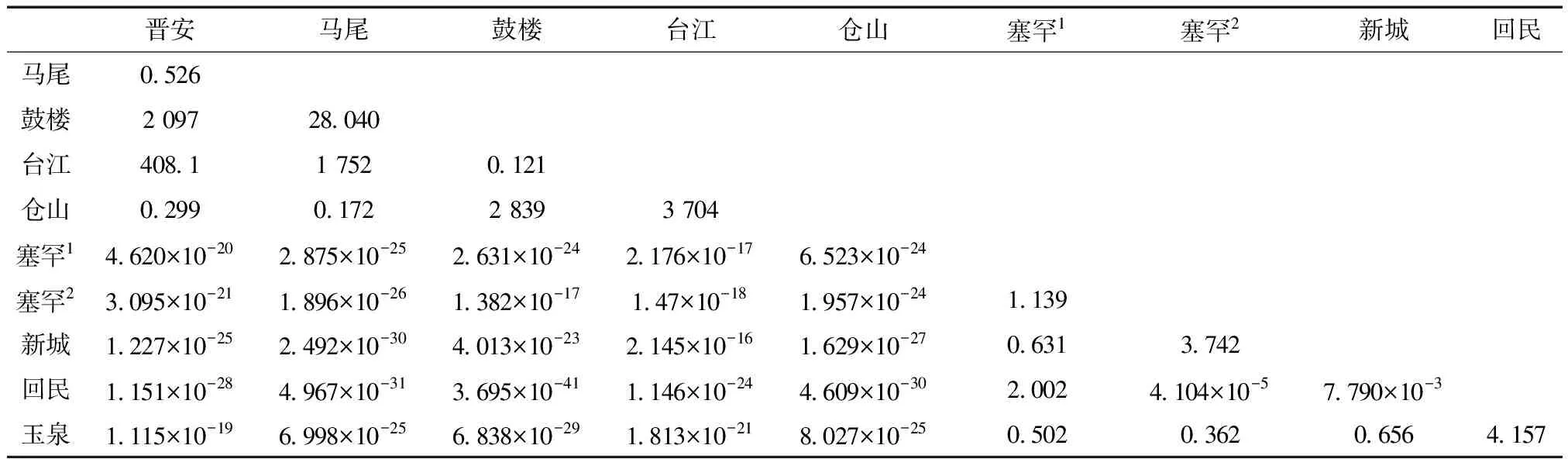
表4 福州、呼和浩特泥土样本区域间LRTable 4 LR between the soil samples of Fuzhou and Hohhot
注:上标1、2表示20个样本分别在呼和浩特市赛罕区的两个区域采集。
3 结论
在核密度估计过程中采用最小MISE准则,使拟合出的概率密度函数尽可能接近原始样本总体,是估计未知样本分布的可靠的方法。研究结果为不符合正态分布的样本总体提供了建立数据模型的手段,为泥土样本元素含量数据的概率密度函数估计建立了统一的方法。同时,针对不同层级的分类需求,初步利用判别分析与似然比检验建立泥土样本分类的方法。

