基于自回归模型和核主成分分析的结构损伤识别方法

郑泓，段忠东，王贞，李宏伟

（1.哈尔滨工业大学(深圳) 土木与环境工程学院；2. 宁波杉工智能安全科技股份有限公司）

近三十年来，结构损伤识别受到国内外学者的广泛关注和深入研究，特别是基于结构振动的损伤识别方法已取得一系列的研究成果[1]。其中，Farrar[2]提出的基于统计模式识别的损伤识别方法，直接对结构的响应数据建立时间序列模型，利用模型较少的参数进行损伤诊断，被认为具有较好的应用前景。

但是不管何种方法，环境因素（温度[3]、边界条件[4]、车辆荷载[5]、风速[6,7]等）的影响都有可能掩盖结构损伤导致的特征参数改变，使结构损伤识别失效。如何剔除或减少环境因素的影响，得到结构本身的真实状况，成为结构损伤识别方法实际应用中一个急需解决的 问题。

本文在考虑损伤和环境因素都会引起结构特征参数改变的前提下，提出了自回归模型（Auto regression-AR）结合主成分分析（Principal component analysis-PCA）、核主成分分析（Kernel Principal component analysis-KPCA）的损伤识别方法。通过工程实例表明该方法能有效消除温度对损伤诊断的影响。

1 基于自回归模型的损伤识别方法

1.1 自回归模型

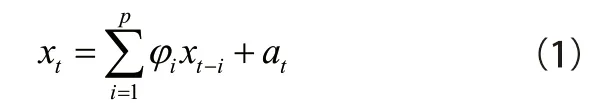
1.2 数据预处理

由于结构在环境激励下的响应信号并不一定满足平稳性和零均值，因此建模前必须对采集到的数据进行预处理，一般包括消除趋势项和标准化处理。本文采用基于EMD 的趋势项消除方法[8]和数据中心化方法[9]。

1.3 模型定阶

模型的阶次偏小会导致模型不能充分反映时间序列的统计特性；模型阶次偏大，不仅会降低参数估计的计算速度，而且由于参数估计方法自身存在计算误差，后续的损伤识别精度也会受到影响。对于自回归模型，模型阶次普遍采用由日本学者赤池（Akaike）提出的AIC 准则[10]。

1.4 参数识别

选取既满足模型精度要求又不影响计算效率的参数估计方法是建立自回归模型的另一关键问题。本文采用MATLAB 自带arburg 函数实现burg 算法[11]的自回归模型参数估计。

1.5 损伤特征提取

自回归系数反映了系统的固有特性，比较结构损伤前后这些参数的变化可以实现损伤识别。本文利用欧氏距离判别法定义损伤指标，其原理是利用结构完好状态（参考状态）和未知状态（待检测状态）的加速度时间序列建立自回归模型（参考模型和待检测模型），以两种模型自回归系数的欧氏距离作为损伤指标，设定合适的损伤阀值。当损伤指标大于损伤阀值时表明该结构状态改变（发生损伤），反之，该结构状态未改变（未发生损伤）。

2 主成分分析的环境因素消除方法

自回归系数的改变包含了损伤分量和环境分量，环境分量的存在会干扰损伤识别，甚至会产生错误的判定结果，消除环境分量能提高损伤识别准确度。

2.1 主成分分析的基本思想

在实际问题的研究中，为了全面揭示事物的本质规律，往往需要考虑众多变量。在保证这些变量所含信息丢失最少的前提下，主成分分析能用少数新变量代替它们[12]。

以AR(p)模型为例，n 个样本的自回归系数构成的矩阵为

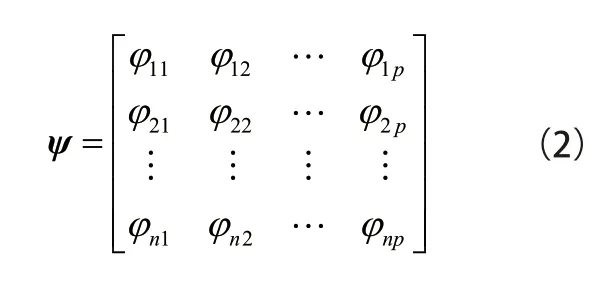
主成分分析就是将p 个观测变量经线性变换组合成p 个新的变量，即

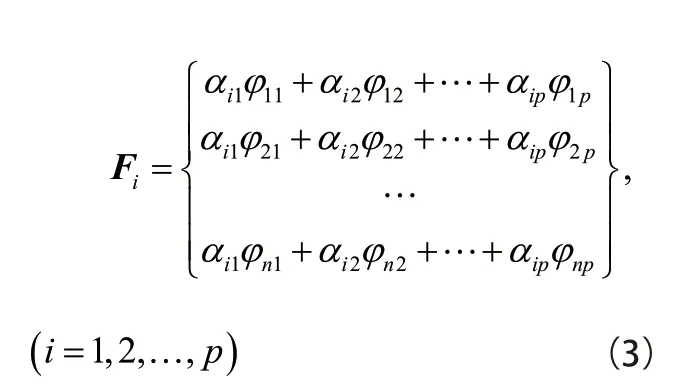
2.2 主成分分析的具体步骤

（1）数据样本标准化，令

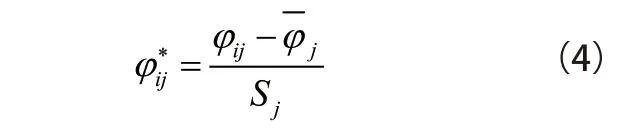
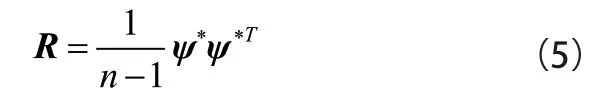
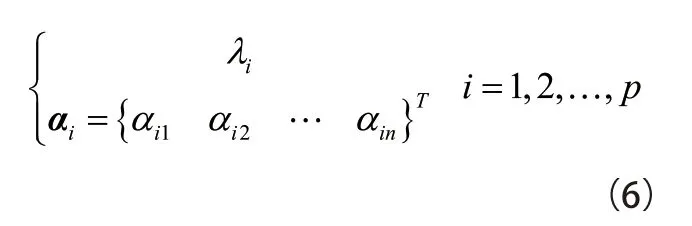
（4）根据式（3）求出各主成分值。

2.3 消除自回归系数中的环境分量

由2.1 节式（3）可得

假设存在某一环境因素的影响，n个样本之间必然存在差异，且该差异只与环境因素有关。由于第一主成分表征方差最大的分量，则该环境因素最有可能出现在第一主成分上。令第一主成分等于零，又根据A 为正交阵，可以得到消除环境影响的自回归系数为

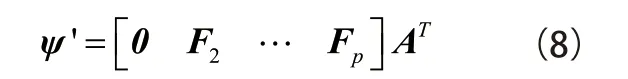
3 核主成分分析的环境因素提取方法

根据2.2、2.3 节，我们可以认为第一主成分的方差贡献率应该接近100%。第一主成分的方差贡献率越接近100%，环境因素的影响越显著。这里引入核主成分分析方法，相较于主成分分析，其优势是可以改变第一主成分方差贡献率的大小。

3.1 核主成分分析的基本思想

核主成分分析引入核方法的思想，构造核函数将低维的样本空间映射到高维的特征空间，在该特征空间进行主成分分析，求得各主成分。核函数[13]必须满足Mercer 条件，常用的有

（1）多项式核函数

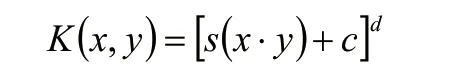
如果令式中的参数 0c= 、 1d = ，则多项式核函数退化成线性核函数，核主成分分析变为主成分分析。

（2）高斯核函数

仍以AR(p)模型为例，第i 个样本的自回归系数向量为

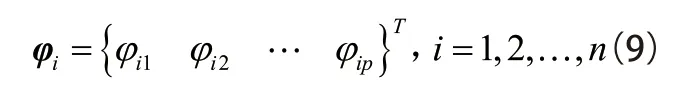
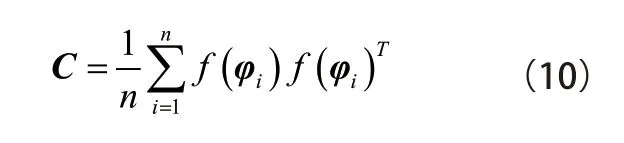
其特征方程为

式中λ和v 分别表示特征值和对应的特征向量。

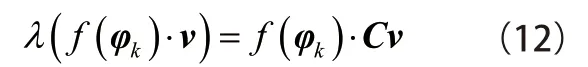
那么式（12）可改写为

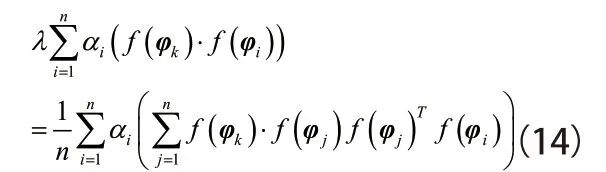
定义矩阵K为

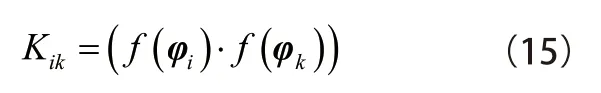
式（14）可简化为

通过求解式（16）可以得到n 个特征值-特征向量对

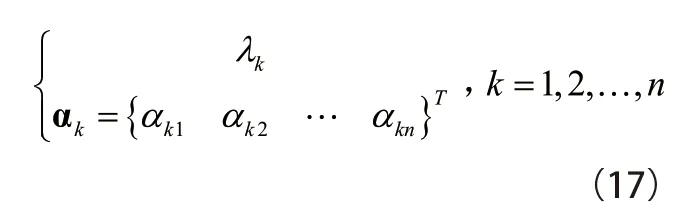
根据式（13）第k 核主成分对应的特征向量为

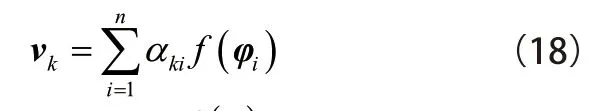
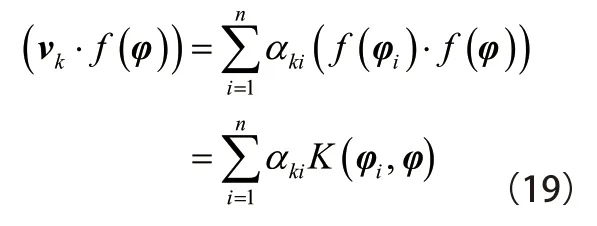
3.2 提取自回归系数中的环境分量

根据上一节分析，我们可以发现核主成分分析并不知道由样本空间到特征空间的非线性映射的具体形式。因此，它无法采用类似主成分分析的处理方法消除自回归系数中的环境分量，只能用于提取环境变量。

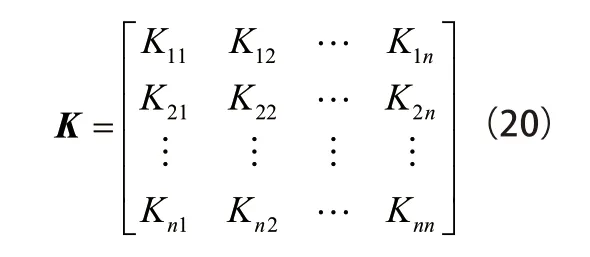
对K进行主成分分析，得到第一核主成分表达式为

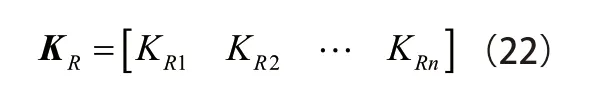
则待检样本的第一核主成分为

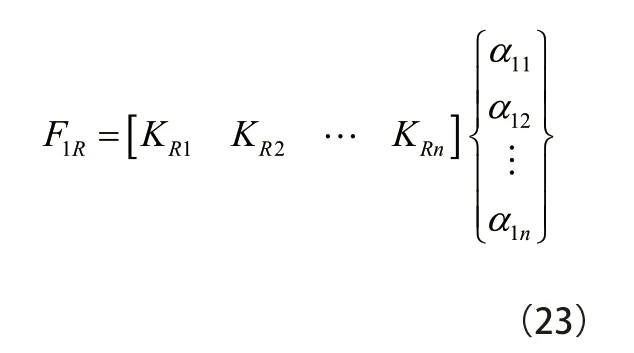
该方法间接实现了自回归模型法中环境因素的消除问题，特点是采用非线性的核主成分分析提取环境因素；可选择不同的核函数以达到最优结果。但是，该方法需要大量的参考样本组建一个相对比较完整的样本空间。

4 平胜大桥健康状况分析

平胜大桥是一座独塔单跨四索面自锚式悬索桥，如图1 所示。主跨为钢加劲箱梁，跨径350 m。主缆直径为440 mm，大桥宽度为2×26.1 m。主塔采用三柱式，塔高142.06 m。

图1 佛山平胜大桥

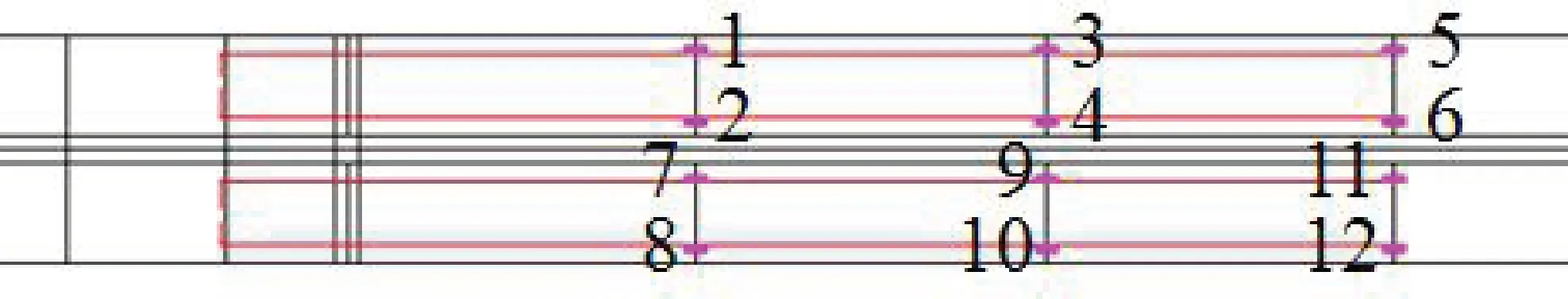
图2 桥面加速度传感器分布图

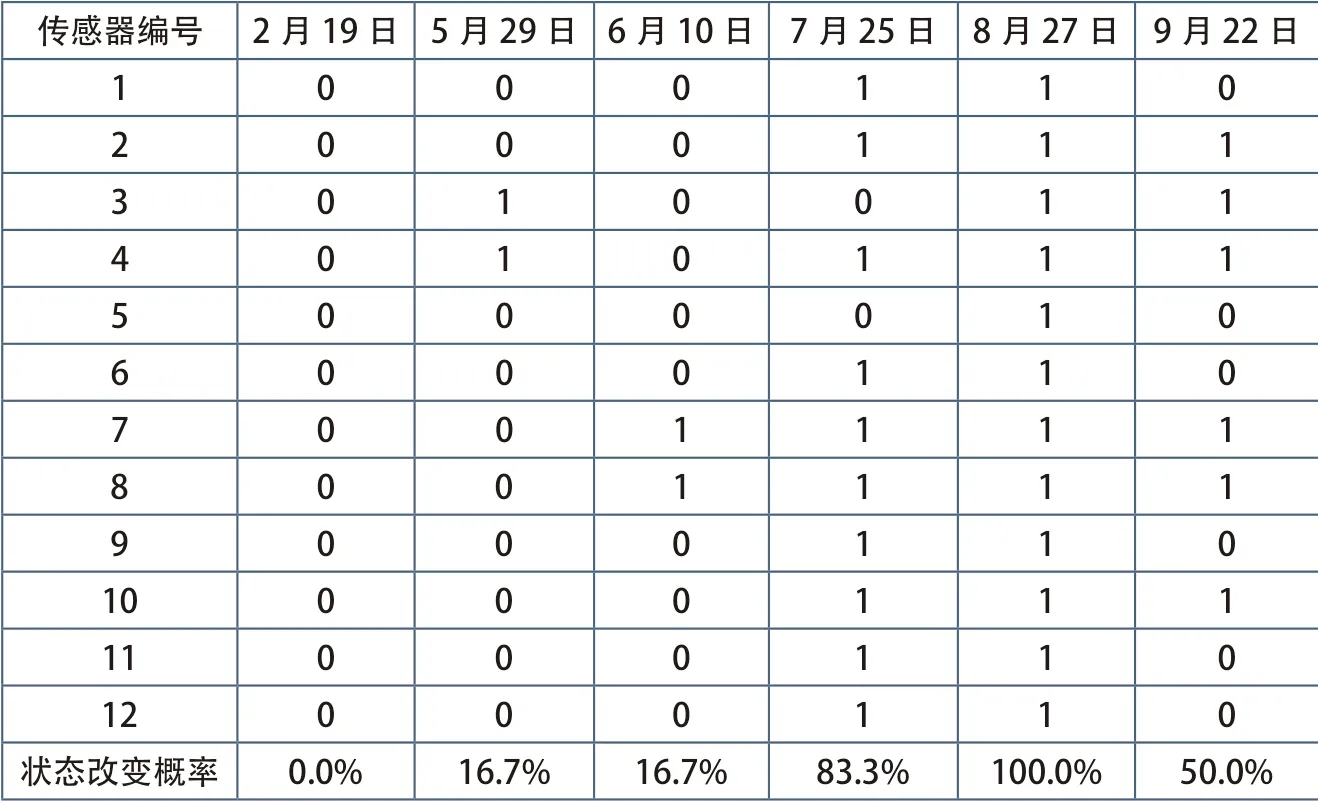
表1 基于自回归模型和主成分分析的健康诊断结果

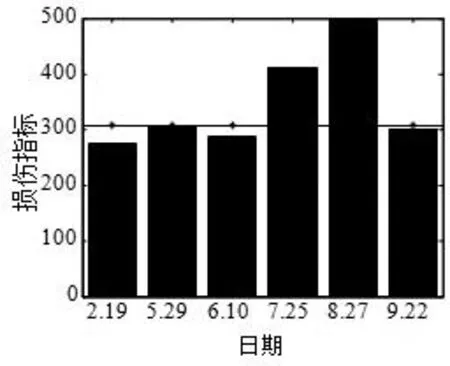
图3 1 号传感器损伤识别结果

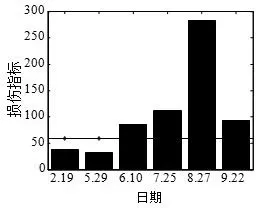
图4 7 号传感器损伤识别结果

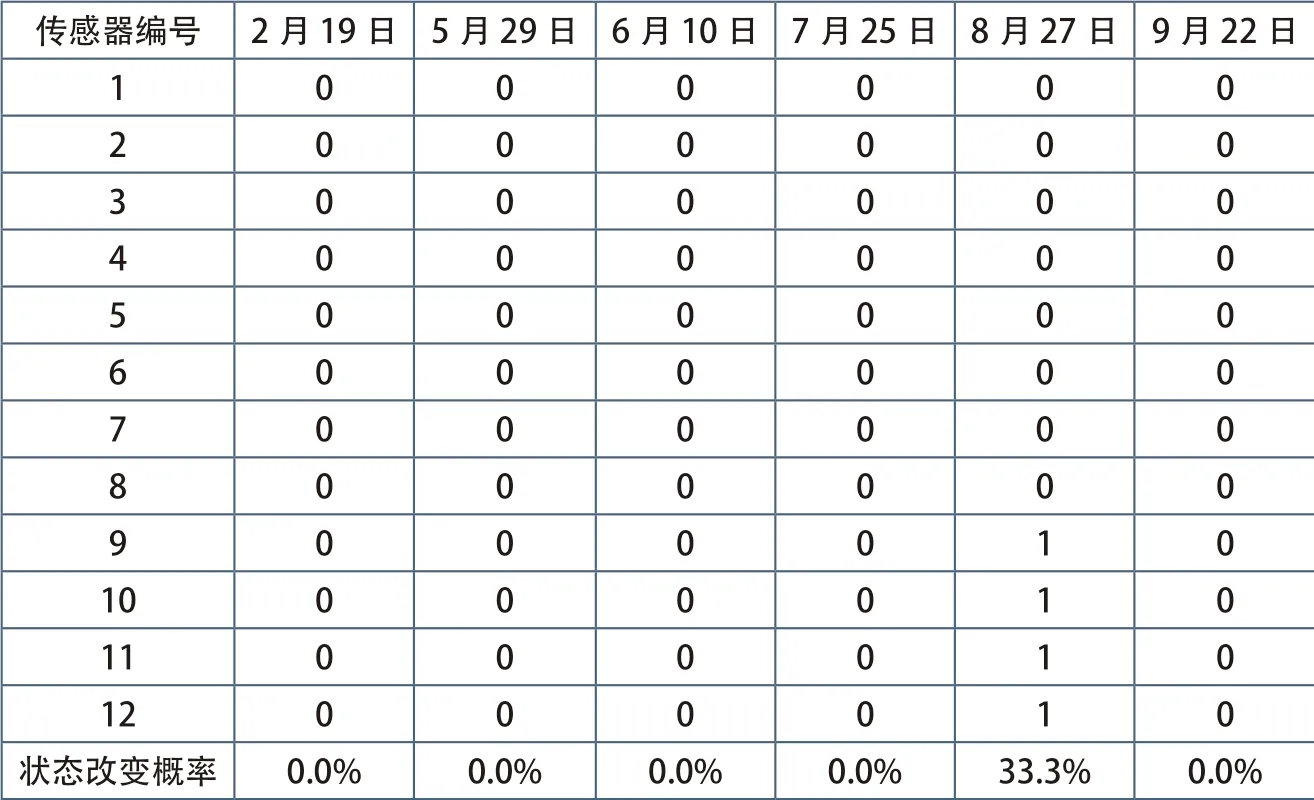
表2 基于自回归模型和核主成分分析的健康诊断结果

4.1 加速度传感器布点

全桥共安装有26 个加速度传感器，采样频率均为200 Hz。其中12 个位于桥面，4 个位于桥索，10 个位于桥塔。本文只研究桥面的加速度响应数据。如图2所示。

4.2 基于自回归模型和主成分分析的损伤诊断

应用基于自回归模型和主成分分析的损伤识别方法对平胜大桥前12 个传感器进行损伤识别，识别结果如表1 所示。表中0 代表健康，1 代表损伤。定义状态改变概率为判定为损伤的传感器个数除以参与判定的传感器总数。

分析位于桥面板的1 号、7 号传感器的损伤判定结果，如图3、4 所示。损伤指标先升高后减低，且均在8 月27 号达到峰值。从2 月份到8 月份，天气温度由低到高，即该方法误将温度升高判断为损伤，采用主成分分析没有消除自回归系数中的温度因素影响。从表中可以看出，7 月25 日、8 月27 日的状态改变误判率大于50%。

4.3 基于自回归模型和核主成分分析的损伤诊断

核函数选择高斯核函数，各传感器的损伤判定结果如表2 所示。从表中可以看出，除8 月27 日之外，各个日期的状态改变率为零，即没有产生误判。9-12 号传感器在8 月27 日产生误判，其原因尚待进一步查究。总体上，采用基于自回归模型和核主成分分析的损伤识别方法改善了基于主成分分析方法的识别结果，减少了误判率。

为验证该方法能消除温度因素影响，同样选取1 号、7 号传感器的损伤识别结果分析，如图5、6 所示。1 号传感器的损伤指标基本上没有变化，说明温度变化对损伤指标的影响已经消除，7 号传感器中除了7 月25 日的损伤指标偏大外，与1 号传感器类似。

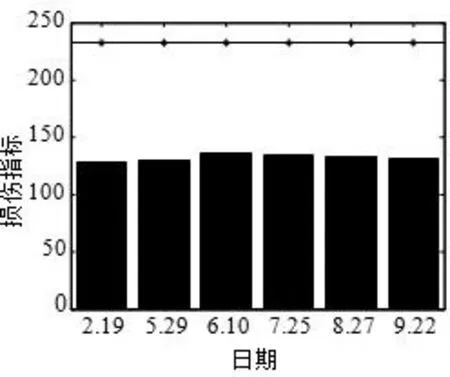
图5 1 号传感器损伤识别结果

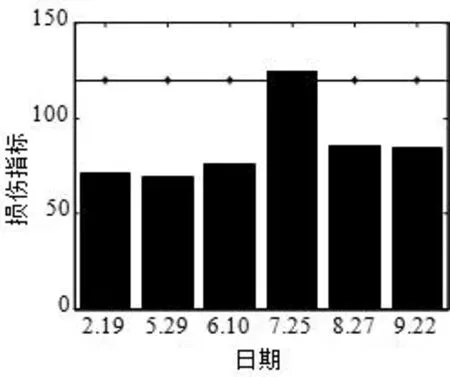
图6 7 号传感器损伤识别结果

5 结论

本文应用基于自回归模型和主成分分析、核主成分分析的损伤识别方法，以此消除结构损伤诊断中环境因素的干扰。通过佛山平胜大桥的实测桥面加速度数据，验证了核主成分分析比主成分分析更适用于实际工程中排除环境干扰。

本文还发现了以下几点有待研究的问题：

（1）实际工程结构中布置的传感器数量众多且功能各异，充分利用这些传感器的信息能够提高损伤识别精度。发展多传感器融合的损伤识别法是一个很有价值的研究方向。

（2）自回归模型属于线性模型，它无法描述结构的非线性特征，建模的误差会影响损伤诊断的结果。因此，建立非线性模型更符合工程实际。

（3）构造合适的损伤指标来降低其对环境的灵敏度也是消除环境因素影响的途径，但本文并未涉及。