群体性突发事件化解机制的随机演化博弈模型
宋民雪,刘德海
(东北财经大学管理科学与工程学院,辽宁 大连 116025)
1 引言
二十世纪九十年代以来我国社会结构处于快速转型期,我国群体性突发事件数量急剧增加,已经成为影响我国实现现代化和社会稳定的主要因素[1]。群体性突发事件[2-5]是指由社会矛盾引发的,由多人参与,为了实现一定的目的,采取集体上访、罢工、聚众闹事、游行示威、围堵政府机关等行为,危害公共安全[6-10],严重影响社会秩序的事件。群体性事件具有受随机因素干扰的突发性强、事态随着外部环境迅速演化、参与人群规模有限(从大于5人到上万人)、参与群体的利益诉求不完全一致等重要的管理学特征。2008年甘肃陇南事件、贵州瓮安事件、出租罢运事件,2009年通钢事件、湖北石首事件,2011年大连 “PX事件”,2014年云南晋宁征地惨案以及2017年嘉陵江污染事件等群体性突发事件。这些事件不仅威胁人们的生命财产安全,而且还会使人们心理产生恐惧和不安,使政府公信力下降[11]。如何化解群体性突发事件是政府长期面临的重要问题,如果政府处置不当,会出现抗议群众激增、非法集会、游行甚至打砸抢烧等行为,容易造成社会恐慌,甚至带来巨大的经济损失和政治影响。对于如何化解群体性突发事件,刘雪松和宁虹超[12]提出构建公正有序的社会治理模式,可以有效化解群体性突发事件。梅传强和胡江[13]提出政府应建立以保障民生为导向的社会矛盾化解机制,积极利用互联网平台,及时通过互联网平台回应、释疑,消除群众的困惑等方法来化解群体性突发事件。周方治[14]分别从长期、中期和近期三个角度提出群体性突发事件的化解路径,长期的根本路径在于建立“纺锤形”的社会形态;中期的根本路径在于建立权威的公力救济体系;近期根本路径在于建立规范的监管处置机制。群体性突发事件具突发性、各方利益的冲突对抗性、社会转移过程的长期性、后果的难以预测等特征。准确把握群体性事件属于人民内部矛盾的根本特征,在新时期成功处置并有效化解群体性事件,对于实现我国社会主义现代化的平稳过渡具有至关重要的意义。
群体性突发事件作为社会运动、社会冲突在中国社会转型期的一种特殊表现形式,引起了社会学、法学、政治学等领域研究学者的高度关注。进入21世纪以来,管理科学领域学者开始逐渐认识到群体性突发事件具有特殊中国管理情境的管理科学特征,并分别运用统计学、优化模型、演化博弈等方法研究群体性突发事件的产生机理和演变过程。首先,从实证分析角度上,张书维[15]运用统计学方法研究群众面临的群际威胁通过群体效能和群体愤怒的中介作用影响集群行为意向的双路径模型, 以及群体认同对双路径模型的调节效应。罗成琳和李向阳[16]分析了群体性突发事件演化的主要影响因素和指标,并且构建了群体性突发事件的演化机理的静态结构和动态流程,提出了一些预防群体性突发事件的建议。姜金贵等[17]运用扎根理论和结构方程模型研究了群体事件诱发因素及其关联关系。其次,从数理模型分析角度上,各种优化模型、系统动力学模型等优化和仿真方法是经常采用的分析工具。其中,刘德海和苏烨[18]建立了群体性突发事件的社会调解、警力防御和信息预警优化模型,分析了社会调解、警力防御和信息预警的最优策略。沈焱等[19]考虑政府采取部署警力和经济补偿应急策略,构建了环境污染群体性事件优化模型,建议政府在化解群体性突发事件时应根据事件发展的不同时期权衡部署警力和经济补偿应急策略。熊国强和赵昕[20]使用系统动力学方法构建了耦合情绪因素的群体性突发事件的演化模型,分析了群体性突发事件参与者在不同的情绪扰动下的行为演化路径,提出管理者需要及时监测抗议群众的情绪状态和变化,加强控制和疏导抗议群众的情绪变化,可以降低群体性突发事件产生的经济损失。也有一些学者从演化博弈角度分析和解决群体性突发事件。二十世纪九十年代,基于有限理性的演化博弈理论被提出,有限理性被表述成个体在对博弈局势的学习中确定动态演化的行为决策机制[21]。演化博弈理论将人的行为刻画为具有某种适应性学习能力的渐进演化过程,该研究范式为分析群体性突发事件演化规律提供了良好的理论途径。李勇建和王治莹[22]考虑舆情传播主体认知差异,构建了社会公众之间及社会公众与政府部门之间的演化博弈模型,并运用突发事件的结构化描述框架从属性层次对突发事件中舆情的产生和传播机制进行研究。刘德海等[23]考虑群体性突发事件中不同利益方同时存在着信息过剩、信息匮乏和虚假信息等信息特征,建立信息传播的演化博弈模型,分析了信息特征对事态演化的影响。谢百帅等[24]将政府作为社会矛盾的调解者,构建了政府作为社会矛盾调解者的演化博弈模型,研究表明政府提前介入、适当的惩罚能够有效的避免群体性突发事件的发生。
关于无限总体的演化博弈理论主要用复制动态模型[25]来刻画个体的模仿学习过程[26],但在现实生活中,社会行为的演化都是在有限总体中进行的,并且决策环境中有许多随机干扰因素,因此基于有限总体的随机演化博弈理论被提出。在有限总体的随机演化博弈理论中,应用较广泛的随机过程主要有Moran过程和Wright-Fisher过程。王先甲等[27]基于Moran过程分析了有限个消费者众筹策略演化动态,得出在强选择下,消费者人数小于某个临界值时,不参与众筹策略占优,在弱选择情况下,得出支出成本小于净收益的三分之一,众筹成功策略是演化稳定策略。
群体性事件具有很强的随机性和演化性特征,随机演化博弈理论提供了一种合适的分析方法。其中,陈业华等[28]考虑群体性突发事件和舆情之间的相互作用,构建了群体性突发事件舆情随机演化模型。王循庆等[29]将群体性突发事件的属性进行细分,分析其演化过程中的相关属性,建立了随机Petri网群体性突发事件情景演变模型和马尔科夫链模型。孙华丽等[30]分析了随机干扰下强势群体与弱势群体两个异质群体的策略选择的随机演化过程,基于复制动态方程分析了两个异质群体行为演化规律和稳定策略。但是,现有文献主要集中在群体性事件的发生和演化过程,但是目前尚未有应用随机演化理论对群体性突发事件的化解机制加以研究。本文借鉴了王先甲等学者关于随机演化博弈理论与应用的现有研究,建立了群体性事件化解机制的随机演化博弈Moran过程模型,研究了抗议群众选择退出抗议策略事件消退的必要充分条件。
2 群体性突发事件化解机制的理论模型
2.1 符号定义和基本假设
为了便于分析,本文出现的数学符号定义如表1所示。
在群体性突发事件应急处置过程中,地方政府部门回应抗议群众的合理诉求,同时坚持以法治手段解决问题,部分相对理性的抗议群体主要诉求得到满足,选择退出抗议策略,将退出抗议的该类群体定义为W群体。剩下处于非理性情绪中的抗议群众仍会坚持继续抗议,将该群体定义为A群体。为了尽快平息事件,地方政府可以通过提高经济补偿或者加大警力部署,继续抗议的A群体可能选择陆续退出,转化为接受处置方案的W群体。

表1 有关数学符号及定义
本文的基本假设如下:
假设1:地方政府与抗议群众共同争夺价值为V的经济资源,抗议群众总人数为N的有限群体,地方政府g为强势政府,拥有各种信息和行政权利,可以通过释放信号降低抗议群体的诉求期望。
假设2:在群体性突发事件平息的过程中,面对抗议群众的利益诉求,地方政府g可采取的策略包括:强硬D和妥协F,可行的策略空间Sg={D,F}而抗议群众j在面对政府决策时,可选的策略包括:继续抗议A和退出抗议W,可行的策略空间Sj={A,W}
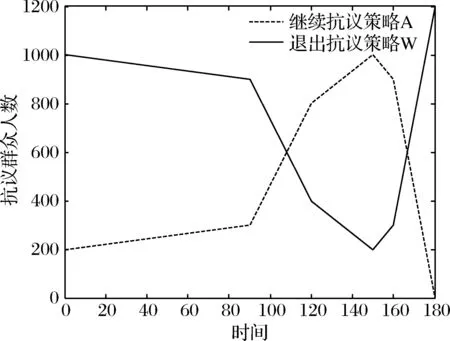
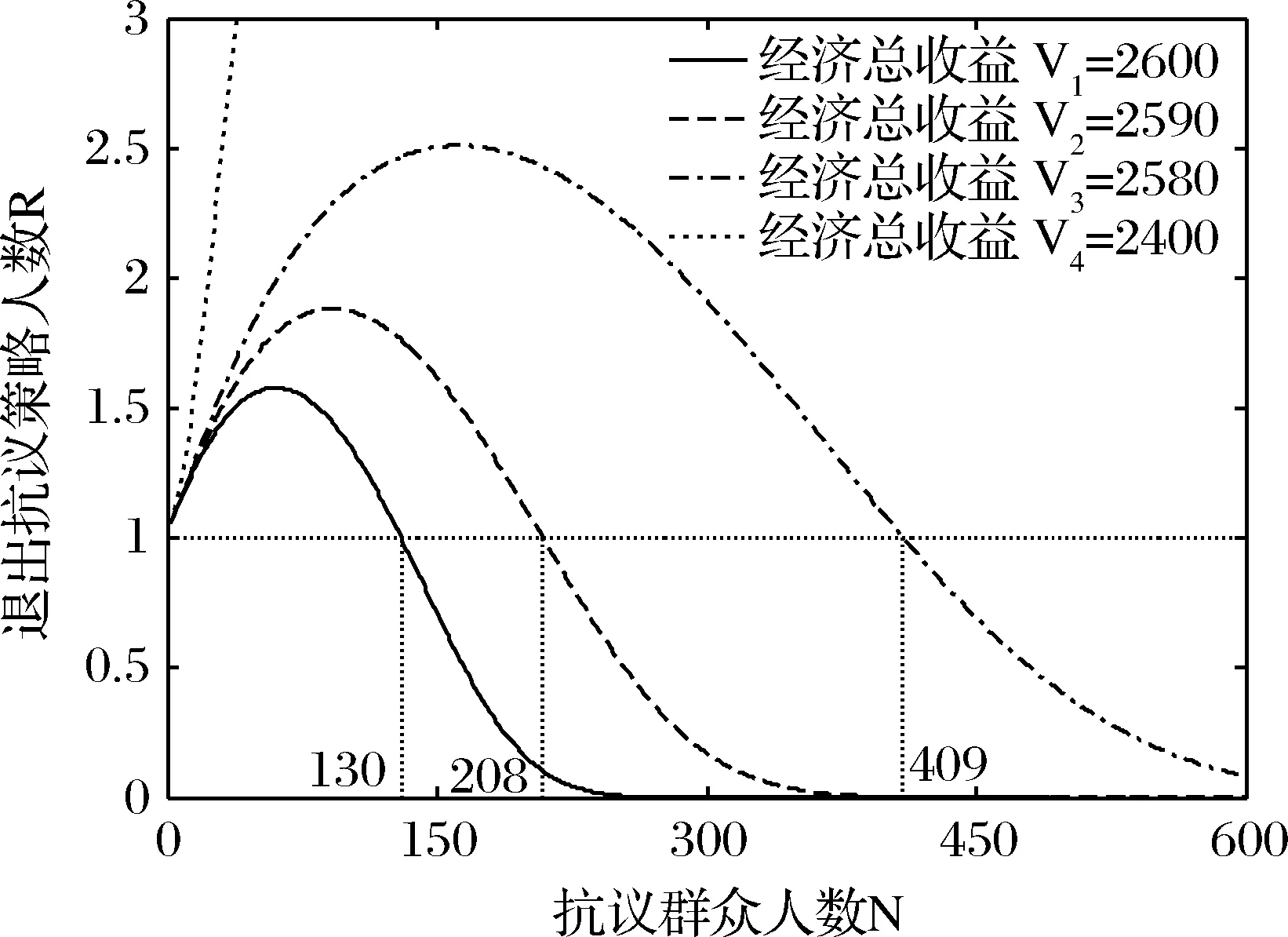
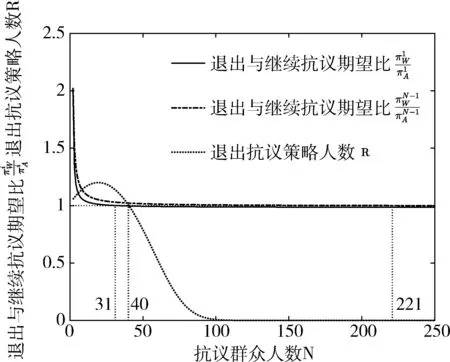
假设3:在地方政府g与抗议群众j博弈过程中,若地方政府g面对抗议群众j的利益诉求采取强硬D策略,而抗议群众j采取继续抗议A策略,双方在斗争过程中,将导致两败俱伤,会产生误工成本、时间成本等冲突成本C,其中0 假设4:在平息群体性突发事件过程中,地方政府对于选择退出抗议策略W的抗议群众给予补偿,记为B。 假设5:此过程为多阶段博弈过程,政府决策可以依据阶段的不同而不同,当政府方案满足抗议群众当期期望时,抗议群众便接受政府方案,退出抗议群体,反之,继续抗议。 表2 群体性突发事件的策略博弈模型 根据上述假设,可以得到群体性突发事件的策略博弈模型(表2所示)。分析该策略式博弈模型,当B 在演化博弈中,抗议群众作为有限理性的群体行为,具有较大的异质性。地方政府有效化解群体性突发事件,关键在于相对理性的抗议群众是否接受政府的处置方案退出抗议。当抗议群众作为一个整体产生分化,相对理性的部分群众退出后,剩余少数非理性的抗议群众将面临着依法处置等不利局面,无论是采取动用警力,还是被迫接受处置方案,事态发展将趋于收敛。因此,抗议群众的行动选择(退出抗议、继续抗议)和选择相应策略的人数规模,直接决定了事态的发展结果。本文将抗议群众收益作为研究对象,由表2可得到抗议群众的2×2对称支付矩阵表3: 表3 抗议群众策略学习的2×2对称支付矩阵 随机演化博弈Moran过程是一个生灭过程,有限人数的抗议群众在每一期策略选择过程中,随机选择一个抗议群众策略进行模仿,模仿的概率与抗议群众的效用函数成正比,被模仿的策略增加一个,新增加的抗议群众策略替换抗议群体中任何一个抗议群众策略,抗议群众总数量在这个过程中始终保持不变[31]。因此,基于Moran过程分析有限抗议群众策略选择,可以较好的体现抗议群众策略选择的随机性和动态性。 假设抗议群众总人数为N,选择退出抗议策略W的人数为i,则选择继续抗议策略A的人数为N-i。那么,选择退出抗议策略W和选择继续抗议策略A的期望收益分别为: i=1,2,…N-1 (1) i=1,2,…N-1 (2) 在经典的演化博弈动力学框架下,我们使用效用函数来衡量抗议群众选择某种策略所占比例的增长率,每个策略的效用函数与其期望收益有关,但在社会经济系统中,群体参与者的效用函数还受其他随机因素的影响,如:抗议群众非理性情绪等系统内部未考虑的因素、影响事态发展的随机事件干扰等外部不确定性因素等。为了与实际复杂的决策制约条件更好地契合,我们把这些其他影响因素简化成选择强度参数β,进而可以得到退出抗议策略W和继续抗议策略A的线性效用函数为[32]: (3) (4) 其中0≤β≤1。当β→0时,称为弱选择,此时参与者选择不同策略的效用函数均趋近于固定值1,期望收益的影响不大。当β=1时,称为强选择,此时效用函数完全由期望收益决定,而与其他随机因素无关,即抗议群众决策是否继续抗议,只与抗议群众获得的期望收益有关。 由Moran过程可以得到,在有限个参与者的抗议群体中,当所有参与者均面临决策的时候,选取继续抗议策略A的抗议群众,接受政府方案改为选择退出抗议策略W,即选取退出抗议策略W的抗议群众人数增加一个的概率,可以表示为: (5) 同理,选取退出抗议策略W的抗议群众,改为选取继续抗议策略A,即选取退出抗议策略W的抗议群众人数减少一个的概率,可以表示为: (6) 当所有的抗议群众均采取观望的态度,保持上一轮策略不变,即选取退出抗议策略W的抗议群众人数保持不变的概率,可以表示为: Pi,i=1-Pi,i+1-Pi,i-1 (7) 在抗议群众策略演化的过程中,选择退出抗议策略W的抗议群众人数可能增加一个,减少一个或者不变。并无其他策略选择,故而退出抗议策略W从状态i转移到其他状态的概率为0,则有Moran过程的一步转移概率矩阵如下: (8) 上述Moran过程有两个稳定状态,即i=0,i=N。即所有的抗议群众都选择继续抗议策略A或者都选择退出抗议策略W。如果抗议群体一旦达到这两个状态,在外部环境不变的条件下,则抗议群体策略将处于稳定状态,此时演化过程停止。政府部门需要在尽可能短的时间内,迅速平息群体性突发事件,保障公众的生命和财产安全,维护社会秩序稳定。群体性突发事件平息的标志,即采取继续抗议策略A的抗议群众均采取退出抗议策略W,达到i=N的稳定状态。 在演化博弈过程中,会基于政府策略及抗议群众的对应策略找出演化方向,即主要考量政府在不同时期、不同策略下,抗议群众的策略动态选择,进而由公式(5)和公式(6)可以得出,退出抗议策略W减少一个的概率与退出抗议策略增加一个的概率之比为: (9) 如果比率接近于0,那么选择退出抗议策略W的抗议群众人数增加的可能性就越大,此时事态趋于平息。如果比率非常大,那么选择退出抗议策略W的抗议群众人数可能会减少,事态发展趋于扩大化。如果比率等于1,那么选择退出抗议策略W的抗议群众人数增加和减少的可能性是相同的。 下面计算收敛到两个稳态的概率,令xi表示从状态i到状态N的概率,即最初有i个选择退出抗议策略W的抗议群众和N-i个选择继续抗议策略A的抗议群众,最终演化成N个抗议群众全部选择退出抗议策略W的概率。因此易得x0=0,xN=1,而对于0 xi=Pi,i-1xi-1+Pi,ixi+Pi,i+1xi+1 (10) 将式(5)、式(6)、式(7)代入式(10)有: (11) 考虑最初只有一个抗议群众选择退出抗议策略W,其余N-1个抗议群众均选择继续抗议策略A,最终演变成N个抗议群众均选择退出抗议策略W的概率,称为退出抗议策略W的固定概率,记为ρW。同理,最初只有一个抗议群众选择继续抗议策略A,其余N-1个抗议群众均选择退出抗议策略W,最终演变成N个抗议群众均选择继续抗议策略A的概率,称为继续抗议策略A的固定概率,记为ρA,由(11)式得: (12) (13) 因此,由式(12),式(13),参照文献32,我们可得出抗议群众选择退出抗议策略W与继续抗议策略A的固定概率之比,详见如下命题。 命题1:基于Moran过程的群体性突发事件随机演化博弈模型中,抗议群体选择继续抗议策略A与退出抗议策略W的固定概率比值为: (14) 在经典的确定性演化博弈理论中,抗议群众的效用函数完全由期望收益决定。但是,在群体性突发事件的演变过程中,抗议群众的效用函数并不是完全由期望收益决定的,还会受到系统外部各种不确定性因素、抗议群众内部的非理性情绪等因素影响。如果各种内外部随机性影响因素发挥着主导作用,将导致抗议群众的策略选择完全取决于内外部的随机因素,效用函数趋近于外部随机性因素决定的某个固定值,而与选择不同策略的期望收益无关,此时即为弱选择过程。 考虑在弱选择条件下,即β→0时,将式(12)、式(13)在β→0处进行泰勒展开,有 (15) (16) 命题2:基于Moran过程的群体性突发事件随机演化博弈模型中,在随机性因素占据主导地位的弱选择作用下,当有关收益满足如下条件时,抗议群体选择退出抗议策略W将成为稳定的均衡,群体性事件得到有效化解: 6B(N-1)+2C(N+1)>3V(N-2) (17) 分析上式可知,冲突双方争夺的经济资源V越小,政府补偿额B和冲突成本C越大,群体性突发事件中抗议群体将选择退出抗议策略,事态趋于平息。 推论1:在随机性因素占据主导地位的弱选择作用下,群体性突发事件能够有效化解的最大规模为: (18) 通过命题2可知,政府在处置群体性突发事件过程中,政府应当对于有不合理诉求、煽动群众抗议、扰乱社会秩序甚至有过激行为的群众,给予一定的处罚,以达到增加抗议群众冲突成本的目的。同时,针对群体事件中的少数持续不放弃抗议的抗议群众,应该特殊情况特殊对待,给予他们额外的补偿,促使他们退出抗议。此外,对于抗议群众和政府争夺的经济资源,如:拆迁改造的居民住宅、征用的农村土地、改制的国有企业等经济资源,政府应按照市场资源评估的较低标准来评估经济资源的价值,而不要给予过高的评估价值。通过上述方法可以促使群体性突发事件化解。 通过推论可知,当随机性因素占据主导地位时,有效化解群体性突发事件的一个关键因素是参与抗议活动的规模。只有当一定规模下,事态才有可能朝着有效化解的方向发展。否则,一旦超过临界规模,事态将变得难以控制。 在强选择条件下,即β=1,效用函数完全由期望收益决定,即抗议群众决策是否继续抗议完全由期望收益决定,不会受其他因素的干扰。将每一状态i下的两策略的效用函数进行比较,用hi来表示两策略的效用函数之差,从而可以判断选择行为是否会降低或者提高某一策略抗议群众的数量。具体表示为[33]: hi=fi-gi,i=1,2,…N-1 (19) 若h1>0,则称选择支持退出抗议策略W入侵继续抗议策略A;若hN-1<0,则称选择支持继续抗议策略A入侵退出抗议策略W。 由公式(1)、公式(2)代入公式(19)可得: (20) (21) 命题3:基于Moran过程的群体性突发事件随机演化博弈模型中,在排除了随机性因素干扰的强选择作用下,当抗议群体的规模满足如下条件时,抗议群体选择退出抗议策略W将成为稳定的均衡,群体性事件得到有效化解: (22) 由命题3可知,在排除了随机性干扰因素的强选择条件下,抗议群众选择继续抗议策略A还是退出抗议策略W与抗议群众数量N有关,如果给定冲突成本、经济资源和政府补偿,那么存在一个临界值[Nmax|β = 1],当抗议群众人数N≤[Nmax|β = 1] 时,抗议群众为获得更高的收益,都会选择退出抗议策略W,退出抗议策略W将成为演化稳定策略。因此政府在处置群体性突发事件时,地方政府应该把握事态初期阶段参与抗议的群体规模较小的窗口期,提高社会补偿措施,加大对“打砸抢”等违法行为的惩处,从而有利于事态的化解。 命题4:基于Moran过程的群体性突发事件随机演化博弈模型中,当抗议群体选择退出抗议策略W将成为稳定的均衡,比较随机性干扰占据主导地位的弱选择过程β→0和排除了随机性因素的强选择过程β=1,后者具有更小的临界抗议群众规模,即Nmax|β = 1< Nmax|β→0。 命题4表明,当群体性事件的内外部随机性干扰因素影响较小,抗议群体的利益诉求集中在经济利益方面时候,由于冲突目标比较明确,地方政府需要及早介入及时采取化解措施,从而在临界规模之前平息事态。如果事态受到了随机性因素的主导,由于事态可控的临界规模更大,地方政府需要摸清情况,不能贸然采取经济补偿的手段以产生不良的示范效应。 按照东莞市统一规划方案,2011年C村被东莞市政府纳入市重点项目规划用地,征用C村183亩土地用来建设东莞市政府重点项目。C村有权获得征地补偿的人数约1200人,依照《广东省征地补偿保护标准》,东莞市政府给予每亩约7万元的征地补偿,C村村民认为政府给予的补偿过低,和地方政府进行5天的协商谈判,未能达成一致。在项目施工过程中,村民进行非法聚集,项目开工当天,就有大约200人到施工现场聚众闹事,阻碍项目进行。C村公安局最初派出150名警察到施工现场维护秩序,由于抗议群众情绪激动,不听执法人员的劝阻,并且攻击执法人员。抗议群众不断增多。由于现场警力有限,人数不占优势,无法稳定现场局面,C村公安局向东莞市公安局请求警力支援,东莞市公安局接到支援请求,立即派出特警队到施工现场增援。大约30分钟后特警队到达现场,此时抗议人数达到最大值,经过30分钟,最终抗议群众被成功驱散,事件得以平息[34]。在此次事件处置过程中,抗议群众和执法人员均有受伤。 图1 抗议群众策略演化随时间变化的趋势图 根据案例可知,政府补偿B=1281万元。根据2011年东莞市国民经济和社会发展统计公报[35],东莞市农村村民人均纯收入22842元,1200名村民5天的集体冲突成本C≈38万元。重点项目带来的经济总收益V具有较强的不确定性,如:项目评估过程中可能会出现政府政策、法规的变化、自然灾害、通货膨胀产生的物价浮动等难以计量的因素和未知因素,因此本文将此设为关键的待定参数,进行敏感性分析。 图2 不同社会资源下总人数N与退出抗议策略人数R关系图 在弱选择情况下,这里假定β=0.0001,考虑不同的经济总收益V对抗议群众策略演化的影响,通过比较退出抗议策略的人数R=NρW的大小来判断策略演化方向,若NρW>1,即退出抗议策略W将成为演化稳定策略;若NρW<1,即继续抗议策略A将成为演化稳定策略。根据抗议群体退出抗议策略的固定概率公式(3)、(4)和(12),代入本案例有关数值后,可得图2所示的总人数N与退出抗议策略人数R的关系。 由图2可知,随着经济总收益V逐渐减小,临界抗议群众规模逐渐增大。当经济总收益V在一定范围内,抗议群众人数存在一个临界值,当抗议群众人数小于该临界值时,退出抗议策略W占优,当抗议群众人数大于该临界值时,继续抗议策略A占优。当经济总收益V较小时,不论抗议群众人数多少,始终是退出抗议策略W占优,即退出抗议策略W将是演化稳定策略。 在经济总收益分别为V1=2600,V2=2590,V3=2580时,根据公式(12)和NρW>1,可求得临界抗议规模分别为130,208,409。即当经济总收益V1=2600时,在0 图3 抗议群众人数N与h1,hN-1,R关系图 随着我国社会经济系统的快速转型,各种人民内部矛盾引发的群体性突发事件不仅给人们的人身和财产安全造成了威胁,而且还会使社会秩序不稳定。有效化解群体性突发事件等重大社会风险成为当前我国政府面临的一项重要的社会任务。本文首次将Moran过程应用到化解群体性突发事件中,研究群体性突发事件中有限抗议群体策略的演化动态,构建了化解群体性突发事件的随机演化博弈模型。 在平息群体性突发事件过程中,抗议群众采取退出策略或继续抗议策略将导致事态不同的演化方向。本文根据抗议群体的行动分化导致事态平息的思路,提出了化解群体性突发事件随机演化博弈模型,并分别探讨了在不同强度的随机因素(即弱选择和强选择条件)下,抗议群体策略向退出抗议策略演化的条件,最后以东莞市征地补偿事件进行案例研究。研究发现:基于Moran过程的群体性突发事件随机演化博弈模型中,系统的随机性越小,冲突双方争夺的经济资源越小,政府补偿额和冲突成本越大,群体性突发事件中抗议群体退出抗议的固定概率越大,事态趋于平息。抗议群众规模存在着一个能够成功化解的临界值。考虑随机性干扰占据主导地位的弱选择过程和排除了随机性因素的强选择过程,后者具有更小的临界抗议群众规模。上述研究结论可以为地方政府有效化解群体性突发事件提供丰富的管理启示。例如,参与抗议的群体规模是事态成功化解的重要因素,因此在群体性事件爆发的初期阶段,外部随机性因素和参与群体规模均较小,在此萌芽阶段地方政府应该加大处置力度;地方政府坚持法治渠道的化解原则,加大对“打砸抢”违法行为的惩罚力度,反而有利于事态的化解等等。 本文探讨群体性突发事件中抗议群体策略选择的演化过程,本文研究还可以进行一些拓展,比如本文没有考虑具体的随机干扰因素,在未来的研究中,可以将影响群体性突发事件的干扰因素进行细分。同时,根据不同的随机因素特征可以引入Wright-Fisher随机过程进行研究。考虑到群体性突发事件化解机制除了地方政府与当事群众进行直接沟通外,还可以通过依靠法治途径等第三方介入。此外,本文研究不仅适用于群体性突发事件问题,而且对反恐和制造商生产等相关问题具有一定的借鉴意义。

2.2 群体性突发事件化解的Moran过程模型

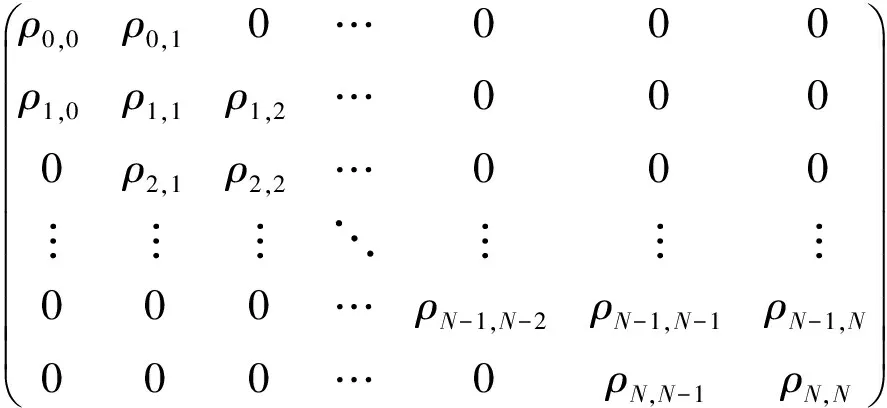
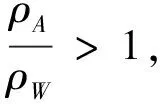
3 演化选择强度对事件化解机制的影响
3.1 随机性因素主导作用下的弱选择分析
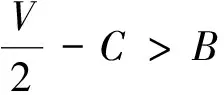
3.2 排除随机性因素的强选择分析

4 案例分析:东莞市C村征地补偿事件
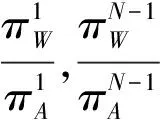
5 结语

