基于金融随机波动模型的快速MCMC算法研究

许健森，李城恩，施建华

（闽南师范大学数学与统计学院，福建漳州363000）

金融资产价格的波动率作为收益率变异程度的估计量，在金融资产配置、金融资产定价以及金融风险管理等问题上有着十分重要的作用，对波动率的研究一直是国内外金融领域聚焦的问题.金融市场的波动率往往呈现复杂多样的特性，大量文献研究表明，波动率存在着时变性与聚集性的特点.现有的两类能够较好地刻画这种特征的是Bollerslev[1]在Engle[2]提出的ARCH 模型基础上，加入条件异方差构造的广义自回归条件异方差（GARCH）模型以及Taylor[3]采用随机过程理论来刻画方差时变性特征的随机波动（SV）模型.由于随机变量的引入，SV模型相比GARCH模型具有更高的灵活性以及对金融数据有更好的拟合效果，因此SV模型在实际中被广泛应用.

在参数估计方面，由于SV 模型的似然函数是无解析解的多重积分，因此极大似然估计方法不再适用，模型的参数估计通常采用拟极大似然估计方法（QML）[4-5]、广义矩估计方法（GMM）[6]和马尔可夫链蒙特卡洛估计方法（MCMC）[7-13]等估计方法.其中GMM 方法在持续性参数接近于1 时，收敛于无条件矩的速度十分缓慢，而QML 方法在方差系数较小时，其有效性迅速降低.目前主流的方法是使用基于贝叶斯估计方法的MCMC 算法，该算法将给定的先验信息以及样本信息融合后进行贝叶斯统计推断，从而得到收敛于真实值的样本统计量.

在估计SV 模型参数时，一般采用MCMC 算法进行参数估计，该算法涉及的抽样方法多种多样，其中主要是Gibbs 抽样[7]以及Metropolis-Hastings 抽样[8]（以下简称为MH 抽样）.其中Gibbs 抽样仅适用于参数后验分布为常用的概率分布的参数估计，而MH抽样具有一般性，又可以分为独立MH抽样以及随机游走MH 抽样等，能够用于参数后验分布为复杂不常用的概率分布；在估计波动率方面，1994 年，Carter 和Kohn[9]以及Frühwirth-Schnatter[10]使用基于卡尔曼滤波的FFBS 算法进行波动率抽样，由于波动序列是序列相关的，故联合抽样更加有效.1994年，Carter和Kohn[9]使用的随机误差有限混合正态近似误差项比正态近似误差项的估计精度更高.基于此，为了提高MCMC 算法估计速度，我们对MCMC 算法进行了改进.在对感兴趣的参数进行抽样时，采取比“逐一”运算时间更快的“成块”联合抽样.而在波动率序列抽样的过程中，根据Mccausland 等[14]提出的MMP 算法，通过对波动率序列矩阵的精度矩阵进行Cholesky 分解，再利用分解结果进行矩阵运算，将波动率序列联合抽样出来，从而减少抽样耗时.因此，我们主要在有限混合正态近似的基础上结合MMP 算法以及参数联合抽样提出快速的MCMC 算法（Fast MCMC，简称为FMCMC）.

1 随机波动模型

标准的随机波动模型形式为：

其中t = 1,2,…,T，yt为t 时刻所持有的资产对数收益率，ht为t 时刻收益率的对数波动率，服从高斯AR(1)

过程，参数φ 用于度量波动率的持续性，在参数约束 |φ |＜1 下，波动率过程是平稳的，随机扰动项满足εt～N(0,1 ),ηt～N(0,σ2)，且εt与ηt相互独立.需要估计的参数μ 为波动率的平均趋势，φ 为波动率的持续性函数，其取值范围为(-1,1 )，σ为误差项ηt的方差，ht为需要估计的波动率.

在SV模型中，观测方程（1）是非线性的形式，这为模型的参数估计增加了难度，为了简化我们的估计过程，首先对观测方程（1）进行对数平方变换，即

其中const =0.000 1 是为了避免对数定义域问题，因此（1）式等价于

2 FMCMC算法

根据转换后的线性状态空间模型(6)、(7)，我们可以给出FMCMC 算法：首先初始化参数θ =(μ,φ,σ)′以及波动率ht；其次借鉴Omori 等[15]抽取变量st= j，st= j 代表正态分布混合逼近在t 时刻所使用的第j 个正态分布；接着结合MMP 算法波动率H=(ht,…,hT)′；最后抽取参数θ =(μ,φ,σ)′.重复执行上述步骤直至参数估计值收敛，具体抽样细节如下.

2.1 波动率H=(ht,…,hT)′的抽取

对于隐含波动率ht的抽样，目前已有几种高斯仿真抽样方法，其中，大部分是基于卡尔曼滤波的，但卡尔曼滤波算法需要大量的迭代计算，其计算成本较高，计算速度缓慢，因此为了改进估计速度，在抽取波动率ht过程中，应用Mccausland 等[14]中的MMP算法提高MCMC抽样的估计速度.这是因为MMP算法利用带对角结构对精度矩阵进行Cholesky 因子分解，通过矩阵运算对波动率ht进行抽样，从而实现高效的抽样.与卡尔曼滤波相比，MMP算法使用矩阵运算进行H的联合抽样，不需要用到迭代算法，因此在该步骤中节省了大部分的时间，从而提高了MCMC的抽样速度.下面结合SV 模型介绍我们所使用的MMP算法，MMP算法的实现基于一个重要的理论基础，即Mccausland 等[14]中的结论2.1.

记

通过Mccausland 等[14]中的推导方法，结合模型(6)和(7)可推导出形如上式的Ω与C.

其次，对精度矩阵Ω 进行Cholesky 分解，即找到一个对角元为正数的下三角矩阵L，使得Ω = LL′. 根据性质可知H|Y ～N(Ω-1C,Ω-1)，若记ξ ～NT(0,IT)，则有L′H = L-1C + ξ，再将该式两边同时左乘以(L′)-1即可求得隐含波动率的抽样公式为H =(L′)-1(L-1C + ξ ). 这样，通过MMP 的方法利用矩阵的运算对H=(ht,…,hT)′波动率序列进行联合抽样，从而提高了估计速度以及准确度.

2.2 参数θ =(μ,φ,σ)′的抽取

若分别对μ、φ、σ 进行逐个参数的抽样，这会增加MCMC算法的耗时，为了提高估计速度以及准确度，采用联合抽样的方式对θ =(μ,φ,σ)′进行联合抽样，为了避免θ 的联合分布的高斯截断问题，对参数值进行以下变换：

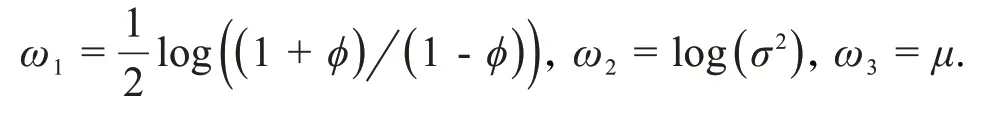
那么，变换后的新参数取值范围均为实数集ℝ.记新参数向量为ω =(ω1,ω2,ω3)′，假设参数向量ω 的联合密度函数为fω(ω1,ω2,ω3)，则参数向量θ 的联合密度为

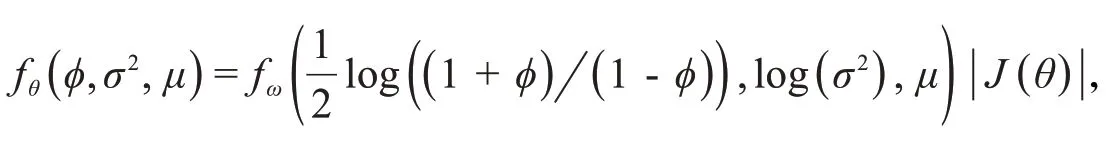
由于ω 的联合密度分布是多元的形式，并对参数空间θ 进行了变换，Gibbs[7]抽样不再适用，因此采用更一般性的MH抽样[8]算法，其建议分布为N(ω*,Σ*)，其中，ω*= ωold为前一次抽样接受的参数估计值，Σ*为主对角线为0.1、其余位置为0 的高斯分布协方差矩阵.记ωnew为建议分布产生的候选样本，fN(⋅)为高斯正态分布的密度函数，θold为前一次抽样的ωold通过逆变换得到的原参数向量，θnew为ωnew通过逆变换得到的原参数向量，参数后验密度π(θ|⋅ )= L(θ )π(θ )，L(θ )为SV 模型的似然函数，则MH 抽样的接受概率如下：

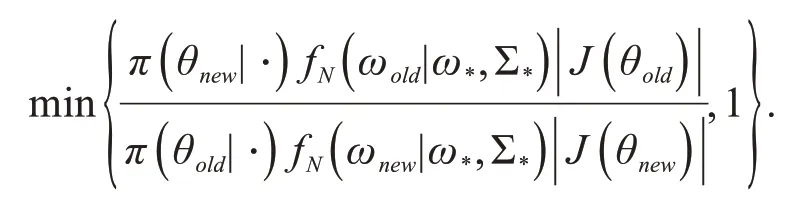
3 模拟与实证研究

3.1 数值模拟

根据提出的FMCMC 算法，我们对SV 模型进行参数估计，通过模拟生成不同时间长度以及参数真实值的模拟数据，进行数值模拟实验.而算法的优劣性方面，主要从估计准确度以及估计时间进行比较.我们的数值模拟实验室是通过R（3.5.3）软件，使用Rcpp、coda以及RcppArmadillo进行R与C++编程.

3.1.1 FMCMC算法与其他MCMC算法对比

为了验证所提出的FMCMC 算法的准确度以及估计效率，将FMCMC 算法与目前较为流行的Gibbs[7]算法（利用Winbugs[16]实现）以及Hoffman[17]提出的基于MH 算法改进的Naive No-U-Turn 算法（以下简称NNUT 算法，利用R 语言Rstan 包实现）进行比较，在表1 中给定的参数真实值情况下，产生时间长度T=1 000 的模拟数据中，进行预热1 000 次，以及5 000 次的MCMC 抽样. 对于先验分布，我们借鉴Kastner等[18]，选择如下的先验分布：

表1 中，μtrue，σtrue，φtrue分别表示模拟数据的参数真实值，在FMCMC、NNUT 以及Gibbs 下的数字为与之对应的参数估计值，括号内数字为参数估计值的标准差.在估计准确度方面，提出的FMCMC算法估计误差为，Rstan包中算法的估计误差为，Gibbs算法由于Winbugs显示精度问题，其估计误差为因此FMCMC 算法具有较好的估计精度以及准确度；在参数估计值的方差方面，Gibbs算法的方差最大，而NNUT 算法的方差最小，提出的FMCMC 在方差在两者之间，尽管FMCMC算法的方差不是最小的，但其估计效果仍然是不错的；在计算耗时方面，FMCMC算法的估计时间只需要5.26 s，NNUT算法需要58.92 s，Gibbs算法需要51.33 s，由此可见在计算速度方面，提出的FMCMC算法具有明显的优势，耗时仅为其它两种MCMC 算法耗时的10%，这种优势会随着时间序列的长度以及抽样次数的增加而更为明显.因此，FMCMC 算法在估计准确度、估计方差以及抽样耗时等方面更优于其它两种MCMC算法，能够较为准确地并快速地进行模型的参数估计.

表1 FMCMC算法与其他MCMC算法的估计结果Tab.1 Estimation results of FMCMC algorithm and other MCMC algorithms

3.1.2 FMCMC算法估计情况

由上可知FMCMC 算法的估计结果以及耗时是比较好的，在这一小节中我们通过设置的不同参数值以及不同的时间长度进行模拟分析，测试FMCMC算法在不同参数真实值下的估计情况(表2)，在表2中T为模拟数据的时间序列长度，其它符号以及数值说明与表1相同，由实验结果可知大部分参数估计误差均小于等于0.05，只有极少数的参数估计绝对误差小于等于0.09，因此FMCMC 算法的估计效果是相当不错的.

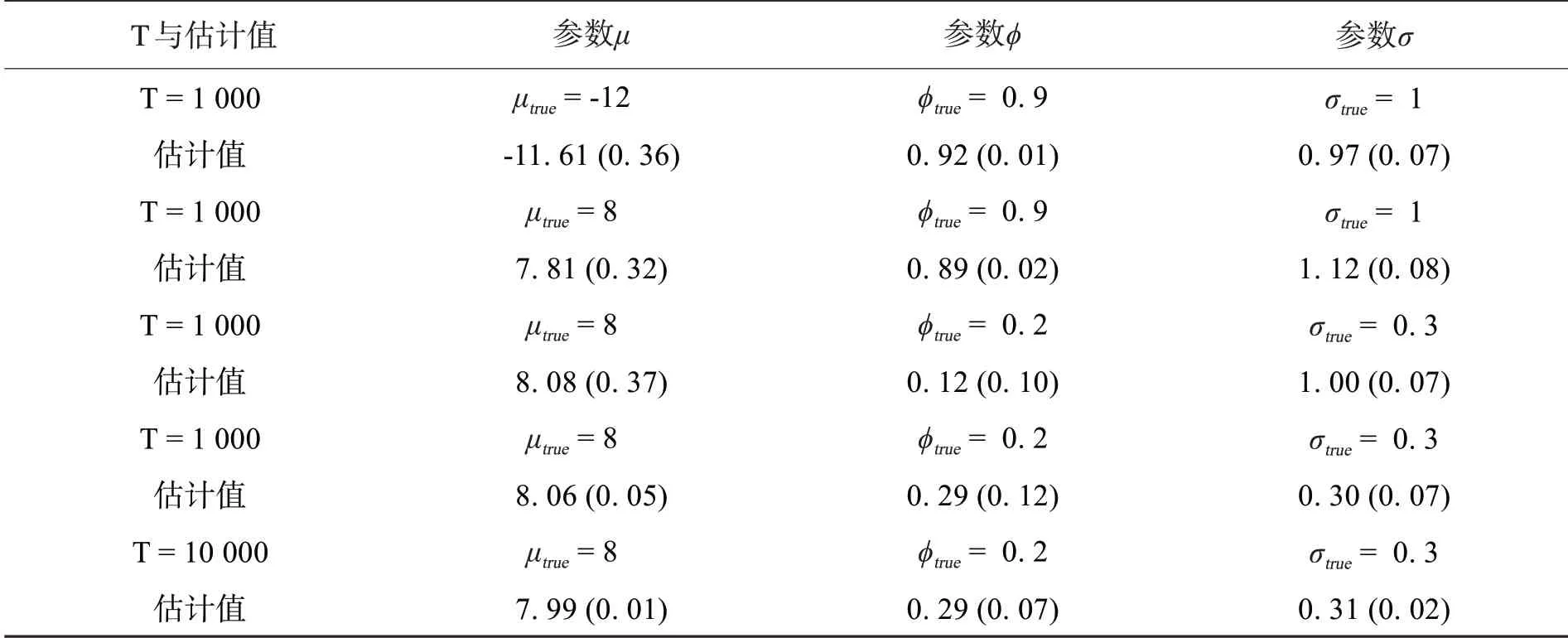
表2 不同参数不同时间长度模拟数据的FMCMC估计结果Tab.2 FMCMC estimation results of simulated data with different parameters and lengths

3.2 实证研究

沪深300股指具有较好的代表性，其发展趋势可以相当大程度地反映我们股价的总趋势，因此我们选取沪深300股指2005年1月4日-2019年5月31日数据建立随机波动模型进行分析，数据来源于网易财经网，共有3 501 个观测样本，为了便于分析，将处理后的数据扩大100 倍，即yt= 100×(lnPt- lnPt-1)，下面通过图1的对数收益率时序图以及描述统计表3对沪深300股指的波动特征进行初步地分析.

表3 沪深300股指对数收益率的统计特征Tab.3 Statistical characteristics of logarithmic yield of Shanghai and Shenzhen 300 stock index

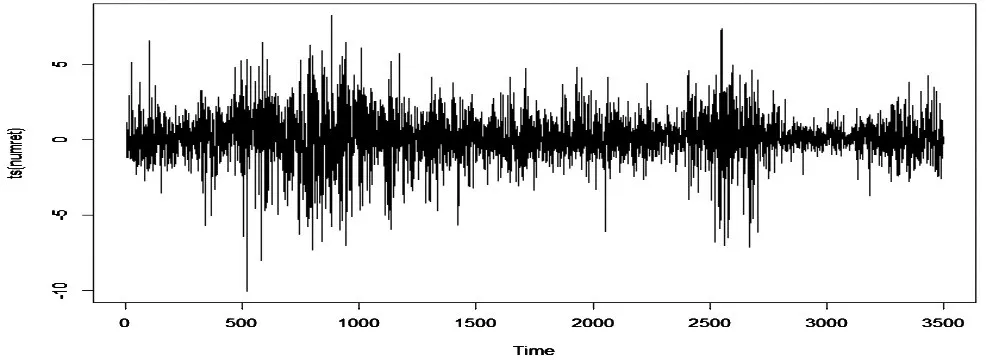
图1 沪深300股指对数收益率时序图Fig.1 Sequence diagram of logarithmic yield of Shanghai and Shenzhen 300 stock index

由图表可知其偏度小于0 且度大于3，通过JB 检验，其p 值远小于0.01，这说明了该数据特征是显著有偏且厚尾的，表明该数据适合用随机波动模型进行建模分析，因此可以采用我们的FMCMC 算法进行估计.结果如表4，其中MC 误差为其中s2为抽样方差，M 为抽样样本总数，IF 为低效率因子为在0处的谱密度估计值）.若MC 误差值越小，则说明该模型的估计结果更为准确.根据表4 可得出结论如下：由参数估计结果可知，参数估计值的MC 误差远小于其标准差，这表明该算法是有效可行的；从平均波动水平参数μ 来看，μ 的估计值为0.551 0，其估计值较小，这表明沪深300指数的总体风险是较小的；在波动持续性参数φ 的估计结果方面，其估计值为是0.98，这说明沪深300 股指具有高度的波动持续性；从波动干扰水平σ 来看，其值为0.166 0，这表明隐含波动率的干扰较小；从隐含波动率时序图来看波动幅度在0.45～0.65，意味着其波动较小，风险较小，并且大幅度波动与小幅度波动都存在波动聚集现象.

表4沪深300股指的FMCMC估计结果Tab.4 FMCMC estimated results of Shanghai and Shenzhen 300 stock index

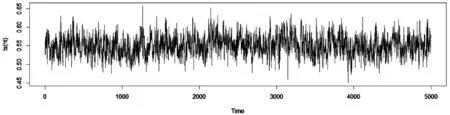
图2 沪深300股指的FMCMC估计波动率时序图Fig.2 Estimated volatility sequence diagram of Shanghai and Shenzhen 300 stock index basing on FMCMC method

沪深300 指数对于指数衍生的创新以及数字化投资具有着十分重要的作用，既是投资业绩情况的评价标准，也是编制目标和运行状况的重要金融指标之一.从模型的参数θ =(μ,φ,σ)′以及波动率序列H=(ht,…,hT)′来看，沪深300指数具有风险较小，波动幅度小，波动率具有持续性的特征，因此，沪深300指数组成股较为适合投资者长持，但由于沪深300指数反映的是A股市场总体状况，因此投资者应该使用合理化的投资组合结构，分散化投资，降低投资风险.另一方面，沪深300 指数除了为市场提供一个投资标尺外，还有一个重要目的是为了股指期货提供一个标准，通过沪深300指数可以推出以该指数为标准的股指期货，为期货交易提供参考依据，因此沪深300指数也可作为投资期货的一种重要手段.实际上在进行金融投资活动时，还会出现的各种影响因素以及不确定风险，例如投资者不可能充分考虑的影响因素、政府对市场的干预、成分股分红等等，尽管沪深300股指在总体上风险较低，波动幅度不大，但投资者应提前做好应对措施，在金融交易的过程中保持谨慎.

4 总结

我们结合了基于Cholesky因子算法的MMP算法以及混合正态算法，提出一种快速的FMCMC算法，通过随机波动率模型的数值模拟研究，研究结果表明FMCMC 算法相对目前流行的Gibbs 算法以及MH算法，能够更加准确以及快速地估计模型参数，通过设置不同参数真实值以及不同长度的模拟时间序列数据，FMCMC 算法均能够较为准确地估计参数值.最后通过实证研究发现，沪深300 股指对数收益率具有尖峰后尾以及波动聚集性等特征，通过波动持续性参数的估计值可知沪深300 股指对数收益率的波动具有较强的持续性，这说明一旦出现较大的波动，有较大的几率会出现由高波动水平持续不降的现象，并且伴随着波动集聚的现象，同时根据其他参数，也说明了沪深300股指波动幅度并不大，其风险也较小，验证了FMCMC算法的有效性.