复杂网络的交通拥塞缓解策略研究

尹荣荣，王 静，刘 蕾，邓玉静，赵 凝

(燕山大学信息科学与工程学院，河北秦皇岛066004)

(燕山大学河北省特种光纤与光纤传感重点实验室，河北秦皇岛066004)

1 引 言

交通是国民经济的基础产业，也是社会发展和人民生活水平提高的基本条件.随着国民经济的快速发展，对交通运输的各种需求明显增长，交通拥塞问题也随之产生［1-3］.交通拥塞问题已经严重明显影响人们的正常生活，降低人们的生活质量，因此解决交通拥塞问题十分重要.

近年来，国内外学者针对交通网络的拥塞问题已经做了许多研究.Jiancheng Long 等［4］利用细胞传输模型，模拟交通阻塞的形成和消散，提出一种应用于事故拥塞的细胞传播模型.在此基础上利用交通阻塞传播的空间拓扑结构，结合车辆禁行的概念，提出了有效的控制策略来分散基于事故的交通拥堵［5］.Liang Qi 等［6］在信号交叉口设计了两层策略，通过增加城市交通警示灯来防止基于事故的城市交通拥堵.Shaohu Tang 等［7］提出了基于城市交通需求的区域划分方法，结合过饱和区域优化控制方法，建立了基于多学科设计优化的子区域信号优化控制及分布式协同控制模型.Gunasekaran Muthumanickam 等［8］提出了一种交通拥堵控制方法，主要探讨了滑动窗与流量密度的关系，以减少交通阻塞控制机制中的时延.Chantong Lam 等［9］利用当地政府提供的在线图像，提出了一种经济的实时城市交通拥堵检测系统.李彦瑾等［10］构建路网的几何拓扑图，依次从拓扑图中删除拥堵节点，建立评价指标衡量路网通行效率，并计算级联失效时的路网拥堵度.孙景昊等［11］基于实时演算理论，针对定时和自适应两类信号控制系统，建立了统一的城市交通网络形式化模型，控制交通拥塞.Zeng Guanwen［12］对大量的城市交通实测数据进行研究，在不同的流量动态下，两种临界渗流行为模式在相同的网络拓扑结构中发生切换，有利于理解和提高交通弹性.Brennand Celso A R L 等［13］通过道路分类和为车辆提供新路线的方法，提出一种用于控制拥塞的流量服务模型.文献［4-13］都是从控制信号灯与减少流量等方面对交通拥塞问题进行研究，为交通拥塞问题的解决作出了贡献.

由于交通网络存在的一个重要特点——时空分布的复杂性［14］，在解决交通拥塞问题时，需要考虑交通网络拓扑具有的结构特征.因此，一些研究学者利用复杂网络理论解决交通拥塞问题.李树彬等［14］运用改进的中观交通流模型，研究了网络拓扑结构对交通拥堵的影响，进而分析复杂网络上的交通传播动力学特征和传播规律.SoléRibalta Albert 等［15］基于复杂网络中出现的拥塞现象，提出了交通网络拥塞的预测模型.该模型能够分析并预测城市环境中的拥堵问题，具有良好的可分析性和可迭代求解性.Shibao Li 等［16］基于复杂网络模型，提出了一种基于交通优先级拥塞控制路由策略，可用于解决不同交通拥塞情况.陈伟哲等［17］基于大型城市道路网络具有无标度分布的性质，提出了一个适用于封闭小区开放问题的城市道路网络模型，提高了城市路网的通行效率.陈晓明等［18］针对城市交通网络中旅客在公共交通出行路径选择时的问题，提出一种基于双层复杂网络的城市交通网络协同优化方法，能够使网络全局效率和旅客换乘行为达到最优.Lishan Sun 等［19］基于复杂网络理论，提出了一种基于耦合映射格的加权级联失效模型，为缓解交通拥塞提供了理论支撑.上述文献运用复杂网络从理论上对交通拥塞问题进行了研究，但是结合交通流入/流出量与行驶过程中随机性不够紧密.

本文将城市交通网络映射为双向网络，定义节点的流入、流出量;将道路关闭的策略引入到网络中，拥塞节点的流入道路从全部关闭逐渐开放，得到拥塞缓解时间，制定拥塞的缓解规则.通过仿真验证拥塞缓解规则中的多个参数对拥塞缓解时间的影响，能够得到此拥塞缓解规则对网络的堵塞有一定缓解的作用.通过扩大整个网络的节点总数，拥塞缓解规则同样适用.

2 负载容量模型

城市交通网络可以看作一种的复杂网络，对于交通网络拥塞问题的研究是将交通网络抽象为双向网络.网络具体的抽象过程为:将路口抽象为节点，基于道路上车辆的行驶规则是按双向车道行驶，即两个相反的方向行驶，由此道路抽象为具有流入/流出的双向的边.那么对于路口拥堵而言，车辆的流入少于流出时，路口不易发生拥塞;而车辆的流入多于流出时，路口易发生拥塞;由于车辆的流动性，流入的车辆在经过路口之后成为流出的车辆，路口流入/流出的车辆都是来自路口连接的道路，故道路上的车流量就是道路(支路)的负载.本文侧重的是路口拥堵之后如何缓解的问题，实际路口具体有几条流入/流出的道路，是针对路口的道路数而言的，由此将路口的道路数抽象为节点的度.

2.1 节点负载

众多研究表明，每个节点上的初始流量与其密切相关［20，21］，因此节点的初始负载定义为与节点度有关的函数，表示如下:

2.2 流入/流出量

设定每个支路(道路)的容量为一定的，单位时间内，i 节点的信息通过某一支路达到邻居节点j.此时，支路上i 节点的流出量也就是j 节点流入量，因此i 节点的支路流出量等于邻居节点j 的支路流入量.每个节点、每个支路之间的流量是不同的，本文认为路径长度越长的支路，单位时间内的流入流出量越大，由此定义支路上单位时间内的流入流出量和支路路径长度成正比的存在，表示如下:

其中，Lin(ij)为节点i 到节点j 支路上每秒的信息流入量，Lout(ij)为节点i 到节点j 支路上每秒的信息流出量，δ 为正比例系数并且δ≥1，Dij表示为节点i 到节点j 的路径长度。

上述可知，若道路全部开通的情况下，节点的度等于节点的流入度，等于节点的流出度。又因为节点的负载和节点的度成比例存在，所以，节点i 的单位时间内的信息流入量为

同理，单位时间内的信息流出量为

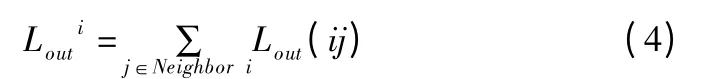
2.3 节点容量

节点容量指的是节点能够容纳负载多少的量值，与节点负载紧密相关.通常情况下，节点的容量定义为与节点初始负载成正比的量［22］，表示如下:

其中，Ci(t)表示为节点的容量，β≥0 是节点容量与节点初始负载的比例参数.

3 拥塞缓解规则

3.1 负载分配规则

交通拥塞发生以后，整个网络需要按照一定的规则进行负载分配，直至拥塞缓解完毕，并且整个网络的节点不再拥塞为止.

3.1.1 传递概率

负载量在信息传递过程中，到达每个节点的可能性不同(即交通行驶过程中的随机性).节点i 的负载，需要通过邻居节点传送到目的节点上，认为节点的度越大，通过该节点的可能性越大，即将从节点i 到节点j 的可能性，设为度的比值:

其中，节点j 是节点i 的邻居节点，εij为传送过程中从节点i到达任一邻居节点j 的可能性。由于节点i 的信息若要流向目的节点，肯定需要通过i 的邻居节点j，其可能性之和符合全概率公式.

3.1.2 最短缓解时间

假设节点i 当前的负载量为Li(t)(Li(t)＞Ci(t))，即该节点发生拥塞，需要将其多余负载向邻居节点进行分配.若节点能正常工作，在仅仅只考虑i 节点自身的缓解能力情况下，节点i 缓解这些多余负载需要用一定的时间，即当=0时，此时节点拥塞缓解时间最短为

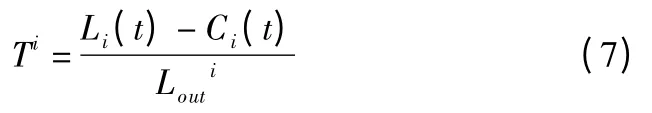
其中，Ti为仅考虑节点的本身的缓解能力下的拥塞缓解时间.

但是在缓解节点拥塞的过程中，需要考虑交通行驶的随机性。将拥塞节点的流入道路全部关闭时，结合公式(6)按照交通中传递的概率εj进行分配代入公式(7)，能够得到考虑交通传递概率时，拥塞缓解节点所需的最短时间，即在流入量为0，节点只向外流出时，节点缓解多余负载所需的时间为:

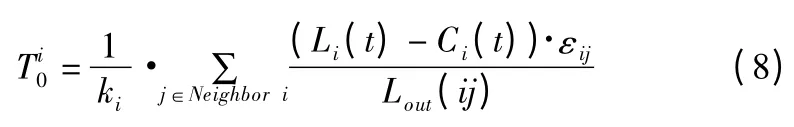
3.1.3 拥塞缓解时间

下面讨论在缓解时间内，邻居节点到拥塞节点的流入量从全部关闭至逐渐开放，由于分配到各个邻居节点的负载不同，开放不同的节点(本文中按邻居节点度从大到小开放道路)，节点拥塞缓解的时间也有所不同，将此思想代入公式(8)，节点拥塞缓解时间定义如下:

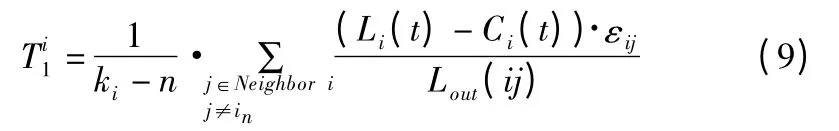
由式(10)能够得到，开放关闭道路个数n 越大，节点拥塞缓解时间越大;路径正比例系数δ、容量比例β、负载强度 τ 越大，越小，其中 δ 与成反比关系.而失效节点的度ki、邻居节点的度kj、路径长度Dij与的关系无法直接从公式中推导出来.

本文重点讨论在道路拥塞的情况下，所有流入道路从关闭至逐渐开通时，开通的关闭道路数n 对拥塞缓解时间的影响.从上述的推导式(10)中可知，δ、τ 为影响拥塞缓解时间的次要影响参数:δ 为支路路径的正比例系数并且δ≥1，对于的影响较小，本文中设δ=1;τ 为控制初始节点负载强度的可调参数，并且τ≥1，本文中设τ=1.β、n 为公式(10)中的主要影响参数:β≥0 是节点容量与节点初始负载的比例参数;n 为开放关闭道路的个数，n≥1.

3.2 拥塞缓解规则

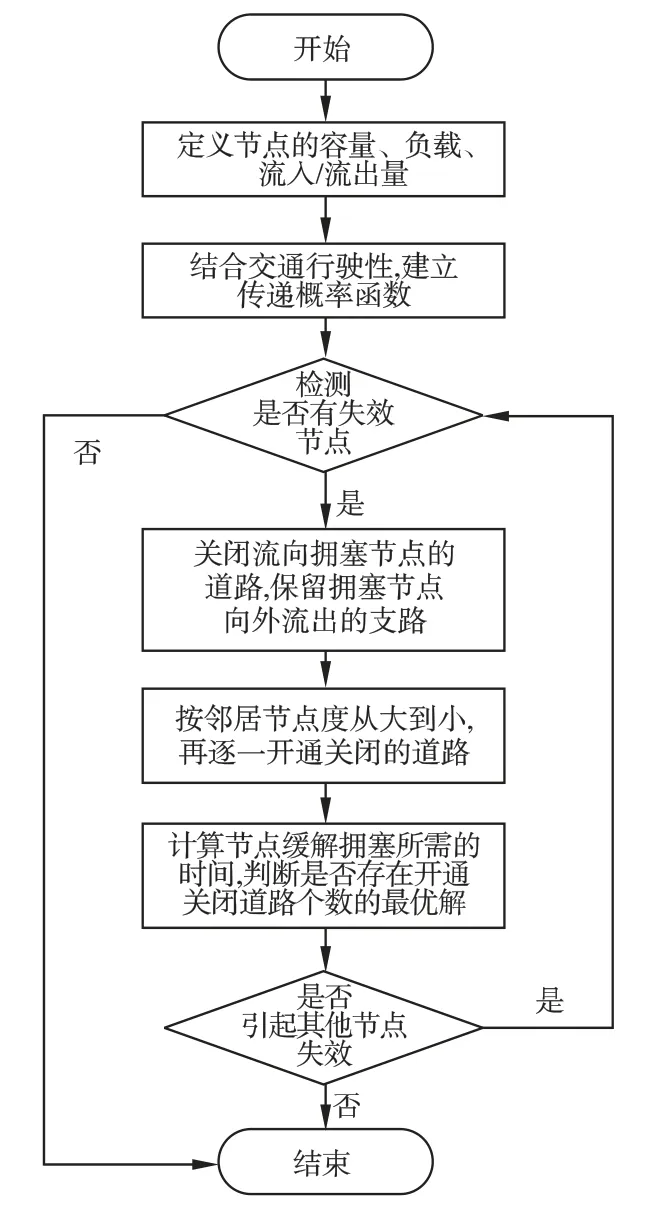
图1 缓解规则流程图Fig.1 Flow chart of mitigation rules

对于拥塞缓解的规则，是将路口关闭的策略引入到网络中.在路口i过载时，将流向节点i的道路从全部关闭至逐渐开放，将节点i 的多余负载按一定规则分配到邻居节点上，计算此时缓解负载所用的时间.整个拥塞缓解的规则，如图1所示.

4 仿真验证

大量的文献表明城市交通网络呈现出复杂网络的特性［23，24］.Wu Jianjun 等［25］对北京市公交网络进行研究，实验结果表明，北京公交网络分布呈幂律分布.Dimitrov Stavri Dimitri 等［26］指出城市交通网络的度分布服从广义的幂律分布，即无标度网络特性.因此，本文仿真在BA 无标度网络基础上进行验证，具体的网络拓扑参数如表1 所示.

表1 实验参数Table 1 Experimental parameters

在上述参数的网络下，将各个参数对拥塞缓解规则的影响分别进行仿真验证.

4.1 容量比例

由式(10)中理论中可以得到，节点容量与节点初始负载的比例参数β 越大，拥塞缓解时间越小，下面仿真验证容量比例β 的变化对拥塞缓解时间的影响，结果如图2 所示.

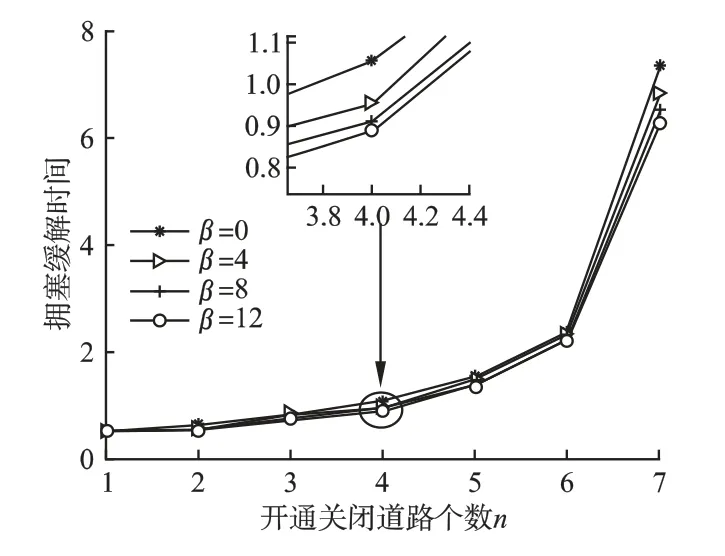
图2 容量比例β 的变化对拥塞缓解时间 的影响Fig.2 Impact of capacity ratio β change on congestion mitigation time

由图2 可以看出，β 由小到大变化时，拥塞缓解时间T1i相应变小，与理论中分析的变化相吻合，β 表示节点的容量比例参数，节点容量越大，缓解拥塞的能力越强，与一般认知相符.由于几条曲线变化规律一致，但是数值较小，表示容量比例β 的变化对拥塞缓解时间的影响较小，对拥塞缓解时间的影响可以忽略不计，因此，本文选取β=1 作为节点容量与节点初始负载的比例参数.

图3 开通关闭道路的个数n 对拥塞缓解时间 的影响Fig.3 Impact of the number of open and closed roads n on congestion mitigation time

4.2 开通关闭道路的个数

从公式(10)中可以看出，开放关闭道路的个数n 对拥塞缓解时间有一定的影响，具体的变化结果如图3 所示:

4.3 失效节点度

从公式(10)中可以看出，除开放关闭道路的个数n 以外，失效节点度的变化对拥塞缓解时间有一定的影响，具体的变化结果如图4 所示.

图4 不同的失效节点度下，拥塞缓解时间的变化Fig.4 Changes in congestion mitigation time under different failure node degrees

从图4 可知，单从一条曲线可以看出，开通关闭道路的个数n 越大，拥塞缓解时间也随之增大，有明显的变化趋势.从多条曲线对比可知，失效节点度ki越大，拥塞缓解时间的拐点越来越明显.

为了更好的分析图4，将图4 局部放大，可得到图5.

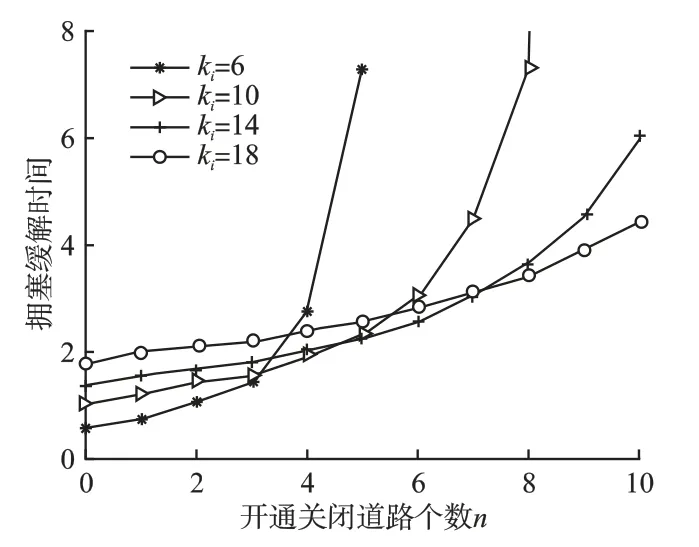
图5 局部放大的不同度下拥塞缓解时间变化Fig.5 Changes of congestion mitigation time under different degrees of local magnification

由图5 所示，在 ki=6、ki=10、ki=14、ki=18 每相邻两曲线都存在重合点(本文称为拐点)，以ki=14 和ki=18 曲线为例，两曲线在n=7 时重合，在该拐点以前，相同的开通关闭道路个数n 下，失效节点度ki越大，拥塞缓解时间越大;在拐点之后，失效节点度ki越大，拥塞缓解时间越小.但是，对于一条曲线在拐点之后，随着开通关闭道路个数n 越大，拥塞缓解时间迅速变化.进一步可知，ki=6、ki=8、ki=10 的相邻曲线分别在n=3、n=4 处重合，变化规律同上.由上述规律可得，一般拐点存在于处，对应的拥塞缓解时间都比较小.由此，为保证路口能够获得较短的拥塞缓解时间，开通关闭道路个数应为.

4.4 节点总数

上述仿真验证都是在节点总数一定的情况下，但是仿真环境中的节点总数N 变化对拥塞缓解时间的影响，需要进一步仿真验证.因此，本文在仿真区域一定的情况下，以失效节点度ki=10 为例，将节点总数N 变化对拥塞缓解时间的影响进行验证如图6 所示.

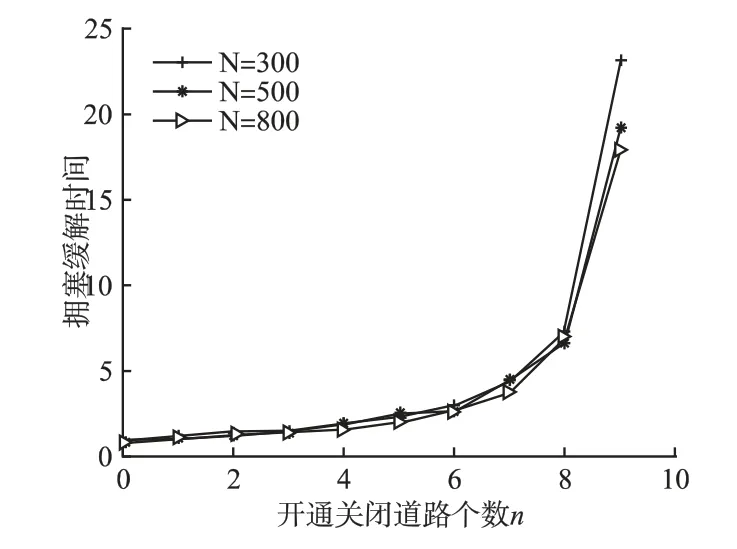
图6 节点总数N 变化对拥塞缓解时间的影响Fig.6 Impact of total number of nodes N on congestion mitigation time

由图6 所示，节点总数 N=300，N=500，N=800 对拥塞缓解时间的影响三条曲线几乎重叠，因此，节点总数N 变化对拥塞缓解时间几乎没有影响.由此可知，本文中的拥塞缓解规则对节点疏密分布的区域都可适用.

4.5 仿真小结

上述仿真的结果符合人们平时的认知，关闭拥塞节点的流入量，能够对节点拥塞起到缓解作用.通常情况下，在交通网络中可以通过控制红绿灯的时间配合拥塞的缓解，拥塞缓解时间对应的是红绿灯的时长，延长邻居节点红绿灯的时长，拥塞节点的交通流入量可以得到控制.当流入方向的道路全部关闭时，拥塞缓解所用时间最短，随着道路逐渐开通，拥塞缓解时间相应增加，为保证路口能够较快的缓解拥塞，开通关闭道路个数可设定为.

另一方面，将一个节点的堵塞分散到了多点邻居节点上，单个节点需要分担的流量会相对减少，可以将拥塞控制在一定时间内，不会造成长时间拥堵.当然，从网络层面来讲，这个过程是一个级联失效的过程，如何减少整个交通网络级联失效的程度和网络拥塞时间的影响是我们接下来要做的工作.

5 结 论

针对城市交通网络的拥塞问题，本文基于关闭道路的思想，考虑交通的特点，建立了一种基于复杂网络的拥塞缓解规则.关闭其他节点流入拥塞节点的负载量，拥塞节点的流出量不变，将一个节点的堵塞分散到了多点邻居节点上，每个节点需要分担缓解的负载量会相对减少.仿真分析可知，该拥塞缓解规则不仅能够减小交通拥塞的缓解时间，可以将拥塞一定程度内控制在一定时间内，而且适用的网络规模比较广泛.