基于DAE的工控系统态势理解算法

尚文利，敖建松，赵剑明，刘贤达，尹 隆

(中国科学院沈阳自动化研究所，沈阳110016)

(中国科学院机器人与智能制造创新研究院，沈阳110016)

(中科院网络化控制系统重点实验室，沈阳110016)

(中国科学院大学，北京100049)

1 引 言

态势感知(Situation awareness)是一种从宏观的角度上去理解系统现状，判断是否遭受攻击，并预测系统未来发展趋势，从而提前做好防护动作，阻止系统态势进一步恶化的手段［1］.其概念起源于军事对抗研究，其目的是结合敌我双方的现状，以及战场上的各种实时因素，预判敌人的下一动作.Endsley［2-4］将其归纳总结为三个阶段:态势要素获取，态势理解，态势预测.Bass［5］结合态势感知概念，发现传统安全检测手段的局限性，提出网络安全态势感知(NSSA)，和应用于多传感器数据融合的网络空间态势感知框架;文志诚等［6］通过构造隐马尔可夫模型，利用时间序列分析方法刻画不同时刻安全态势的前后依赖关系，当安全态势偏离正常时，启动态势预测的机制，预测系统未来态势.Fava 等［7］提出了通过IDS 的报警记录来建立词缀树，并且通过词缀树来训练出长度可变的马尔可夫模型(VLMM)，进而预测出攻击者的下一步攻击.

为了更好的应对越来越多的工控系统网络安全挑战，对工控系统安全态势感知技术的研究也逐渐开始.Evesti 等［8］借助态势感知实现工控系统的自适应安全，辅助系统管理人员制定安全决策;曾伟兵等［9］结合当前工业控制系统的特点，提出一种基于多Agent 协同处理技术设计开发了恶意代码行为捕获原型系统并利用一种改进的模型算法，能实现对系统中的恶意节点快速定位;Hoffman B 等［10］通过分析震网病毒案例，把整个对工控系统的攻击过程抽象成含有6 个攻击阶段的态势链，通过对系统中各个节点的报警信息融合处理，理解系统当前处于某个阶段，便可通过态势链预测系统下一个即将到达的攻击阶段，提前对系统进行相应的安全防护.虽取得一系列初步的成果，但目前工控系统安全态势感知技术大多仍停留在理论研究阶段，主要原因在于:其一目前针对工控系统的信息安全需求以及技术研究尚不成熟，其二，在工控系统网络安全领域缺少足够的数据支撑.

本文结合工控系统的实际运行特点，考虑当前大多数工控系统网络入侵的最终目的就是通过网络层的入侵实现对控制指令的篡改，使现场控制层某些变量数据发生异常变化，从而对整个系统造成实质的破坏，所以工控系统现场控制层安全状况很大程度上表征了整个系统的安全状况.由于现代工业控制系统多为非线性复杂控制系统，其现场控制层数据通常具有维度高、数据量大，且不同节点的数据之间存在着非线性相关关系的特点，而态势感知的最终目的是实现实时的把控系统安全，并对系统未来的运行状况实现精确预测，无论是从实时性还是模型的精确性的角度来讲，都需要对原始数据实现降维，压缩数据空间，过滤掉冗余信息，提炼出有用的数据信息.

本文通过深度学习中的去噪自编码器来对原始数据进行处理，提炼出有效的安全态势要素作为后续态势理解算法的输入，再利用K-means 等聚类算法实现系统正常状态空间建模，通过实时检测的数据，度量出实时状态的偏离程度，最后利用长度为L 的滑动窗口来基于时间维度上的融合计算，得到实时系统的态势，为后续态势预测提供合理有效的输入.

2 态势要素提取方法

工业控制系统易受到各种恶意攻击［11］，文献［11］给出了详细的阐述，其中不法黑客常见的攻击手段为恶意数据注入攻击［12］，其目的是为了恶意的篡改工控系统的控制现场层中的某些参数变量，从而使其偏离正常运行状态，对系统造成破坏.

而在态势感知模型研究中，最基础也是最重要的一层是态势要素提取层，结合被恶意数据注入攻击的系统的数据行为特点，通常需要对系统中各个位置节点的数据信息进行归纳总结［13］，去除掉冗余和无效的数据信息，保留下可以表征系统态势的有效数据信息.而对工控系统而言，其控制现场层的各个位置存在大量的传感器节点，所采集的数据为多变量大数据集，多变量数据提供了丰富的数据信息，但是一定程度上增加了数据采集和存储的成本;作为非线性复杂控制系统，各个节点之间很大概率存在着强烈的非线性相关性，若直接作为输入进行后续的模型建立，会导致模型复杂度过高，泛化性偏低，直接影响整个态势感知模型输出的可靠性，而直接对单个节点的数据进行分析剔除又不能完全利用数据中蕴含的信息，导致损失过多的有效信息，所以需要用到机器学习或者深度学习领域中的降维算法来实现从原始规模的数据中精炼出有效的数据信息，在减少数据维度的同时，最大化的保留有效的数据信息.

2.1 主成分分析(PCA)

PCA，即主成分分析方法，是机器学习领域中被广泛使用的一种线性降维算法，其核心思想是把M 维数据通过线性变换，转换为N 维数据，其中M＞N，从而达到一个压缩原始数据空间的效果，使后续的模型或者算法在计算速度更快，消除了原有特征之间的相关度，减少数据信息的冗余，提高模型的精度［14，15］.

具体算法步骤如下:

Step 1.对每个维度进行去除平均值:

Step 2.计算协方差矩阵:

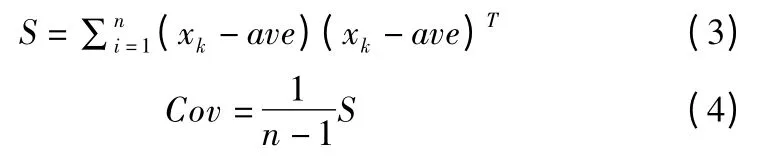
Step 3.计算协方差矩阵的特征值和对应的特征向量;

Step 4.将特征值从大到小排序;

Step 5.保留上面对应的N 个特征向量，组成矩阵P;

Step 6.将数据转到上述N 个特征向量构建的空间中:

得到降到N 维后的数据.

该算法对数据量较少且数据特征之间仅仅存在线性相关性的数据集具有很好的降维效果，但是在对工控系统现场控制层的数据进行处理时该算法的局限性就被放大了，这是因为现实中工控系统运行过程中所采集数据量大，且各节点之间存在着未知的非线性相关性.

2.2 去噪自编码器(DAE)

自编码器(AE)是一种神经网络，也是一种无监督学习算法，它可以使用自身的高阶特征来编码自己，它的基本思想是通过设置隐藏层的神经元个数来决定数据变换之后的维度，同时通过隐藏层的输出重构自己，使最后整个网络的输入和输出一致，多用于数据的压缩降维，见图1.它相比于PCA等降维方法而言非线性泛化性更好，它既能表征线性变换又能表征非线性变换［16］.

图1 自编码器Fig.1 Autoencoder

自编码器的整个过程可以由下式表示:

h 代表整个编码解码过程，W 和b 是需要通过数据训练出的参数，隐藏层的输出就是数据通过自编码器降维之后的结果，再把隐藏层的输出进行重构，使整个自编码器的输出x'最大的逼近输入x，式(4)是该训练过程的损失函数:

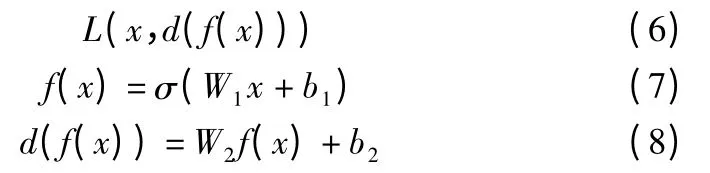
损失函数度量了x'与x 的差异，式(5)代表编码过程，也代表隐藏层输出;式(6)是解码过程，对隐藏层的输出进行重构得到x';W1，b1和W2，b2分别是通过数据训练得到的编码和解码过程的权值和偏差，σ()为非线性激励函数，通常也叫神经元的激活函数，本文使用的是sigmoid 函数:

整个训练过程可以通俗的描述为不断的调整W1，b1和W2，b2，取使损失函数达到最小时候的 W1，b1作为最终数据降维的参数.

自编码器(AE)现在广泛运用于数据降维以及自动特征提取领域.文献［17］中以自编码器为理论基础，对KDD99 等相关数据集实现自动特征的提取，最后结合随机森林等浅学习方法，实现对攻击数据的高精度的检测，该方式不仅降低了数据维度，减少了后续分类模型的计算消耗和提高了模型的精确性;文献［18］提出一种稀疏去噪自编码器的入侵检测方法，该方法针对传统浅层的入侵检测方法无法有效解决高维网络入侵数据的问题，利用改进的稀疏去噪自编码器对数据进行降维，最后利用softmax 分类器进行检测，实验结果证明，该方法提高了将近5%的准确率.

上述研究成果表明自编码对高维数据进行适当的处理降维后能大幅提高后续建立的模型性能.而本文根据工控系统现场控制层的数据特点，采用去噪自编码器来对数据进行降维处理，去噪自编码器(DAE)是基于传统自编码器的理论基础改进得到的一种神经网络［19，20］，基本结构与图2 基本一致，它与传统自编码器的区别在于对训练数据按照规定的分布加入适量的随机噪声，输出标签仍然是原来的样本，进行训练，使其训练出来的模型更具有鲁棒性，可以提取出更好的数据信息.

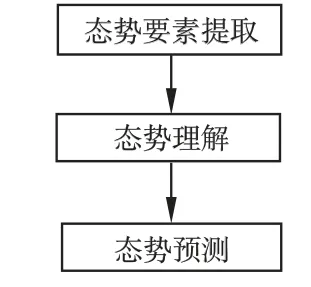
图2 工业控制系统态势感知流程图Fig.2 Situation awareness model of industrial control system

3 聚类算法

聚类算法是一种无监督学习的算法，它的主要作用就是把一个数据集划分成多个类;在回归、分类等有监督学习任务中要定义输入数据的类别标签，以此来训练出对应的模型;但是聚类算法的输入数据没有类别标签，所以适用于许多难以获取带标签数据的应用［21-25］，在本文中主要被用于进行工控系统现场控制层的正常状态空间的建模工作.

聚类算法的核心思想是基于数据之间的相似性来对其进行分类，所以不同的聚类算法具有不同的相似度定义.尽管现在已经存在多种聚类算法，但是'最好'的聚类算法还是依赖具体的应用场景和输入对象的类型格式等，针对本文使用的实验数据集而言，使用K-means 来构建的态势理解算法的输出已经满足预期的效果.

K-means 算法是聚类算法中比较简单的迭代型聚类算法，实现简单，速度快，便于理解和修改，是现实中使用最广泛的一种聚类算法，该算法中，每一个聚出来的类用一个点Xn来代表，n 是代表数据的维度，这个点也被称为聚类中心，而最终会有多少个聚类中心是输入的时候人为设定的，也就是k 值，它决定了输入的数据聚类的类别数量.这些聚类中心可以用一个集合表示K-means算法的相似度是默认用欧几里得距离来度量，训练过程是通过对聚类中心的更新迭代最小化如下的代价函数:

具体算法步骤如下:

Step 1.确定 k 值;

Step 2.从输入的数据集D 中随机挑选k 个数据点，构成初始的聚类中心集合C;

Step 3.依次计算数据集D 中每个数据点与集合C 中各个聚类中心的欧几里得距离，把该数据点分配给距离最小的聚类中心;这一步会对所有的数据点都指定一个聚类中心;

Step 4.更新聚类中心，计算所有分配给该聚类中心的数据点的中心，比如算数平均数，得到该类新的聚类中心;

Step 5.重复 Step 3 和 Step 4，直至 Loss 最小化收敛.

K-means 算法对初始聚类中心集和k 值非常敏感，换句话说，能否把真正属于同一类的数据点聚到一起很大程度上取决于初始聚类中心的挑选和k 值的大小.有很多办法针对上诉的问题，防止K-means 局部收敛，以及一些关于聚类中心初始化问题［26-28］，本文使用多次随机抽取聚类中心和k 值来运行算法，然后挑选出最好的结果.

4 工控系统态势理解算法

整个工控系统态势感知模型主要分为3 个阶段:态势要素提取，态势理解，态势预测;每一个阶段都依赖上一个阶段的输出.

其中态势要素提取层作为基础层也是最重要的一层，它的作用是从系统中提取出一些能够表征系统状态的信息也叫做安全态势要素，本文使用去噪自编码器去掉冗余无效的信息实现自动的提取有效的态势要素，把这些信息作为态势理解层的输入;态势理解层对输入进来的信息做融合分析处理，得到系统当前安全态势;而态势预测层就根据系统当前的态势来预测系统未来时间的态势，配合安全管理人员做出正确的防护决策.

态势理解算法主要是为了直观的呈现出系统实时的安全状况，从工控系统现场控制层数据中提取出有效的态势要素，并进行合理的融合，实现当前态势理解.

本文提出的工控系统态势理解算法流程如图3 所示，具体步骤如下:

Step 1.在历史数据库中取出系统正常运行时段的现场控制层所收集的数据;

Step 2.利用去噪自编码器对数据进行压缩降维，得到过滤掉冗余信息，保留主要信息的数据，并保留模型参数，以便后续实时检测阶段中对输入的样本进行态势要素提取;

图3 基于DAE 的工控系统态势理解算法流程图Fig.3 Flow chart of situation understanding algorithm for industrial control system

Step 3.对经过Step 2 变换之后的数据进行K-means 聚类，得到k 个聚类中心，和对应的k 个类别的数据集，对应k个正常运行工况;

Step 4.计算每个类别的数据集中每个数据点到对应的聚类中心的距离，取出最大值，记 dismax，得到集合 Dis=;

Step 5.对每个实时检测到的数据做同样的降维处理操作，并且计算到每个聚类中心的距离，得到Dis_t={dis_tj|j=1，2，3…k}，再计算 d=Dis_t－Dis，得到 d={dj=(dis_tj－};

Step 6.如果Adj∈d＞0，则记该时刻系统状态偏离系统正常工况的程度为ε=min (d)，否则记ε=0.

Step 7.以长度为L 的滑动窗口，在时间维度上对ε 进行融合，统计得到该时刻 ε 的均值 εavg和方差 εs;均值反应了系统在当前时刻系统偏离正常工况的程度，方差体现了系统状态的稳定性，最终得到表征系统态势的二元组S=(εavg，εs).

5 实验与数据分析

由于目前在工控安全领域还没有一个标准的测试数据集，尤其是实际工控系统在攻击下的数据更是难以获取，结合参考文献［12］的实验思路，以及在攻击情况下，工业控制系统现场控制层的数据变化情况，所以本文使用了比较符合研究场景的Tenessee Eastman(TE)化工仿真数据集作为验证数据集来说明算法的可执行性和有效性.整个数据集由训练集和测试集构成，包括正常状态的数据和不同类型的异常状态数据，不同类型的异常数据样本中有960 个状态数据，仿真时在第160 个时刻时引入异常，所以前160 个数据为正常数据，本文随机取出4 个异常状态数据样本作为测试集进行实验验证，以异常工况1 和2 的数据样本组成测试集1，异常工况3，4的数据样本组成测试集2，在测试集中数据分布为:［1，160］，［961，1120］时刻对应的数据为正常状态数据，其他时刻区间内为异常状态数据.

5.1 态势要素提取

该数据集有52 个维度，表征系统运行时现场控制层中的各个传感节点所检测的数据，例如同一时刻不同节点所检测的温度，压力等.该仿真系统属于非线性复杂控制系统，有许多维度之间存在未知的非线性相关性，不利于后续要素融合计算处理，影响最终模型精度，所以需要使用去噪自编码器进行数据变换，自动提取有效的数据信息，在保证最小化损失的前提下选择变换之后的数据为42 维.

5.2 实验验证与分析

使用训练集中1000 个正常状态数据来对系统正常状态空间进行建模.在进行K-means 算法聚类的时候，不断的调整k 值，最终取k=5 时，聚类效果最好.而在现实的工控系统运行中，几乎正常工况的个数是有一个确定值的，所以k 的取值可以根据不同的系统以及相关专业人员的知识确定，也可以使用轮廓系数法确定，达到最好的聚类效果.

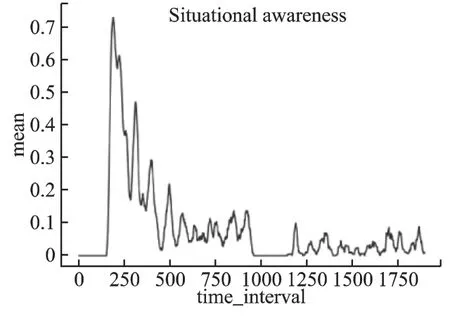
图4 测试集1 中各时刻εavgFig.4 εavg at each time in test set 1

最后以四个异常状态数据样本作为测试集，整个算法输出各个时刻系统实时状态偏离正常状态空间的程度εavg和稳定性大小εs如图4 所示.

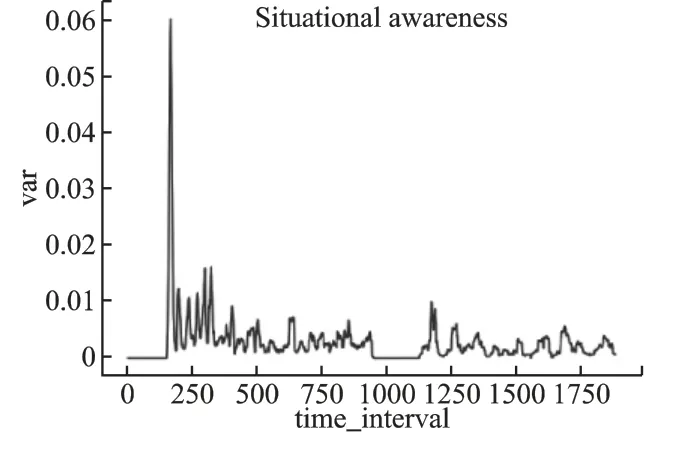
图5 测试集1 中各时刻εsFig.5 εsat each time in test set 1

由图4-图7 可得，由本文所提算法输出的结果与测试集中数据分布几乎一致，即:在系统正常运行时段内，由算法输出的εavg和εs为0 或者近乎为0，而在系统异常运行时段内，所对应时刻的εavg和εs都几乎大于0.

图6 测试集2 中各时刻εavgFig.6 εavgat each time in test set 2

图7 测试集2 中各时刻εsFig.7 εsat each time in test set 2

由表1 和表2 可得，本文所提算法可以在对数据实现压缩降低算法复杂度的前提下，仍然可以很好的把异常状态数据和正常状态数据区别开来.例如在表1 中，在t=80 或t=965 等系统安全运行的时段内，S=(0，0)，表明系统在这些时刻正常运行，而在其他时刻诸如t=180 或t=750 等时刻，S中两个元素均大于0，说明系统在这些时刻运行状态异常，并且在系统状态异常情况下，通过S 中两个元素的数值大小来直观的呈现出系统危险程度，就表1 中t=180 和t=750 两个时刻而言，通过对 εavg和 εs两个值的比较:St=180(0.72，0.060)＞St=750(0.068，0.002)，说明系统状态在 t=180 时刻偏离正常状态空间程度更大，其稳定性更差，整个系统的态势更加危险.由表3 分析可得，在使用去噪自编吗器进行数据空间压缩的前提下，该算法的时间复杂度大大的减少，但是另一方面可以发现其检测精度有略微的下降，这是因为该数据集维度和数量对比现实中系统产生的数据来说还是太小，数据信息的冗余程度过于理想，导致数据降维损失了部分信息，但即使这样，相比于时间成本的降低，其精度损失在大多数场景下也可以被接受，这也为该算法在实际处理大量高维数据的场景中保证检测的实时性和精确性提供了可能性.

表1 测试集1 部分时刻对应检测结果Table 1 Test set 1 partial time corresponding test results

表2 测试集2 部分时刻对应检测结果Table 2 Test set 2 partial time corresponding test results

表3 算法运行结果对比Table 3 Comparisons of algorithm running results

结合文献［12］和上述相关分析可知，被潜伏性恶意数据攻击的工控系统其现场控制层所产生的数据会缓慢的并且有规律可循偏离系统状态空间，从而使后续态势预测阶段可以基于态势理解算法的输出作时间序列上的预测，估计出系统未来时刻的整体安全态势走向，提前作出安全防护决策.

6 结 论

本文提出了一种基于DAE 的工控系统态势理解算法.该算法针对工控系统现场控制层的数据量大，维度高，且存在大量未知的非线性相关性的特点，利用去噪自编码器提取出可以表征系统态势的数据信息(态势要素)并作为后续结合K-means 所构建的态势理解算法的输入，最终在满足算法检测精度的同时，由于数据维度的降低，实现了时间复杂度的降低;最后实验证明本文提出的算法能在检测到系统异常状态的基础上实现对系统安全状况的直观呈现，量化之后的态势能为系统管理人员提供可靠的决策信息，也为后续态势预测研究提供有效的输入.

工控系统态势感知研究领域目前尚处于起步阶段，本文为态势感知研究提供了一种新思路，但是在态势感知的工控独特要求及针对性方法设计方面还有待完善，仍需要更多的探索.