基于两阶段排放算法的矩形件排样优化方法

许继影 陈仕军 郑晴

摘  要： 针对矩形件排样问题，经典的最下左填充（BLF）算法易于出现区域浪费、原材料利用率低的缺点。对此，提出一种改进的两阶段排放算法。第一阶段利用BLF算法，第二阶段设计一个改进BLF排放算法以减小区域的浪费。再以矩形件排放顺序进行编码，利用两阶段排放算法解码，设计邻域搜索算法寻找最优解。通过已有文献的多个案例，对改进的算法进行实验验证，结果与BLF算法相比，原材料利用率能提高14%，证实了改进算法的有效性。

关键词： 矩形排样; 排放算法; 两阶段; 邻域搜索

Abstract： For the rectangle packing problems， the classical bottom-left fill （BLF） algorithm may give rise to the disadvantages of waste area and low utilization of raw materials. Accordingly， an improved packing algorithm with two-stage layout is presented. At the first stage， BLF algorithm is used to pack rectangular pieces. At the second stage， an altered BLF algorithm is presented to fill the left-top corner of the big rectangle. Then the rectangular pieces are encoded in the sequence of placing， the proposed two-stage packing algorithm is used for decoding， and a neighborhood search algorithm is designed to find the optimal solution. Through several cases in the existing literature， the improved algorithm is experimentally verified， and the results show that the utilization rate of raw material can be increased by 14%， by comparing with the BLF algorithm. It confirms the effectiveness of the improved algorithm.

0 引言

矩形件排样问题（也称下料问题）广泛存在于玻璃切割、板材加工、布料裁剪等生产领域，对排样或下料方案进行优化，是企业实现降低成本、提高材料利用率的重要途径。传统的人工制定排样方案会耗费大量的人力和物力，而且材料利用率不高。因此，研究如何采用运筹和最优化方法，并辅助于计算机设备对排样方案进行优化，以提高排样方案的材料利用率，极具重要价值。

矩形件排样问题是计算领域的NP难问题，目前不存在求最优解的多项式时间算法。经典的数学规划方法复杂性太高，难以求解大规模问题。针对该问题，有些学者陆续提出一些求近似最优解的快速排放算法，例如Baker等人提出了最下左（bottom-left，BL）算法[1]，具有复杂度低易于实现的优点。但由于BL算法易产生过多的“空白区域”，考虑到排放利用率低的问题，Hopper与Turton提出一种能填充“空白区域”的最下最左填充（bottom-left-filling，BLF）[2]排放算法;贾志欣提出了一种最低水平线排放算法[3]。同时，BLF算法或最低水平线算法在应用时，矩形件的排放顺序对排样效果影响较大，依靠直观经验或随机选取排放顺序，但往往难以得到理想的排样效果。为此，一些智能优化算法如模拟退火算法、遗传算法、邻域搜索算法等被用于求解矩形件排样问题在内的各种优化问题[4]。Hopper与Turton[2]采用BLF排放算法和遗传算法相结合，求解矩形件排样问题。夏以冲等[5]提出遗传算法和模拟退火算法相结合的方法;郑明月[6]也采用遗传算法和模拟退火算法相结合的方法，但采用了不同的融合策略;也有学者针对特定的下料场景，提出一些特定的下料方法[7-10]。虽然这些排放方法在一些特定排样问题上取得了不错的效果，但方法通用性不够强，计算效率和排样率仍然有较大的改进空间。

传统的BLF算法[2]属于经典的矩形排样算法，具有复杂度低和易于实现的优点，应用较为广泛。但BLF算法易出现大矩形左上方区域浪费的情况，因此提出一种改进的两阶段排放算法，并结合邻域搜索算法，设计出新的矩形件排放算法。对文献中的多个案例进行计算，对所提的改进算法进行实验分析与比较，以验证所提算法的有效性。

1 问题描述与数学模型

记大矩形原料板材的宽为W，高为H，以（W，H）表示;可排放的n个小矩形件分别为R1，R2，…，Rn。矩形件Ri的宽为wi，高为hi，以（wi，hi）（i=1，2，…，m）表示，所有小矩形件的面积之和大于大矩形件总面积，即。对于大矩形件板材，设置其左下角坐标为（0，0）;对于第i个小矩形件Ri，设其排放后的左下角坐标为（xi1，yi1），右上角坐标为（xi2，yi2），其排放前（没选择排放）的右上坐标为（0，0）。若矩形件Ri已排放至大矩形件，记zi=1;否则，zi=0。设M是充分大的正数，则矩形件排样问题可表述成如下的整数规划模型：

上述模型中，公式⑴为优化目标，即最大化排样率;约束⑵与⑶说明小矩形件在板材上，其左下角坐标与右上角坐标的位置关系;约束⑷至⑻，保证板材上任意两个排放的小矩形件互不重叠;约束⑼与⑽保证排放的矩形件不超過板材的边界;约束⑿说明矩形件左下角和右上角排放位置的横坐标与综坐标均在整数位置，约束⑿表示是否排放矩形件Ri。

2 改进的两阶段排放算法

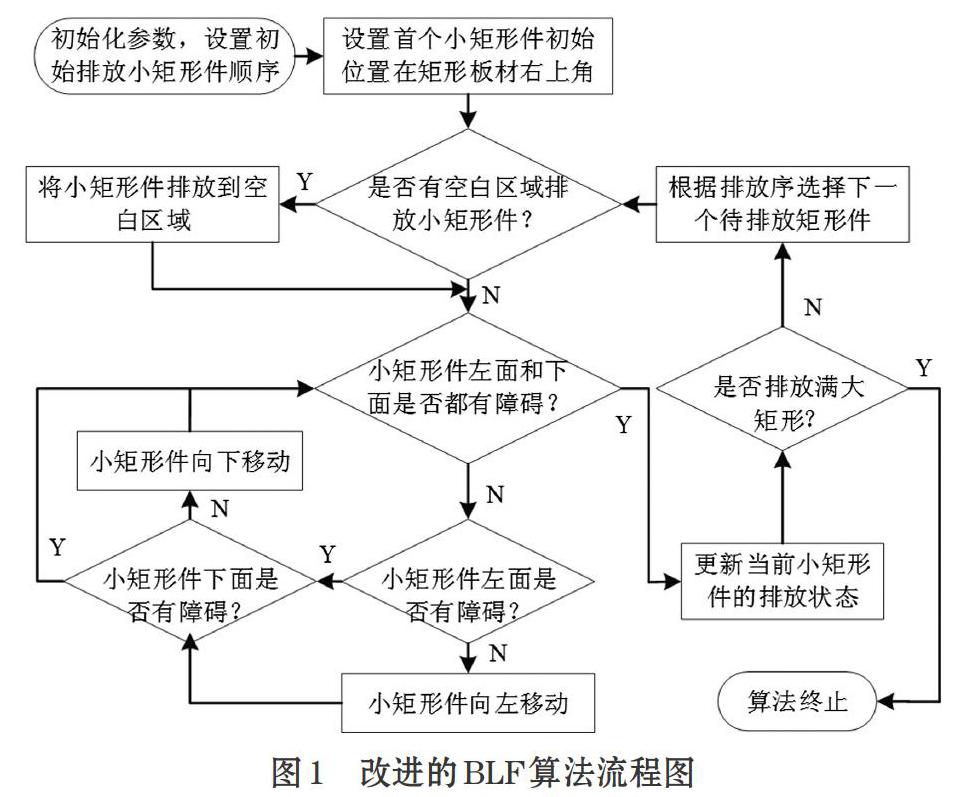
传统的BLF算法[2]步骤如下：先将小矩形件按某种规则（如按面积从大到小）排好顺序;再依次排放小矩形件，优先排放到已放置矩形件的空隙（浪费）区域，如果无法排放，再采用先向下、再向左循环移动，直到小矩形件无法移动为止。该算法每次考虑优先向下排放、再考虑向左排放，容易出现大矩形左上方浪费区域过大的问题。为此，提出一种改进的BLF算法，主要采取优先向左移动、再考虑向下移动，其算法流程如图1所示。

改进的BLF算法克服了大矩形左上方易出现浪费区域的情形，但直接用该方法也会导致大矩形右下方出现浪费区域的现象。为此，设计一个两阶段排放算法：第一阶段，利用传统的BLF算法进行排放;第二阶段，针对可能出现的左上方浪费区域，利用改进的BLF算法排放剩余的小矩形件。

3 基于两阶段排放算法和邻域搜索相结合的排样优化算法

利用两阶段排放算法时，矩形件的排放顺序对最终的排样效果（排样率）有很大影响，因此需要找到最优的矩形件排放顺序。基于两点交换的邻域搜索算法是一种常用优化算法，其算法复杂度低并且求解效率高。为此，先将所有小矩形件进行编码（即小矩形件序号的排列），形成排放顺序，再利用两阶段排放算法进行解码。根据经验可知，面积大的矩形件优先排放时，通常会取得更好效果。初始时，将所有小矩形件按面积从大到小排序，形成初始编码。邻域搜索算子采用两点交换，即随机交换编码中两个小矩形件的位置，保证了搜索解的多样性。当两点交换后，若不能改进当前最优解，则将这两点继续交换，即保持原编码顺序。基于邻域搜索的矩形件排样优化算法如图2所示。

4 案例计算

采用Hopper和Turton给出的12组公开案例[2]，进行实验计算。实验过程中，以最终排样率为指标，分别测试传统BLF算法、改进的两阶段排放算法、基于邻域搜索的排样算法。在利用邻域搜索算法时，迭代1000次寻找最优解。针对每个案例，运行10次邻域搜索算法，并取10次中的最优解。最终计算的排样率结果见表1。

表1中，第2列和第3列分别表示大矩形板材的尺寸和小矩形件的数量。通过表1的第4列至第6列可以看出，改进的两阶段排放算法与传统的BLF算法相比较，前者的平均排样率能提高8.8%。其中案例2和案例4，其排样率没有得到改进，是因为应用两阶段排放算法时，第一阶段左上方没有出现大的浪费区域。通过表1的第7列，可以看出在应用邻域搜索算法后，平均排样率达到了94.54%，相对于传统的BLF算法提高了14.17%。因此，邻域搜索算法表现出较强的全局寻优能力。

5 结束语

在求解矩形件排样问题时，经典的BLF算法易出现左上方区域浪费的情况，本文提出了改进的两阶段排放算法，提高了排样率。再将所提的两阶段排放算法与邻域搜索算法相结合，设计出了更加高效的矩形件排样优化算法，通过文献中的一些案例验证了算法的有效性。此外，如何进一步分析排样问题的本质并提取有用的问题特征，以及基于此设计更高效的邻域搜索算子，还需要进一步深入研究。

参考文献（References）：

[1] Baker B S， Coffman E G， Rivest R L. Orthogonal Packingsin Two Dimensions[J]. SIAM Journal on Computing，1980.9（4）：846-855

[2] Hopper E， Turton B C H. An empirical investigation of meta-heuristic and heuristic algorithms for a 2D packing problem[J]. European Journal of Operational Research，2001.128（1）：34-57

[3] 贾志欣，殷国富，罗阳，徐雷.矩形件排样的模拟退火算法求解[J].四川大学学报（工程科学版），2001.33（5）：35-38

[4] Jain L， Singh G. A review meta-heuristic approaches forsolving rectangle packing problem[J]. International Journal of Computer Engineering and Technology，2013.4（2）：410-424

[5] 夏以冲，陈秋莲，宋仁坤. 基于自适应遗传模拟退火算法的矩形件排样[J].计算机工程与应用，2018.54（22）：229-232，245

[6] 郑明月.混合遗传算法在矩形件带排样问题中的应用[D].合肥工业大学，2013.

[7] 扈少华，潘立武.矩形件五级剪切排样方式的一种生成算法[J].锻压技术，2018.43（10）：190-194

[8] 朱强，薛峰，郑仕勇，管卫利.约束二维排样问题的一种求解算法[J].锻压技术，2016.41（9）：148-152

[9] 沈萍，邓国斌.矩形件剪切下料问题的一种顺序价值修正算法[J].锻压技术，2018.43（4）：180-184

[10] 扈少华，武書彦，潘立武.基于两段排样方式的矩形件优化下料算法[J].图学学报，2018.39（1）：91-96