薄带冷连轧工作辊窜辊边降调控功效

王晓晨，冯夏维，徐 冬，杨 荃，孙蓟泉

1) 北京科技大学工程技术研究院，北京 100083 2) 北京科技大学国家板带生产先进装备工程技术研究中心，北京 100083 3) 机械工业仪器仪表综合技术经济研究所，北京 100055

硅钢叠片常见于电机铁芯，是一种要求极高叠片率的功能性产品.由于宽板轧制时的边降现象，会降低硅钢叠片率及增加层间涡流损失.需要在全连续5机架六辊轧机轧制硅钢薄带过程中，新加入锥形工作辊窜辊功能，从而减小边降、改善叠片率[1−2].因此需要研究新加入的窜辊功能对边降的调控功效.对于宽厚比超过500∶1的宽板轧制过程，对其进行有限元方法仿真计算时间过长，多为单机架模拟[3].但是可以利用有限元揭示某一物理现象，提高解析模型精度.例如，Lee等[4]通过有限元方法研究了热连轧轧后屈服现象，揭示了机架间金属流动减小了带钢同板差，并对解析模型进行了补充，同生产数据比较，提高了解析模型的精度.本文利用有限元方法的横向流动理论，提高Pawelski解析模型[5−6]计算精度，并加入机架间轧后屈服模型，实现两个机架连续计算.通过工业现场实验验证模型精度，经讨论分析提出窜辊边降调控功效系数，以期为工业实践提供理论依据.

1 工作辊窜辊边降调控功效系数

带钢边降的产生是由于带钢在边部的三维横向流动、工作辊弹性压扁、辊系弯矩和机架间变形共同造成的.然而三维横向流动为带钢的固有属性[7−8]，因此只能通过控制锥形工作辊轴向窜动，以补偿工作辊弹性压扁，从而实现对带钢边降的自动控制.目前边降自动控制系统，都是测量末机架出口带钢边部1个特征点附近（距边部15～40 mm）的边降值作为控制依据，然后乘以调控功效系数，得到上游三个机架的工作辊窜辊增量.然而实际工业生产结果显示，只考虑单一特征点无法表征整个边降区状况，容易造成边部局部高点，内部边降无改善，如图1所示，图中 ΔED为各点边降偏差值，K为功效系数矩阵，ΔS为各机架工作辊窜辊增量.为了揭示上游机架工作辊窜辊对下游机架出口的调控功效，需要建立高效的带钢－辊系－机架间变形耦合模型，实现多机架连续计算，从而为工业生产提供理论支撑.

2 冷连轧过程金属变形分析

金属既在轧制区存在三维横向流动[7]，在机架间也存在显著的三维流动[4].辊缝中横向流动会造成边部区域延伸率小于中部，加剧了机架间塑性流动，并造成机架间张力变化，两者相互耦合.

2.1 轧制区内金属流动模型

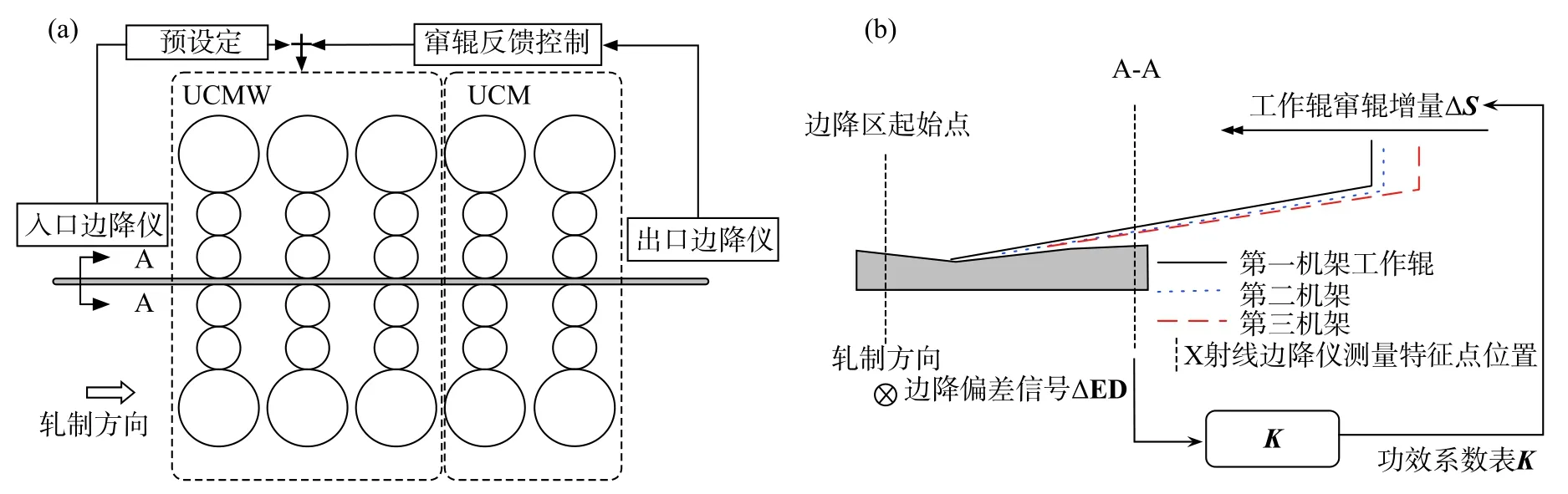
图1 边降自动控制系统（a）和工作辊窜辊调控功效系数（b）Fig.1 Schematic of edge drop control system (a) and schematic showing the effectiveness of tapered work roll shifting (b)

Pawelski等认为薄带钢在轧制区内各条元之间互不影响，直接使用卡尔曼微分方程求解宽度方向各条元位置轧制力，论证了其在低碳钢小凸度和负凸度轧制时的适用性.若将边降区横向流动视为纯剪切，引入轧辊弹性变形−轧件弹塑性变形有限元模型计算所得的横向流动因子[9]，则既可以避免三维全解析差分模型收敛性问题[10]，也能构建辊缝内三维金属流动的解析模型.因此可以借助如下假设条件简化模型：轧制区内沿宽度方向分条元，各条元之间互相不影响，中部为平面应变状态，边部考虑三维变形；边部各条元的横向流动由带钢表面剪切应力沿轧制方向的增量平衡.根据上述假设条件绘制薄带轧制受力分析图，如图2所示，图中hz为带钢在轧制区内的总厚度，x,y和z分别代表轧制、宽度以及厚度方向，σx为指向x方向在垂直于x轴的平面上的应力，τyx为指向y轴垂直于x轴平面的剪切应力，p为轧制压应力，适用小角度轧制假定，qx,qy分别为指向x，y的摩擦应力，σb为平均后张力，hentry与hexit分别为带钢各条元的入口与出口厚度，σf为初始设定平均张应力，作为前张力计算条件，B为带钢宽度，POST表示轧后屈服.针对带钢在轧制区内的弹塑性变形问题，列出近似求解空间问题的三大类力学方程.

2.1.1 力平衡方程

对图2所示的每个微元体，分别列出轧制方向和宽度方向力的平衡方程：

x，y方向的摩擦应力qx,qy的计算方法为：

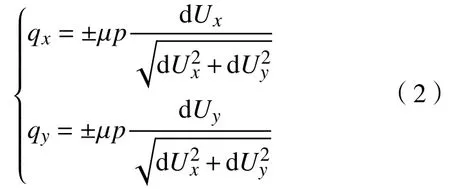
式中，μ为摩擦系数，dUx和dUy分别为薄带相对轧辊的轧制方向和宽度方向滑动位移阶段增量.

2.1.2 几何方程

位移增量dUx和dUy同应变增量的关系定义为：

式中，G为横向流动因子[9]，ε为真应变，xn为中性点位置.

2.1.3 物理方程

建立弹性区、塑性变形区应力−应变关系，在弹性区，扩展Le与Sutcliffe的处理方式至三维[11]：

式中，E为弹性模量，v为泊松比.首先对方程组（4）第一式对x求偏导，利用轧制方向力的平衡方程（1）可以消去未知量 dσx/dx.随后通过方程组（4）第二式消去未知量 dσy/dx，由于 σx+p单位为MPa远小于带钢弹性模量210 GPa，因此可以忽略.最终得到单位轧制力p的一次微分方程组：

公式（5）为带钢处于弹性变形区时，轧制单位压力p计算方法.当超过屈服条件后有：

图2 薄带轧制受力与变形分析图.（a） 正视图；（b） 侧视图；（c） 俯视图Fig.2 Force and deformation diagram of strip rolling: (a) front view; (b) side view; (c) top view

式中，YS为屈服强度.

2.1.4 横向流动因子

基于大量显式弹塑性有限元仿真的基础上，杜晓钟认为横向流动存在于边部区域，其区域的宽度是带钢厚度、压下量和摩擦系数的函数，横向流动的最大值是屈服强度和摩擦系数的函数[12−13].刘立文等[14]研究发现轧制时张力也会影响金属的横向流动.假设轧制区内横向流动因子的分布规律为[12]：

式中，y0为对应横向流动作用范围，Gmax为最大横向流动因数：

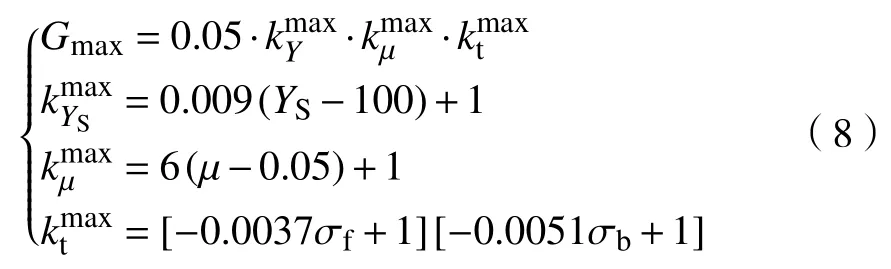
式中，r为压下量，kh，kr，kμ和kt分别为带钢名义厚度、压下量、摩擦系数和后张力同横向流动区域宽度之间的拟合函数.

2.2 轧后屈服模型

锥形工作辊窜动破坏了带钢等比例凸度关系，带钢延伸率之差超过限值时，带钢受大张力屈服，称为轧后屈服模型[4]，带钢变形情况如图3所示.考虑辊缝内横向流动，各条元在出口的伸长量为[13]：

式中，l'为出口条元长度，l0为入口条元长度，εy为各条元在轧制区内沿宽度方向应变，其值由式（3）得到.机架间带钢延伸率之差为：

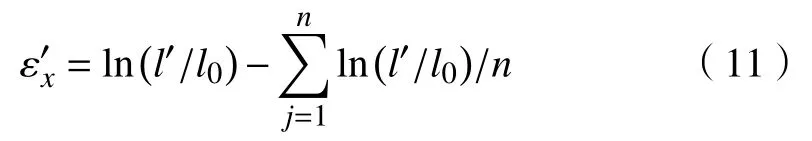
图3 整体计算流程Fig.3 Flow chart of the improved model

式中，n为沿宽度方向条元数量，j为各条元编号，式(11)等号右边第一项为各条元x方向应变，第二项为应变平均值.当应变率差造成的应力值超过屈服强度时，出现附加张力变形：

需要不断对出口应变率差以及应变平均值进行迭代，直至应变平均值不再变化.在Lee等研究的基础上，本文认为在带钢内部区域无宽展变化，横向流动区内为自由流动情况，从而得到塑性应变增量[4]：

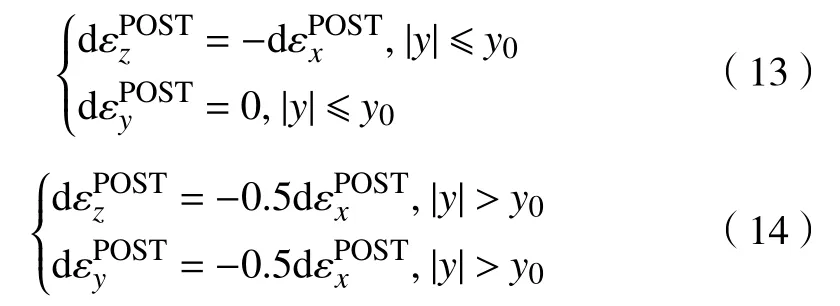
可以得到每个条元在机架间带钢断面厚度hPOST与宽度bPOST为：

式中，b为带钢各条元原宽度，由式(14)计算得到.则条元出现横截面面积减小情况：

式中，A为发生轧后屈服前的断面面积，ΔA为其增量，当机架间张力不变时，每个条元张应力值为：

2.3 整体计算流程

首先利用2.1中带钢三维解析模型计算带钢的轧制力分布，之后利用影响函数法[15]计算该轧制力分布时的辊系弹性变形，得到出口断面与延伸率差，进入2.2中轧后屈服模块，得到轧后屈服断面，当厚差残差值小于3 μm时结束迭代.单机架计算完成后，将断面、累计变形量、前张力和缩宽量作为已知条件，输入下一机架，整体计算流程如图3所示.若轧制方向网格密度为0.09 mm，宽度方向网格密度为10 mm，对于单机架计算时间大约为4 h（单CPU@4.0 GHz）.

3 模型验证

将本文所述模型计算结果同已发表的工业实验结果进行论证[11]，结果对比如图4（a）和（b）所示.可看到由于考虑了轧后屈服现象，对于边降区15～115 mm断面计算误差始终小于3 μm，误差最大处为距带钢边部0～15 mm，原因可能为最边部区域处于极端摩擦与变形状态，横向流动因子实际值与理论值的偏差大.根据图4（a）结果对比，由于机架间和轧制区内横向流动的存在，会降低锥形辊对本道次的边降调控效果.由图4（b），由于轧后屈服，上一机架工作辊窜辊造成的边部增厚会遗传至下一机架.

图4 模型验证.（a）第一机架计算结果;（b）第二机架计算结果Fig.4 Validation of model:(a)results of 1st stand;(b)results of 2nd stand

4 窜辊调控功效系数工业应用

边降调控功效为上游机架不同窜辊值对下游机架边降控制效率.定义边降区域为距带钢边部120 mm范围，选取三个边降测量特征点（距边部20、45与75 mm）.首先分别计算相同辊形在第1、2及3机架不同窜辊值(0、40、60、80和100 mm)时带钢断面同板差；随后，连续计算至下一机架出口边降值，轧制参数在表1中列出，从而求得三个边降特征点处调控功效系数，如下式：

表1 轧制参数表Table 1 Table of rolling parameters

由图5（a）可知，对于最靠近内部的第1特征点，第一机架窜辊效率最高，下游机架功效近乎为0.由图5（b）可知，对于中部的第2特征点，第二机架效率最高，第三机架功效近乎为0.由图5（c）可知，当窜辊量较小时，第二机架对边部特征点3的调控功效最高，当窜辊量增大边紧加剧后，第一、二机架功效减小，第三机架升至最高.这种下游机架边降调控宽度递减的规律，是由于连轧机机架间张力递增，厚度递减，下游机架的横向流动区宽度递减，因此边降调控的范围也在递减.归纳得到前三个机架工作辊窜辊调控边降的特征为：第一机架控制带钢内部的边降偏差，第二机架控制中部，第三机架控制边部.

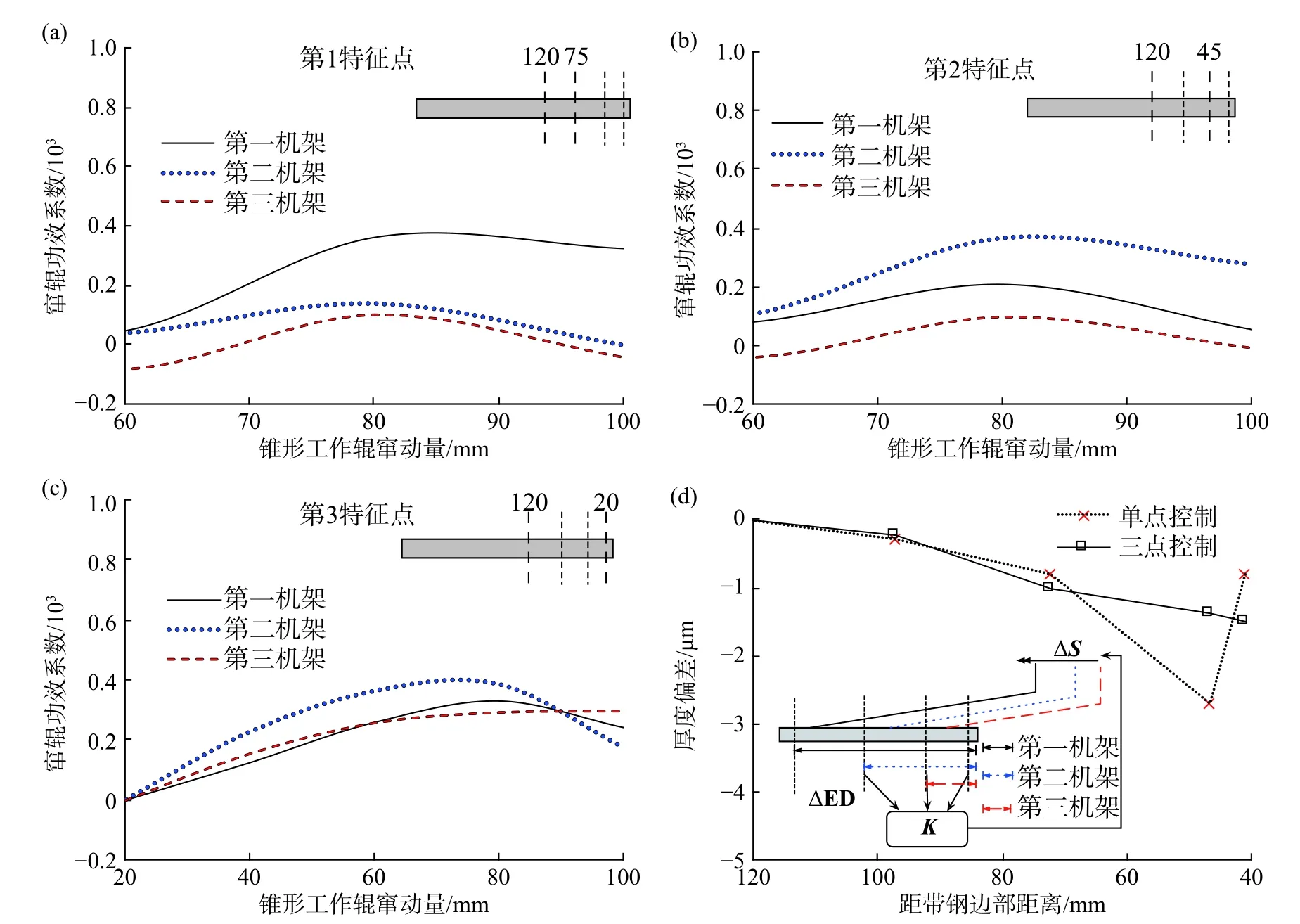
图5 锥形工作辊窜辊边降调控功效系数.（a）第1特征点；（b）第2特征点；（c）第3特征点；（d）三点配合调控策略应用效果Fig.5 Effectiveness of edge drop control of tapered work roll shifting: (a) at measuring Point 1; (b) at measuring Point 2; (c) at measuring Point 3;(d) applied effects of three-point control strategy

根据以上规律，设计了根据三个特征点的边降配合控制策略.该配合调控策略与使用效果如图5（d）所示，保证下游机架窜辊位不超过上游机架控制特征点位置.调控功效系数矩阵为下三角式，控制系统简便易行.当使用单点控制策略时，虽然边降区边部效果明显，但是内部偏差未消除.使用三点式配合控制时，内部偏差为0则第一机架无需窜动，中部偏差较大则需查功效系数表加大第二机架窜辊，外部偏差为0则需相应减小第三机架窜辊，从而消除整个边降区的偏差.该三点边降配合调控策略已被集成于国内首套完全自主知识产权的1500冷连轧边降自动控制系统中，已经长期稳定运行.

5 结论

（1）建立了高效的轧件-辊系-机架间的三维耦合数值模型，综合考虑了轧制区内金属横向流动与轧件轧后屈服行为，完成了两个机架连续仿真计算，经实验验证，在带钢边降区具有3 μm的精度.

（2）第一机架对距边部75～100 mm的边降偏差控制效率最高，距边部45～70 mm的边降偏差控制功效最高为第二机架，第三机架工作辊限定在控制距边部45 mm控制边部的偏差.

（3）针对不同机架所表现出来的边降调控有效宽度与功效系数，提出了根据三点边降偏差值的三机架配合调控策略.在工业生产中得到了实际应用，取得了良好效果.