饱和土有效应力原理下的水土压力分算和合算的统一计算
王国义 蒋宗全
(中电建成都建设投资有限公司,四川 成都 610212)
1 概述
目前地下空间的开发越来越快,工程设计中水土压力的计算力求既简便又精确,既不会造成安全隐患又不至于浪费。但水土压力计算问题长期困扰岩土工程界,曾经引起很大争论。尤其是水土计算公式中的“水土分算”与太沙基有效应力原理相符,“水土合算”与太沙基有效应力原理不相符问题争议最大。许多专家、学者致力于研究太沙基有效应力原理与“水土分算”“水土合算”的统一,并提出自己的观点。
魏汝龙[1]教授提出由于弱渗透性粘土中,土压力对支护结构的影响在短时间内难以得到体现,以至于有人认为有效应力原理不适用于这类粘土,并论证了用总应力强度指标进行“水土分算”的合理性;杨晓军、龚晓楠[2]认为“水土合算”只是一种经验方法,没有实际的理论依据;王洪新[3]把土的孔隙比、界限含水量、颗粒分析等物理参量引入水土压力计算中,提出一个水压力比率,把有效应力强度指标和总应力强度指标统一在一个强度公式中。并且给出了一个“水土分算”和“水土合算”的算法,实现了两者结果之间的过渡;刘发前[4]提出对于单粒结构而言,“土压力”为土颗粒与所吸附结合水对地下结构物的作用;对于近似于絮状的结构,大部分流体水受到土颗粒的吸引、絮状结构的束缚无法形成流动水,有效土压力降低,水压力大打折扣,这就是粘性土中实测水土压力接近于“水土合算”的原因。方玉树[5-8]提出水压率的概念,在此基础上修正了孔隙水压力、浮力、浮重度等的计算方法。李广信[9-12]根据方玉树提出的水压率概念进行了反驳,并提出了自己的观点,坚持有效应力原理的正确性,但对于“水土合算”与太沙基有效应力不相符问题指出还需进行研究与探讨。方玉树和李广信学术上讨论多次,但很明显都在坚持自己的观点,不能形成统一意见。两位专家对学术认知的执着值得大家学习。
目前大部分专家都认为粘性土中采用“水土合算”,砂性土中采用“水土分算”,与现场实测值较为接近。“水土分算”符合有效应力原理,但是仅在砂性土时与现场实测接近;粘性土采用“水土合算”相当于对水压力进行了折减,不符合有效应力原理。实际上,“水土分算”与“水土合算”许多问题没有解决,急需找到一正确水土压力计算公式,实现“水土分算”与“水土合算”的统一,并符合太沙基有效应力原理,从理论上提供水土压力计算依据。
笔者一直从事盾构施工技术与管理,在研究盾构压力平衡时对水土压力计算稍有涉猎,并进行了认真学习。在研究太沙基有效应力原理、水土压力计算和拜读各位专家论文时偶有灵感:“会不会向笔者[13]刚刚发表的《盾构平衡压力理论计算与应用技术》论文一样,以前有效应力原理研究的基础有误差或者是我们对有效应力原理的实际本质认识不足,导致后序研究偏离正确轨道”。
笔者对饱和土的理想断面进行分析,根据饱和土的几项已知参数和应力平衡原理推导出饱和土的总应力、土骨架应力和水应力三者之间的关系公式(饱和土应力公式)。将推导出的饱和土应力公式应用于典型饱和土的水土压力计算,计算值与现场实际基本相符,达到了“水土分算”与“水土合算”的统一计算。饱和土应力公式中给水度的引入,实现了所有类型饱和土的水土压力计算的统一。由于笔者推导出的饱和土应力公式与太沙基的有效应力原理公式不同,土骨架应力中有一部分是孔隙水压力的作用结果,优化了太沙基有效应力原理中有效应力和中和应力的计算值。因此正确与否需待各位专家、学者进行判断,也请各位专家、学者批评指正。
2 有效应力原理释义
太沙基从试验中观察到在饱和土体中土的变形及强度与土体中的有效应力密切相关,并建立了有效应力原理:σ=σ′+μ。其中,σ为平面上法向总应力,kPa;σ′为平面上有效法向应力,kPa;μ为孔隙水压力,kPa。有效应力原理表示研究平面上的总应力、有效应力和孔隙水压力三者之间的关系:当总应力保持不变时,孔隙水压力与有效应力可以相互转化,即孔隙水压力减小等于有效应力的等量增加。
根据有效应力原理,作用在饱和土体中的总应力由土中的两种介质承担:一种是孔隙水中的孔隙水压力,另一种是土颗粒形成的骨架上的有效应力。而土的抗剪强度是由有效应力决定的[14]。
以前的有效应力原理都是按以上所述解释的。大部分专家、学者也是按此原理进行深入研究。研究过程中有的专家、学者发现研究结果与实际不相符,提出了质疑,并试图对太沙基的有效应力原理进行修正,但至今还无让大家完全认可的计算公式。
3 饱和土应力公式的推导与水土压力计算
3.1 饱和土应力公式的推导
在研究有效应力原理时,方玉树[6]指出:孔隙水压力涉及的截面应同土体内力涉及的截面一样是颗粒之间通过的宏观上是平面的曲面;李广信[11]指出:饱和碎散的颗粒状材料情况下,取作用面时不要切断土颗粒,而是通过颗粒间的接触点。现有专家在研究有效应力原理时,所取应力截面一般为土颗粒接触点间的相连曲面。李广信[9]在论文中也研究了所取的截面穿过颗粒,通过推导计算认为无论如何切割结果是一样的,关键在于接触面积可以忽略及“有效应力是颗粒间同方向的力被总面积除”。
无论力还是应力平衡都是在一个平面上的研究,因此现对饱和土体进行ab水平面与ac竖直面切割,截面穿过土骨架中的土颗粒,研究其饱和土的应力关系(如图1所示)。
现对饱和土应力进行理论推导,假设研究的水压力都是静水压力,由于渗流产生的动水压力这里不进行研究。设土体为饱和均质土体(水面与土体等高),高度为h,饱和土体容重为γsat,ab水平面面积为A,饱和土体静止侧压力系数为k0,水容重为γw,ab水平面上的孔隙水压力为μ。
由于水颗粒非常小,假设水颗粒未被切割,但土骨架中的土颗粒被切割。ab水平面上孔隙水占一部分面积,被切割的土颗粒的切割面面积和在ab水平面上土颗粒接触点的面积之和占一部分面积。为了准确区分这两部分面积,引入土的给水度。给水度定义:饱和的土壤或岩层在重力作用下排出的水量与土壤或岩层体积的比值。由于给水度符号与孔隙水压力符号(μ)相同,现假设给水度符号为m。假设饱和土为均质土体,给水度定义中排出的水在饱合土中也是均质的,那么在每一个饱和土的截面中水所占的面积都与m有关。
设饱和土体截面中水面积与截面面积比值为m1,饱和土体截面单边水占的距离与整个单边距离比值为x,从而可求出m1。将饱和土体截面上的土颗粒和水分开示意(如图2所示)。

由于m=x3,从而计算出:m1=x2=m2/3。
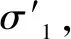
根据应力平衡原理为:
(1)
μ=γwh
(2)
μ1=γwhm1
(3)
σ1=γsath
根据式(1)可推导出ab水平面上土骨架的竖直应力:
(4)
3.2 水土压力计算公式的推导
现对基坑支护中的水土压力进行计算。根据现有土力学理论,土骨架的竖直应力会产生静止侧向土压力,水应力向各个方向等值传递。
设P总=P土+P水,其中,P总为静止侧向水土压力总压力;P土为静止侧向土压力;P水为静止侧向水压力。

(5)
P水=γwhm1
P总=P土+P水=k0(γsat-γwm1)h+
γwhm1=(k0(γsat-γwm1)+γwm1)h
(6)
为下文叙述方便,现将笔者推导出的饱和土应力公式和水土压力计算公式分别定义为饱和土应力公式和水土压力计算新公式,太沙基有效应力原理和原水土压力计算公式分别定义为太沙基有效应力原理和水土压力计算原公式。
3.3 水土压力计算实例验证
根据水土压力计算新公式和原公式,结合饱和土参数对水土压力进行验证。
设土体为饱和均质土体(砂卵石或粘土地层,水面与土体等高),高度h=10 m,饱和土体容重γsat=23 kN/m3,饱和土体静止侧压力系数k0=0.4,水容重γw=10 kN/m3。砂卵石地层给水度m=0.25,粘土地层给水度m=0.027。求ab水平面上a点的侧向水土压力。
当m=0.25时,m1=0.4;当m=0.027时,m1=0.09。
1)按水土压力计算新公式计算水土压力。
砂卵石地层基坑侧向水土压力为:
P总砂=(k0(γsat-γwm1)+γwm1)h=
(0.4×(23-10×0.4)+10×0.4)×10=116 kPa。
粘土地层基坑侧向水土压力为:
P总粘=(k0(γsat-γwm1)+γwm1)h=
(0.4×(23-10×0.09)+10×0.09)×10=97.4 kPa。
2)按水土压力计算原公式计算水土压力。
砂卵石地层基坑侧向水土压力(水土分算)为:
P1总砂=(k0(γsat-γw)+γw)h=
(0.4×(23-10)+10)×10=152 kPa。
粘土地层基坑侧向水土压力(水土合算)为:
P1总粘=k0γsath=0.4×23×10=92 kPa。
3)水土压力计算新公式与原公式的计算结果对比分析。
根据水土压力计算新公式可以看出,除给水度m不同,其他饱和土参数相等前提下,计算出来的水土压力值不同,给水度m值越大,水土压力值越大。这主要是由于给水度m值越大,孔隙水压力的作用力对截面产生的水应力越大导致的。这与现场实际相符。
由水土压力计算新公式与原公式的计算结果可以看出,新公式计算出来的水土总压力值小于原公式水土分算值,大于原公式水土合算值,与实际情况更相符。水土压力计算新公式实现了“水土分算”与“水土合算”的统一计算,比水土压力计算原公式更接近于实际。
4 太沙基有效应力原理与饱和土应力公式的区别
根据太沙基有效应力原理公式和推导出的饱和土应力公式式(1)、式(3)、式(4)可以看出,两个公式有本质上区别,完全不同。为研究清楚,现对土骨架在ab水平面上被切割的一个土颗粒进行分析(如图3所示)。
设被切割的土颗粒在ab水平面上形成de水平面,面积为A1,通过其他土颗粒和此被切割土颗粒传递给de水平面的竖直向下力为p1(重力和浮力的合力),孔隙水对此土颗粒切割面产生压力(de水平面向上无孔隙水压力),设孔隙水压力对此土颗粒切割面产生的竖直向下力为p3,de水平面的反作用力为p2。
p3=A1μ。
根据力的平衡原理:
p2=p1+p3=p1+A1μ
(7)
如果将土骨架在ab平面上所有被切割土颗粒和接触点在ab平面上的土颗粒竖直向下合力设为p,由式(1)、式(7)可知:
(8)
从式(5)、式(7)、式(8)可以看出,饱和土体中土骨架对ab水平面的竖直向下力是土骨架重力、土骨架所受水浮力和此水平面孔隙水压力对土骨架切割面产生的竖直向下力的合力。土骨架应力是上述三个力的合力在截面上的平均应力。孔隙水压力的一部分转化为土骨架应力,由于饱和土给水度m的不同,孔隙水压力转化为土骨架的应力相应发生变化。
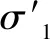
5 饱和土有效应力原理的实际应用解释
饱和土有效应力原理的建立,可以合理解释现今土力学的争议。但有的人会问:实际施工挡土墙时,土颗粒直径很小,不可能被切割,这与实际情况不符,应该如何解释。
当在施工挡土墙(如连续墙)时,土颗粒不可能被切割,挡土墙与原状土断面不可能为绝对平面,浇筑混凝土时会自动填充原状土的不平面(如图4所示)。如果挡土墙附近原状土没有任何变形,土的参数没有变化,土中土骨架应力和水应力没有发生改变,就可以使用饱和土应力公式进行水土压力计算。

当然,如果施工过程中挡土墙附近的原状土产生变形,产生变形土的给水度相应发生变化,变形土会有一个新的平衡,需要使用新平衡土的参数计算水土压力。
6 饱和土有效应力原理定义与解释
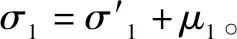
饱和土有效应力原理实际上就是应力平衡原理。土是单个土颗粒或多个土颗粒形成的固体与水的混合体,当固体较多时各种特性与固体相类似,当水较多时各种特性与流体相类似,土根据水、土颗粒的含量占比而表现出不同的固体或流体特性。太沙基在对中和应力和有效应力解释时存在问题:饱和细粒土上方加一定高度的水压应力,饱和土无可觉察的压缩;饱和土上方加同等应力的铅丸,饱和土有明显变形。因此断定孔隙水压力是中和应力,总应力与中和应力的差值就是有效应力。这种判断是有误的。太沙基试验中饱和土上方增加水压应力由于孔隙水的存在,水压是对单个土颗粒产生内力挤压,单个土颗粒很难产生变形,理论上就算单个土颗粒变形,周围的水也会及时填充变形空隙,因此饱和土不会有明显变形。铅丸是直接作用在饱和土上,饱和土的抗剪强度很小,因此会发生明显变形。流体(水)和固体(铅丸)的压力对饱和土的作用对象不同,导致产生的结果不同。
太沙基有效应力原理只适用于一种情况:饱和土中每个土颗粒都以单粒存在,每个土颗粒与土颗粒之间都有孔隙水,此时孔隙水压力为中和应力,对饱和土变形无影响。当饱和土中两个或多个土颗粒粘结成一不规则体(现实存在的土基本都是这种情况),由于孔隙水压力的存在,孔隙水压力产生的力作用到不规则体上,当不规则体土颗粒间的粘结力无法承受孔隙水压力作用产生的有效应力时,不规则体会挤压变形,此时孔隙水压力已经不是中和应力。太沙基有效应力原理出现问题的本质是太沙基不应该将孔隙水压力作为中和应力,推出的有效应力就是不准确的。
7 结论
1)通过引入土力学中的给水度并加以运用,纠正了太沙基有效应力原理的不足,形成了饱和土有效应力原理。2)作用在基坑侧面上的水应力不是孔隙水压力,而是孔隙水压力产生的作用力在截面上的平均水应力,可以认为是中和应力。3)饱和土中孔隙水压力产生的作用力一部分作用到土骨架上,孔隙水压力对土骨架的静止侧向土压力有一定影响。土骨架应力可以认为是有效应力。4)水土压力计算新公式实现了“水土分算”和“水土合算”的统一计算(即水土分算),理论正确,能够准确计算水土压力,并更加接近实际值。“水土分算”是在饱和土有效应力原理下的“水土分算”。5)饱和土有效应力原理是优化了太沙基有效应力原理,可以作为理论土力学其他公式推导的基础。凡是由太沙基有效应力原理推导出来的公式应采用饱和土有效应力原理重新推导。
8 结语
笔者偶有灵感后向多位专家咨询过土力学的基础,张波教授级高级工程师指出我认为的有效孔隙率应该是大家承认的给水度,杨其新教授告之笔者现阶段专家对太沙基有效应力原理存在质疑,但还无法将此理论优化,并取得认可。笔者经过近半个月的冥思苦想,终于完成此篇论文。前人对太沙基有效应力原理提出过质疑,因此才会有水压率、水压力比率等多个假设,但由于未突破孔隙水压力和孔隙水压力传递给截面的平均水应力这道坎,观点始终未取得大家认可。笔者不想推翻什么,只是希望通过自己的努力,如果在太沙基有效应力原理的基础上,优化的饱和土有效应力原理正确,能对中国乃至全球理论土力学的发展有所帮助,这才是笔者想尽快将此论文发表的初衷。

