基于神经网络的叶丝填充率影响因子量化研究
裴莉莉,余 婷,李 伟,户媛姣,石 丽
(长安大学,陕西 西安 710000)
0 引言
制丝环节是卷烟加工过程中重要的一步[1-3],由于其工艺流程复杂,涉及参数众多,使得叶丝填充率常常处于波动中[4]。不稳定的叶丝填充率将严重影响后期烟丝填充值,而烟丝填充值是卷烟质量评价中的重要指标之一[5],因此该问题会导致品牌卷烟质量稳定性下降。成品叶丝填充率在一定程度上能够决定卷烟的耗丝量,其值的大小和波动直接影响到烟支的质量及其稳定性[6-7]。近些年来,国内对烟丝填充值和叶丝填充率都积极地开展了研究[8]。2014年,唐军等[9]对烟丝填充值和烟支质量及其稳定性做了相关性分析,结果表明两者呈线性相关。2017年,崔升[10]首次探讨了HXD工艺参数对烟丝质量的影响。2018年,张明文等[11]利用离子色谱仪开展了叶丝干燥工序对烟丝成分含量影响的研究;同年,邱承宇等[12]设计正交试验分析了制丝温度对叶丝质量的影响。2019年,张雯等[13]利用相似性原理对烟丝结构分布稳定性评价;同年,方利梅等[14]提出了一种结合K均值聚类算法和改进遗传算法的自动烟丝掺配工艺。虽然国内对叶丝的重视程度也在逐渐上升,但从研究量来说还是很少的,并且结合当下高效而准确的人工智能手段的文献也极为有限。为了进一步提升烟支质量并保持其稳定性,利用人工智能中常用的数据分析模型,深入挖掘制丝工艺中各个流程参数对叶丝填充率的影响是极为必要的[15]。
本文主要对卷烟厂生产数据进行多源异构数据融合与数据清洗,之后采用相关性分析和机器学习中MLP神经网络,分析制丝过程中的生产参数对叶丝填充率的影响,为叶丝生产过程提供了科学、有效的参数优化及重点参数稳定性监控的指导。
1 数据集构建
1.1 原始数据
浙江某卷烟厂提供其制丝阶段工艺流程和制丝全过程各工序数据参数,以及不同批次工单的生产数据,共四类数据表,分别为生产过程统计数据表、叶片过程检验数据表、叶丝过程检验数据表以及批次工单对应关系数据表,具体原始数据表的基本信息如表1所示。
1.2 叶丝填充率数据集构建
卷烟厂制丝阶段的工艺流程图如图1所示,本试验探究的是“自动开包→叶丝装箱”的全过程。由图1可以看出,流程分A、B、C 3个生产流水线,虽然数据分为3块,但实际只有2个工段,其中松散一次加料和二次加料为制叶段,烘丝为制丝段。再通过1.1和1.2介绍的方法,构建数据表,得到28个生产过程参数,1776组批次数据用于分析,其中包括A线294组、B线754组、C线728组。

表1 原始生产数据

图1 制丝阶段工艺流程图
2 数据质量的提升与相关性分析
2.1 多源异构制丝数据的融合及数据的清洗
由表1可以看出,每种表的结构以及特征是不同的,因此需要利用多源异构数据融合技术对表进行整合,同时为了探究制丝工艺中各个参数的变化对叶丝填充率稳定性的影响。本试验对全线数据进行差分处理,从而得到最终可用于相关性分析的数据表。由于四类生产及检验数据表中都存在着缺失数据和异常数据,因此需要运用数据清洗手段将这些异常值找到并采用“人机协作”的方式对错误数据进行检测与消除。
2.2 相关性分析与特征选择
相关性分析是数据挖掘的一种重要方法,结合该方法可以给出特征因子之间的相关性,也可以得到特征因子与待测指标之间的相关性,并进行特征选择。由于制丝阶段工艺复杂、需要分析的参数较多,利用目前较为流行的数学统计模型较为合理,同时本试验所采用的数据量上万条,也确实能够满足统计分析的要求。因此分别采用Pearson、Spearman相关性指数对叶丝填充率的影响因子进行分析,最终对相关性进行量化,Pearson、Spearman相关性指数的计算公式分别为:
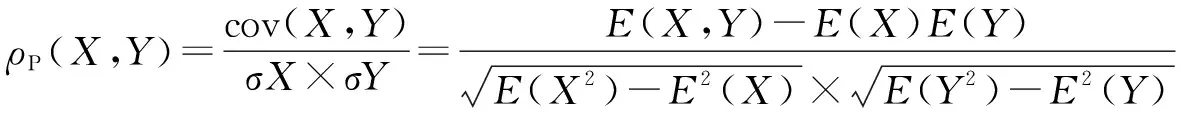
(1)
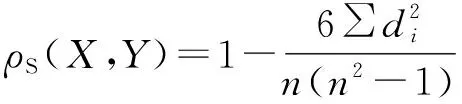
(2)
式中X、Y分别为特征因子数据集,cov(X,Y)为X,Y的协方差,E表示数据集的数学期望;n为X、Y两变量的等级对字数,即样本含量;di为同对等级之差(i=1,2,3,…,n)。
对A、B、C线和整体分别进行相关性分析,由图2可以看出,2种相关性分析方法分析出的结果较为一致,不存在需要单独讨论的参数值。
为了更好地完成参数重要性权值的量化,本试验选取2个指数的平均值作为整体不分线时的重要性权值,具体的权值量化表如表2所示。同时将影响因子进行排序,由图3可以看出,制丝过程参数对叶丝填充值稳定性影响的变化。KLD排潮风门开度、SIROX蒸汽薄膜阀开度、KLD总蒸汽压力、KLD热风风门开度、冷却温度、1区蒸汽薄膜阀开度、KLD热风蒸汽薄膜阀开度、冷却水分、2区蒸汽薄膜阀开度、SIROX后温度对叶丝填充值稳定性的影响较大,因此在生产过程中应严格控制该指标,从而保证叶丝生产的稳定性。
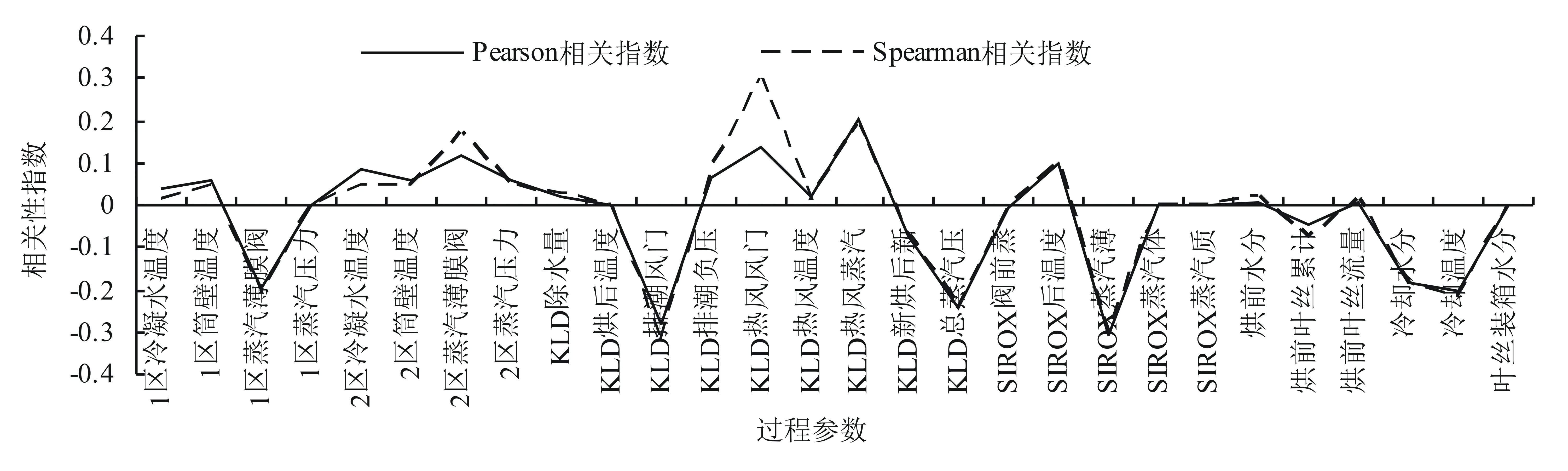
图2 制丝过程参数对叶丝填充率的相关性分析

表2 制丝过程参数量化权值
3 MLP神经网络模型对叶丝填充率影响因子的量化
3.1 MLP神经网络原理的概述
利用MLP神经网络对叶丝填充率进行量化与验证,利用真实值与预测值的平均绝对误差及线性相关系数对结果进行评价,所用神经网络结构如图4所示。

图3 制丝过程参数对叶丝填充率的影响
MLP神经网络最突出的特点是通过误差的反向传播来反复修正权值和阈值,使得误差函数值达到最小,准确度达到预期标准。式(3)表示了MLP神经网络的误差函数:
(3)
式(3)中,dj表示输出节点预测值,yj表示真实值;n为测量值的总个数。
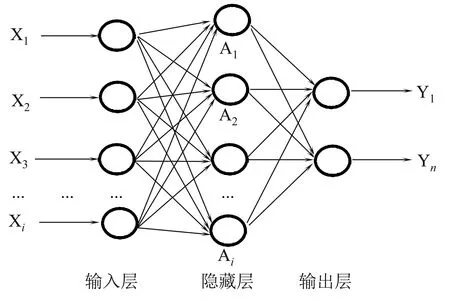
图4 MLP神经网络模型
在反向传播的过程中,最常用的误差最小化方法为梯度下降算法,即沿着相对误差平方和的最快下降方向,对网络超参数进行调整。在网络训练过程中,通过学习率的设定使得每次反向传播迭代后总体的误差逐渐减小,最终达到系统可以接受的范围,即获得最优权值。以上过程具体实现可由图5表示。
为了更加准确地得到制丝过程中不同的流程对叶丝填充率的影响,需要在计算模型训练完成后对有影响的主导因素再次利用模型训练的方式进行分析。本项目采用敏感性分析的方法,通过影响的权重大小来衡量不同过程参数对叶丝填充率的影响程度。实现框图如图6所示。
具体实现方法为:
(1)使用影响特征变量进行模型训练,得到最优模型M1,记录准确率为P1;

图5 MLP算法模型优化流程
(2)对M1权重系数进行分析,舍弃权重系数最小的3%的值(非主导因素)对应的因素变量;
(3)对第2步中非主导因素去除后的因素重新进行模型训练,得到最优模型M2,记录其准确率为P2;
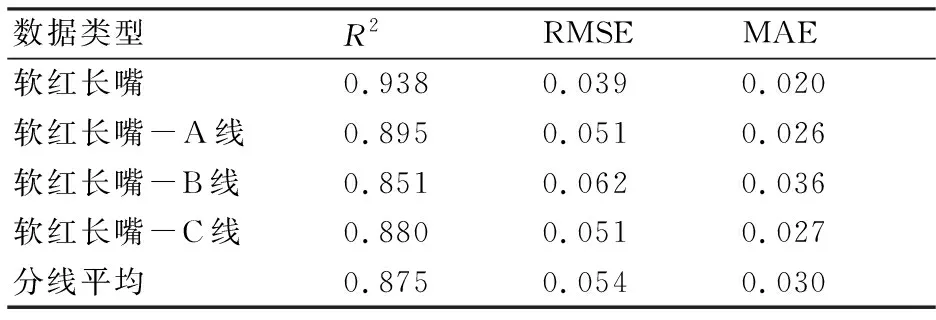
(4)判断若P1>P2,则M1传入第7步;若P1 (5)对M2重复第二步分析,并继续第三步,得到M3和P3顺序执行第4步,判断P2与P3的关系; (6)迭代以上步骤,得到精度最高的模型Mi; (7)认为此模型中的权重系数均为显著影响因素。可认为这些因素为主导因素,并分析各自因素影响的大小。 用MLP神经网络模型对填充率进行量化,并对相关性分析结果进行验证,分线及整体准确率如表3所示。由表3可以看出,整体不分线将数据放入模型时的验证精度明显高于分线时的精度,可见数据量越大,结果越准确。 表3 MLP神经网络模型性能结果 真实值及验证值的对比如图7所示,从图7中可以看出,输入28个变量时,软红长嘴整体分析的R2为0.938,均方根误差为0.039,平均绝对误差为0.020。预测结果误差相对较小,具有较高精度。软红长嘴分为A、B、C三个生产流水线分析时,A线的R2为0.895,均方根误差为0.051,平均绝对误差为0.026;B线的R2为0.851,均方根误差为0.062,平均绝对误差为0.036;C线的R2为0.880,均方根误差为0.051,平均绝对误差为0.027。同时由图8也可以看出真实值与验证值的变化趋势一致,说明实验结果合理准确。 图8 MLP神经网络模型的预测结果对比 本文基于制丝工艺流程及多源异构的烟厂生产线数据,首先利用数据融合及数据清洗技术构建制丝工艺过程参数数据集,之后利用2种不同的相关性分析方法对浙江某卷烟厂软红长嘴的制丝流程中各个参数及叶丝填充率进行了相关性分析,得到制丝过程参数的相关性指数及其量化后的重要性权值。最后,利用机器学习中MLP神经网络模型对叶丝填充率的参数因子的权重进行量化并对结果进行验证。结果表明,叶丝填充率的真实值与验证值平均绝对误差仅为0.020,说明本研究得到的相关性排序及其量化结果是很有意义的,通过改善以上重点影响因子的波动能够很好地指导制丝过程,提高叶丝填充率的稳定性,从而提升品牌烟支质量。3.2 基于MLP神经网络的填充率影响因子量化与验证结果

4 结论

