重力坝深层抗滑稳定失稳判别标准探讨

王小毛

摘要：深层抗滑稳定是重力坝设计中的重要问题。传统的刚体极限平衡法虽然计算简单且有丰富的工程实践，但无法分析坝基的破坏发展过程。数值分析可以模拟坝基应力、变形和破坏机理，在深层抗滑稳定分析中逐步得到广泛应用。基于有限单元法和有限差分法，通过强度折减分析重力坝深层抗滑稳定，探讨了不同失稳判别准则下稳定安全系数的差异性。以葛洲坝水利枢纽为例，采用有限单元法和FLAC3D显式差分法进行了重力坝深层抗滑稳定分析。结果表明，采用塑性区贯通判别准则进行抗滑稳定分析可行有效，控制标准可取为塑性区达到建基面宽度的15%。研究成果可为重力坝深层抗滑稳定设计提供参考。

关键词：重力坝，深层抗滑稳定，失稳判别标准，有限单元法，FLAC3D显示差分法，葛洲坝水利枢纽

中图法分类号：TV642.3文献标志码：A DOI：10.15974/j.cnki.slsdkb.2020.02.001

1研究背景

重力坝是我国高坝建设中的主要坝型之一。当重力坝坝基内存在缓倾角软弱结构面时，坝体可能沿软弱结构面产生滑移，影响大坝安全。因此，开展重力坝深层抗滑稳定研究对保障大坝安全具有重要意义。

由于重力坝深层抗滑稳定问题的复杂性，其分析方法尚无统一规定。刚体极限平衡法将滑移的各块岩体视为刚体，以抗滑力和滑动力之比作为安全系数来判断滑移体的稳定性，其具有丰富的工程经验和成熟的设计准则，应用最为广泛，是SL319-2018《混凝土重力坝设计规范》主要推荐的方法。但该方法不能确定滑移体的位移和滑移面上的应力分布，因此不能探索稳定破坏机理及发展过程。限于刚体极限平衡法的局限性，复杂地质条件下重力坝深层抗滑稳定的应力应变分析已成为该领域科研及工程技术人员关注的重点。

随着计算机软硬件水平的提高，数值分析法可以结合应力、变形和破坏机制综合分析，模拟各种复杂的边界条件，使深层抗滑稳定分析更为科学合理，在工程中应用日益广泛。常用的数值分析方法包括有限单元法、有限差分法等连续介质方法以及离散元法、非连续变形分析等不连续介质方法。有限单元法、有限差分法的理论与工程应用均较为成熟，可以模拟复杂的坝基地质条件以及坝体和坝基材料的非线性本构关系，分析区域应力、变形的空间分布和塑性区发展过程，但该方法在应用中对安全的定义、失稳状态的判据等问题尚未形成统一的标准。

基于此，本文结合工程案例，采用有限单元法及有限差分法探讨了重力坝深层抗滑稳定分析的失稳状态判别标准，可为重力坝深层抗滑稳定设计提供参考。

2抗滑稳定安全系数计算与失稳判别准则

采用有限单元法和有限差分法，离散研究对象，建立平衡方程，可获得研究区域的位移场和应力场，在此基础上可进行安全系数计算和稳定状态判别。

2.1 安全系数计算方法

2.1.1 应力代数和比值法

应力代数和比值法是借助数值分析的应力成果计算出滑面上的正应力和剪应力，再求出滑面上的抗滑力和滑动力，各个滑面上的抗滑力代数和与滑动力代数和的比值即为抗滑稳定安全系数。对于滑裂通道分为N段的直线型滑面，安全系数计算见下式：

2.1.2 超载法

超载法假定岩体抗剪强度参数不变，通过不断增加作用在大坝上的荷载（水压力）研究坝体渐进破坏过程，当设计荷载增加Kp倍后，坝基深层抗滑稳定达到临界状态，則称Kp为抗滑稳定超载安全系数。常见的超载法包括超水容重法和超水位法。

2.1.3 强度折减法

强度折减法是O.C.Zienkiewicz等在1975年首次提出的，该方法主要考虑坝基岩体强度参数的不确定性和可能的弱化效应，通过强度折减系数k降低岩体的凝聚力C和内摩擦系数f，并将折减后的强度参数C和f代人数值模型中再次试算，判断岩体各个单元弹塑性状态以及位移变化，当岩体发生失效破坏时，对应的强度折减系数k即为该工程的安全系数。

C=c/k （2）

f=f/k （3）

式中，k为强度折减系数;C，f，C，f分别为折减前后的凝聚力、内摩擦系数。

应力代数和比值法与刚体极限平衡法安全系数定义相近，具有明确的力学概念，但要求已知坝基潜在滑裂面，且未考虑滑面单元的应力方向，在实际应用中具有一定局限性。超载法需要成倍增大工程荷载，而实际大坝出现的超载系数较小，渐进破坏过程与实际情况并不相符，同时，坝体上游水压力超载，将导致坝踵部位应力集中程度加剧，改变了坝基潜在的失稳模式，因此仅能作为衡量大坝安全程度的相对指标，不能反映大坝的实际安全度。强度折减法可以模拟坝基从局部破坏到整体破坏的渐进失稳全过程，能够反映大坝一坝基系统可能的失稳模式与滑移通道，符合失稳破坏机理。一般情况下，强度折减法与超载法计算结果差异较大，而与应力代数和比值法、刚体极限平衡法计算结果相同或相近，且该方法在实际工程应用最为广泛，故本文采用强度折减法求解抗滑稳定安全系数。

2.2 失稳状态判别方法及准则

采用强度折减法得到的安全系数和坝基失稳状态判别密切相关，常用的判别准则包括收敛性准则、特征点位移突变准则、塑性区贯通准则等。

（1）收敛性准则。该准则认为当坝基处于极限平衡状态时，非线性有限元方程组的迭代计算过程或显性有限差分法不平衡力计算结果将不收敛。当主要由塑性区扩展范围太大导致的迭代计算不收敛时，可作为系统失稳的依据。

（2）特征点位移突变准则。该准则认为系统进入极限状态时，失稳部位会产生塑性流动，滑移面上特征点位移与强度折减系数关系曲线也会发生突变，出现明显拐点。因此，可将位移曲线变化拐点对应的强度折减系数作为安全系数。

（3）塑性区贯通准则。运用强度折减法计算过程中，随着坝基材料强度不断降低，坝基内产生塑性变形不断扩大，当塑性区相互贯通以至于形成滑移通道时，即可认为系统达到临界失稳状态。塑性区判别方法包括大变形发生和变形速率增加等。

坝基临界失稳状态判别具体采用哪一种判别准则，目前尚无统一标准。收敛准则中收敛条件和迭代次数均会影响模型收敛性，因此，计算不收敛并不一定代表坝基已达到极限状态。特征点位移突变准则中特征点和位移曲线拐点的选取是否具有代表性特别重要，但具有一定的主观性。塑性区贯通准则直观形象、客观合理，在工程中应用较为广泛，但需注意塑性区判别及贯通比例对安全系数的影响。

3 工程案例

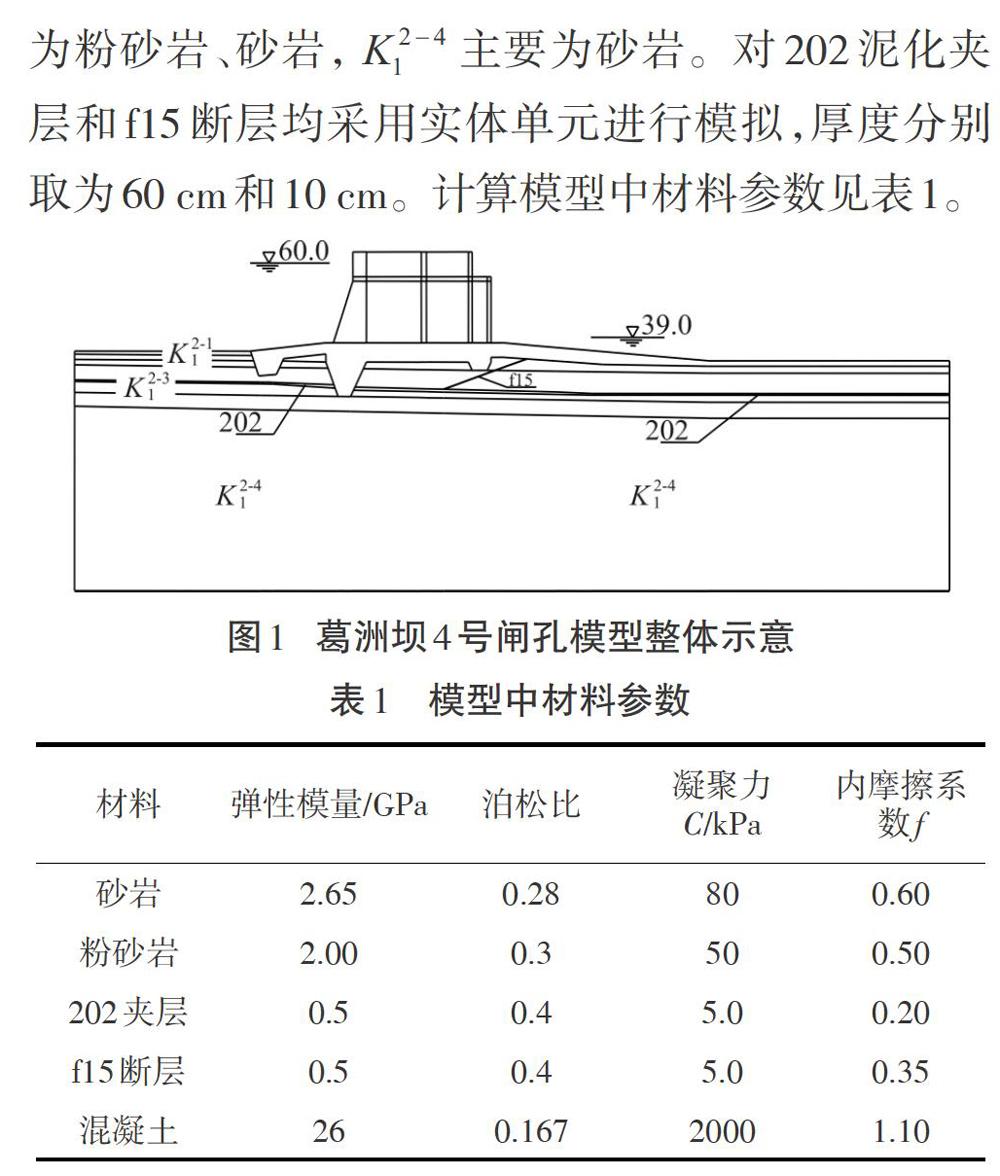
本文以葛洲坝水利枢纽为例，采用有限单元法和FLAC3D显式差分法进行重力坝深层抗滑稳定分析，对两种数值分析方法的计算结果和不同失稳判据对应的安全系数差异性进行探讨。

3.1计算模型

选取对闸体抗滑稳定较为不利的闸门关闭状态作为计算工况，上游水头为66m，下游水头为39m。计算域的底边和侧向采用位移法向约束，岩体屈服准则采用Druker-Prager內接圆模型，安全系数计算采取强度折减法，临界失稳状态判别准则采用特征点位移突变准则、塑性区贯通准则和收敛性准则。

3.2 特征点位移突变准则

特征点位置分布见图2，有限差分法模拟结果见图3。当强度折减系数为3.00-3.50时，特征点位移发生突变，在关系曲线上形成了明显的拐点，安全系数取为3.30。

采用有限单元法，当折减系数小于3.70时，特征点位移变化比较缓慢，之后呈现大幅度增加趋势（见图4），因此安全系数取3.70。从极限状态的位移云图（见图5）和位移矢量图（见图6）可以看出，闸基在202泥化夹层和f15断层处均发生了较大的剪切滑移。

3.3 塑性区贯通准则

取塑性区贯通时的强度折减系数作为整体安全系数。由有限差分法模拟结果可知，当强度折减系数为3.50时，闸室前端部分单元出现拉剪破坏，闸室末端和f15断层与202泥化夹层之间部分出现小范围的塑性区;此后塑性区快速发展，当强度折减系数为3.54时，上下游塑性区贯通（见图7）。

采用有限单元法，首先在f15断层与202泥化夹层连接部位出现小范围的塑性区，此后随着强度折减系数的不断增加，塑性区不断发展，当强度折减系数为3.80时，上下游塑性区贯通见图8。

3.4收敛性准则

采用收敛性准则，有限差分法得到的安全系数为3.58，有限单元法得到的安全系数为4.10。

3.5 安全系数差异性探讨

不同失稳判别准则对应的安全系数见表2。从表中可知，两种数值分析方法的计算结果规律一致，有限单元法计算结果稍大。不同失稳判别准则得到的安全系数存在一定差异，收敛性准则对应的安全系数最大，位移突变准则对应的安全系数最小。

对于收敛性准则评判坝基失稳破坏过程，从特征点位移来看，当计算不收敛时位移已经很大或者位移增加速度已开始加快，说明此时系统已进入不稳定状态，因此采用收敛性准则得到的安全系数结果是上限值。对于特征点位移突变准则，当特征点的位移曲线出现拐点时对应的强度折减系数作为安全系数，与实际的坝体破坏特征相符合，但拐点的精确位置不易确定。对于塑性区贯通准则，由特征点的位移变化可知，当坝基的塑性区贯通后，位移增加速度与之前相比明显加快，位移突变和滑移路径塑性区贯通基本同步，所以采用塑性区贯通准则是合适的，有条件时可采用两种判据综合确定坝基安全系数。

在坝基的渐进破坏过程中，塑性区扩展曲线有一个明显的稳定阶段，该阶段之前大坝基本处于弹性状态，此阶段末的塑性贯通率一般小于14.67%。随后，坝基随强度折减系数的增加，塑性区呈快速扩展的不稳定状态。本文采用传统刚体极限平衡法得到的安全系数对应的塑性区贯通率约为15%，可以将塑性区范围达到建基面宽度的15%作为临界控制标准。

4 结论

本文以葛洲坝水利枢纽为例，采用有限单元法和有限差分法，通过强度折减探讨了重力坝深层抗滑稳定性，分析了不同失稳判别准则下安全系数的差异性。结果表明：基于数值分析法进行重力坝深层抗滑稳定分析时，采用强度折减法计算安全系数较合适，以塑性区贯通作为判别准则有效可行，控制标准可取为塑性区达到建基面宽度的15%，其与SL319-2018《混凝土重力坝设计规范》中深层抗滑稳定分析具体内容是一致的。