基于Matlab GUI的麦克斯韦速率分布可视化研究

郝振莉 吕良军

摘  要： 以研究麦克斯韦速率分布智能可视化为主线，以Matlab GUI为交互平台，直观形象地展示分布函数，并从多个角度动态地分析气体分子运动速率分布的特点。基于不同的条件及研究角度动态地做出动态的图像，实现课堂教学的高度交互性，有助于学生深刻理解麦克斯韦速率分布，提高课堂教学的效果。

关键词： Matlab GUI; 麦克斯韦速率分布律; 分布函数

中图分类号：O551          文献标识码：A     文章编号：1006-8228（2020）04-07-04

Study on visualization of Maxwell's velocity distribution using Matlab GUI

Hao Zhenli1，2， Lv Liangjun1，2

（1. Mathematical modeling teaching and applied research center， Kaifeng， Henan 475004， China; 2. Yellow River Conservancy Technical Institute）

Abstract： Taking the intelligent visualization of Maxwell's velocity distribution as the main line and using Matlab GUI as the interactive platform， the distribution function is displayed intuitively and vividly， and the characteristics of the velocity distribution of gas molecules are analyzed dynamically from multiple perspectives. Making images dynamically based on different conditions and research angles can help students deeply understand Maxwell's velocity distribution and improve the effect of classroom teaching.

Key words： Matlab GUI; Maxwell's velocity distribution law; distribution function

0 引言

麥克斯韦速率分布律是分子动理论的重要结论之一，它是研究气体分子碰撞、大量分子热运动服从统计规律性等问题的重要理论依据，正确理解它对学习热力学非常有用。但是由于推导困难、公式复杂、曲线难画，麦克斯韦速率分布律学习起来比较费力，成了热学理论教学中的一个难点。

Matlab软件是目前国际上最流行、应用最广泛的科学工程软件之一，其集成了数值计算、矩阵计算和图形绘制等功能，广泛应用于研究及解决各种数学及工程计算问题，它提供了使用方便、功能强大的计算分析平台。Matlab GUI平台实现了人机交互，不但使计算更加简捷明了，同时还可执行动作和变化来满足用户的需求，从而可以设计别具风格的交互界面。

文献[1]中指出，在物理教学中利用Matlab，可以建立动态直观的物理图像，有助于学生更好地理解物理概念，提高学习兴趣，调动学习积极性。本文利用Matlab GUI对麦克斯韦速率分布律的智能可视化处理为主线，研究系统的可视化操作界面的结构设计、功能设计、以及控件的选择和布局、控件功能的实现。

1 麦克斯韦速率分布曲线

麦克斯韦速率分布律指出[2]，在平衡态下，理想气体分子速率分布在区间v～v+dv内的分子数占总体分子数的百分比为：

⑴

其中，T为气体的热力学温度，μ为气体分子的质量，k为玻尔兹曼常量，，由此可得麦克斯韦速率分布函数为：

⑵

以f（v）为纵坐标、v为横坐标画出的f（v）-v曲线，称为麦克斯韦速率分布曲线，如图1所示。因这些是概率分布，所以每条曲线下的面积为1，即

⑶

它形象地描绘出气体分子按速率的分布情况，由式⑴可知，图1中任一区间v～v+dv内曲线下的阴影小竖条的面积为：。

在有限速率区间v1～v2内曲线下的阴影面积为：，其物理意义是，速率分布在v1～v2的分子数占总分子数的百分比，或一个分子的速率在v1～v2内的概率。

速率分布曲线表明，速率很小和很大的分子数占总分子数的百分率都较小，而具有中等速率的分子数占总分子数的百分率较高，当v=vp时f（v）取极大值，vp称为最概然速率，也称最可几速率，其物理意义是，如果把整个速率范围分成许多相等的小区间，则分布在vp所在小区间的分子数占总分子数的百分比最大。

2 温度、气体分子质量与麦克斯韦速率分布曲线的关系

由f（v）的表达式⑵可知，速率分布曲线的形状与气体温度T和分子质量μ有关。同一气体，当温度升高时，分子热运动加剧，即速率较大的分子数及其占总分子的百分率增大。另外，分布曲线还需满足归一化条件 即曲线下的总面积等于1，所以温度升高时，分布曲线向右移动，f（v）的极大值减小，曲线变得较为平坦。

在温度一定的情况下，不同气体分子的质量不等，麦克斯韦速率分布曲线会随分子质量的改变而有所改变。由函数的极值条件可知，满足

将麦克斯韦速率分布函数式⑵代入上式，即最概然速率

⑷

由式⑷可知，当分子的质量增加，其最概然速率减小，即在相同温度下，质量较大的分子运动的剧烈程度较小，分子质量越小，其运动就越剧烈最概然速率也越大，分布在高速率区间的分子数百分比就越大，分布也越趋均匀。

3 麦克斯韦速率分布的GUI设计

图形用户界面（GUI）是由窗口、光标、按键、菜单、文字说明等对象构成的一个用户界面。用戶通过一定的方法如鼠标或键盘选择、激活这些图形对象，使计算机产生某种动作或变化，比如实现计算、绘图等[3]。MATLAB GUI开发环境提供了一套可视化的创建图形窗口的工具，方便用户在此环境下开发界面并可快捷地创建GUI应用程序， 它可以根据用户设计的GUI布局，自动生成M文件的框架，用户可在这一框架编制自己的应用程序。

3.1 构思草图布置控件

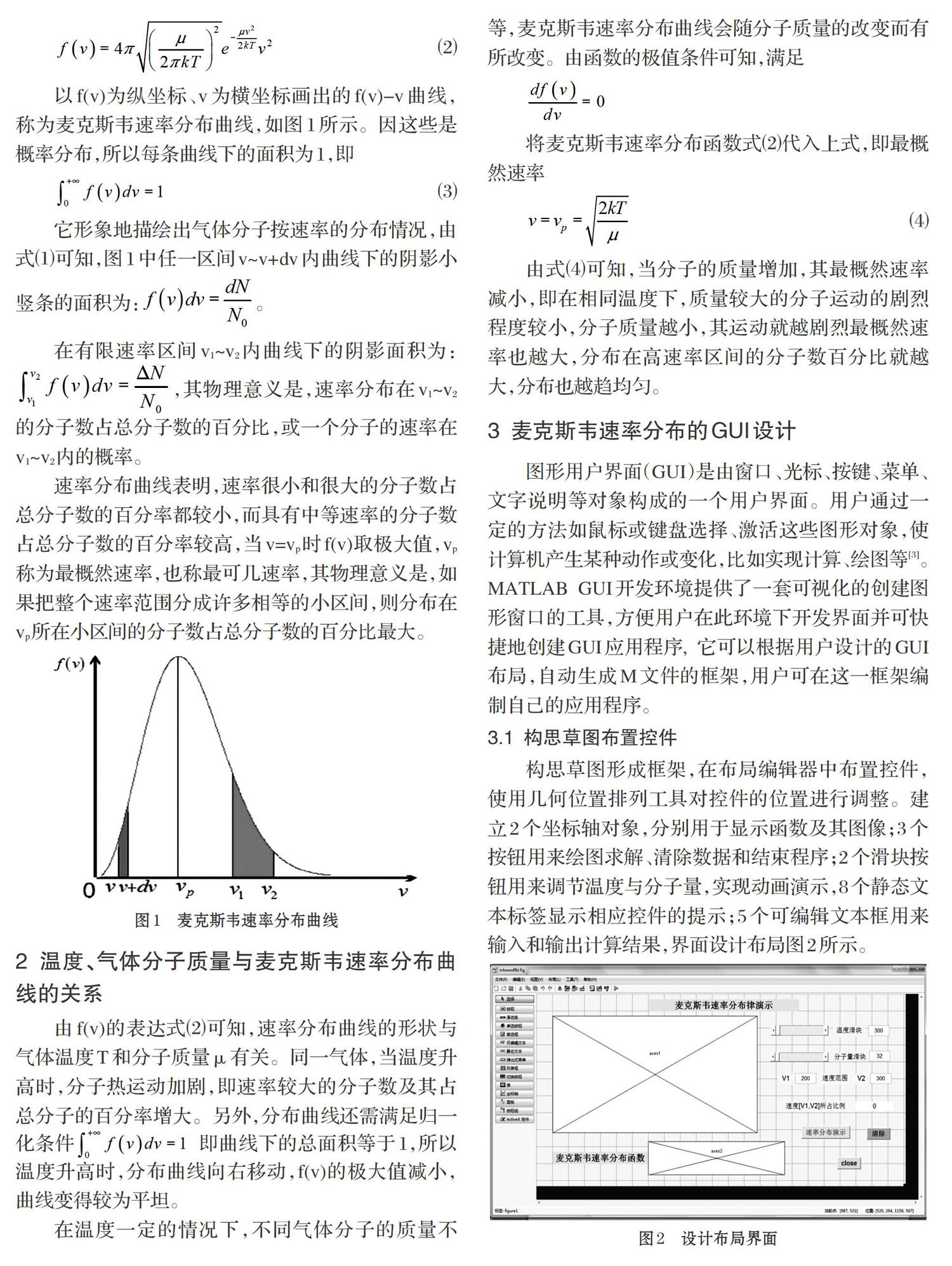
构思草图形成框架，在布局编辑器中布置控件，使用几何位置排列工具对控件的位置进行调整。建立2个坐标轴对象，分别用于显示函数及其图像;3个按钮用来绘图求解、清除数据和结束程序;2个滑块按钮用来调节温度与分子量，实现动画演示，8个静态文本标签显示相应控件的提示;5个可编辑文本框用来输入和输出计算结果，界面设计布局图2所示。

3.2 设置控件的相关属性

控件的标识Tag是对各控件的识别，每个控件创建时都会由开发环境自动产生一个标识，在程序设计中，为了编辑、记忆的维护的方便，一般为控件设置相对应的标识，便于程序的调试。

3.3 编写代码，实现控件的功能

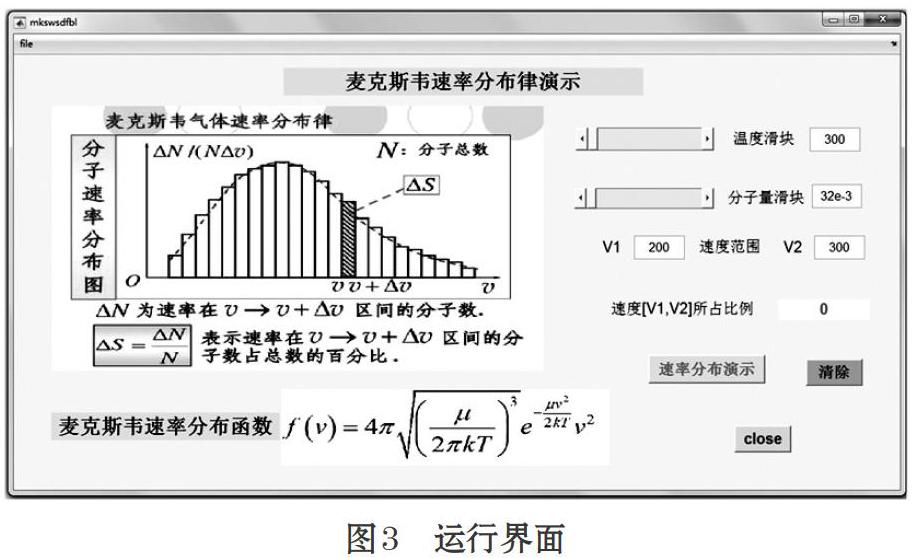
编写代码，完成程序中变量的赋值、输入、输出及绘图等工作，打开editor在相应的按钮命令后面添加相应的代码[4]，实现各按钮的动作功能。运行后得到如图2的gui运行界面。

4 麦克斯韦速率分布智能可视化演示

单击“温度滑块” 按钮两侧的三角形箭头时[5]，温度可在200～800K之间变化，麦克斯韦速率分布曲线就会出现向右移动并趋向平缓的动画效果，说明同一气体当温度升高时，分子热运动加剧，即速率较大的分子数及其占总分子的百分率增大。

移动“温度滑块”按钮中间的滑块，分别获取T=200K，367K，800K时，就出现如图4所示的分布曲线，非常形象地观察出同一气体在三种不同温度下的速率分布变化规律，温度越高则vp增大，但f（vp）值变小，分布曲线变平坦，高度降低。

同样的，在温度不变的条件下，单击“分子量滑块” 按钮两侧的三角形箭头时，分子质量可以在0.002～0.102kg之间变化时，分布曲线就会出现向左移动并趋向陡峭的动画效果。移动“分子量滑块” 按钮中间的滑块，分别获取T=0.002kg，0.0162kg，0.0363kg时，就出现如图5所示的分布曲线，非常形象地观察出三种气体在同一温度下的速率分布变化规律，分子质量μ越大vp越小，但否f（vp）值变大，分布曲线变陡峭。

编辑温度，分子量，速度范围，单击速度分布演示按钮，运行结果如图6所示。具体数据见表1。

从图6和表1中可以得出结论：当温度增加，分子质量减小，分布曲线变平坦，分子运动在相同的区间间隔下概率变小。

上述GUI界面设计理论是用户可以根据示图的效果来调整精度[6]，在每次使用中，只需在相应的编辑文本框中输入实测数值，单击相应按钮就可实现对应求解，简单快捷明了，真正实现了人机交互功能，十分方便工程人员多次重复使用。

5 结束语

借助于系统提供的操作功能，通过自行设置参数和设计GUI界面，实现了数据的可视化，不仅加深对麦克斯韦速率分布的直观认识，同时还可以对程序进行二次开发和应用，在教学中可鼓励学生自行设计与开发，体验创新的乐趣，充分激发学生的学习兴趣，提高教学效果。

参考文献（References）：

[1] 蔡莉莉，张琳.Matlab在麦克斯韦速率分布律中的应用[J].大学物理实验，2013.8：75-78

[2] 王少杰，顾牡.吴天刚主编.新编基础物理学[M].科学出版社，2017.

[3] 吕良军，郝振莉.Matlab GUI在水力计算中的应用[J].黄河水利职业技术学院学报，2015.7：47-50

[4] 陈垚光，毛涛涛，王正林等.精通MATLAB GUI设计[M].电子工业出版社，2011.

[5] 汤剑锋，欧阳锡成.基于Matlab GUI麦克斯韦速率分布律的数字化教学研究[J].中国教育技术装备，2013.12：129-130

[6] 吕良军，梁童，张兵等.梯形明渠特征水深计算的GUI实现[J].河南科学，2016.5：726-731

[7] 徐斌，陈浩.基于Matlab软件GUI功能对气体分子麦克斯韦速率分布的比较分析[J].物理与工程，2015.3：84-88

[8] 史强，高学喜等.关于麦克斯韦速率分布律的教学探讨[J].聊城大学学报：自然科学版，2014.4：30-31

[9] 高娟，汤永新等麦克斯韦速率分布函数的简单推导和讨论预览[J].长春大学学报，2014.8：1057-1058，1066

[10] 汤剑锋，欧阳锡城.基于Matlab GUI的麦克斯韦速率分布律的数字化教学研究[J].中国教育技术装备，2013.36：129-130

[11] 安宇.麦克斯韦速率分布率的实例[J].大学物理，2013.7：20-21

[12] 任继阳，王黎黎等.麦克斯韦速率分布律的模拟演示[J].玉溪师范学院学报，2012.4：33-34

[13] 王明美.几何画板在麦克斯韦速率分布律教学中的应用[J].广西物理，2012.4：53-55

[14] 王向贤，朱浩瑞.基于MATLAB的麦克斯韦速率分布函数的数字化教学[J].宜春学院学报，2011.4：17-19，63