不可运算与不可计算*
许 煜
今天我选择这个主题,是因为在我看来“不可计算”[incalculable]这一概念是贝尔纳·斯蒂格勒[Bernard Stiegler]思想的核心,也是他关于运算理论的新基础的研究项目的核心。
一
在《递归与偶然》一书中,1Yuk Hui,Recursivity and Contingency,Rowman and Littlefiled International,2019;中译本见许煜著、苏子滢译,《递归与偶然》,华东师范大学出版社,2020年。我尝试通过递归性和偶然性这两个概念,对莱布尼茨[Gottfried Wilhelm Leibniz]以来的西方哲学史做出解读。我们知道,递归函数是计算机科学的学生和从业者都十分熟悉的。对于包括曾经的我在内的大多数计算机科学一年级学生来说,递归是个困难而又令人兴奋的课题。同时,熟悉控制论的人也一定知道,递归或递归性在所谓的二阶控制论中,被用作反馈[feedback]一词的代名词。因此,递归这个术语直接包含着许多含义,也正是这种模糊性,允许我们开创一个新的概念领域,以反思计算机科学和哲学之间的关系,并把递归概念扩展至计算机科学和欧洲现代哲学之外。但更重要的是,我希望通过区分不可计算性和不可运算性,把递归概念作为阐释不可计算性的基础。
在《递归与偶然》中,我指出递归的概念可以追溯至康德在1790年出版的《判断力批判》中所说的“反思”。康德开启了一种新的认识论,不同于他在1781年的《纯粹理性批判》中发展的那种认识论。这种认识方式在《道德形而上学基础》(1785)以及稍后的《实践理性批判》(1788)关于定言命令[kategorischer Imperativ]的部分中已经讨论过,但只有到了第三批判中才得到充分的阐释,正因如此,康德在序言中表示,第三批判是第一批判和第二批判之间的桥梁。这一关键是康德在《判断力批判》中所阐述的反思性判断,这是审美判断和目的论判断的基础。反思性判断与规定性判断不同。
在康德看来,规定性判断是一种把普遍者应用到特殊者之上的判断—比如当先验范畴被看做感官材料必须服从的框架的时候。范畴是普遍的,对一个对象的经验则是特殊的。反思性判断不是将普遍套用于特殊,相反,它从特殊者开始,通过启发式地推导出自己的规律而走向普遍。规定性判断和反思性判断的差别很大,从认识论的角度看,人们可以说规定性判断对应着一种机械论的世界观,按照这种态度,所有的存在都是机械的存在。就像在笛卡尔那里,可以把人体理解为教堂里的管风琴;管道是容器,风是动物的灵魂。反思性判断则与有机体类似,因为它不是预先规定好的,它的存在类似于一种生命形式。
规定性判断和反思性判断的差异,是假言命令[hypothetischer Imperativ]和定言命令,构成性[konstitutiv]和调节性[regulativ],或者更进一步来说,机械体和有机体之间的差异。这一差异对于包括费希特[Johann Gottlieb Fichte]、谢林[Friedrich W.J.Schelling]和黑格尔在内的后康德观念论者来说是根本的,他们都分别讨论过反思性判断并发展出自己的递归模型。笛卡尔的机械体是有限的,它无法解释机械性的目的以外的存在,因此前“批判”时期的康德已经激烈反应:动物身体如何可能!?动物身体不像钟表,钟表的每个部分都与邻近的部分相连接,但独立于整体;而动物的身体只能被理解为一个全体,其中每个部分都相互关联,也都和全体关联。用我们现代的语言来说,机械暗含着一种线性逻辑:A-B-C;而有机意味着一种非线性逻辑,即A-B-C-A’。
在《递归与偶然》中,我试图通过把递归性从运算和控制论领域延伸到不限于机器操作的广义逻辑,来拓展递归性的概念;因为在人与机器、技术与环境、有机与无机之间的关系中,也能发现递归性。康德的《判断力批判》深受他那个时代有机概念的影响,如今它已经发展为一种有机主义[organicism];概括地说来,我们可以总结出三种由此产生的思路。第一种是胚胎学的研究者和历史学者提倡的有机主义;第二种是控制论,或者是我所说的机械有机主义[mechano-organism],它始于1948年左右,以机器学习和人工智能的形式延续至今;第三种是器官学[organology],它始于1907年法国出版的柏格森[Henri Bergson]的《创造进化论》,后来在乔治·康吉莱姆[Georges Canguilhem]于1947年发表的〈机器与有机体〉[Machine et Organisme]一文中被明确表达,再由吉尔伯特·西蒙栋[Gilbert Simondon]和贝尔纳·斯蒂格勒等人进一步阐释。2见许煜,《递归与偶然》,第三、四章。在这里,我将只关注机械有机主义,并在结尾处提到器官学;在某种程度上,我希望表明这种路径如何有助于信息学理论的重建。
二
诺伯特·维纳[Norbert Wiener]在1948年出版了《控制论》,书的第一章的标题为“牛顿主义与伯格森主义的时间”[Newtonian versus Bergsonian Time]。在这一章中,维纳提出这样一个论点,即机械论和生机论之间的经典区分已不再有效。机械论是线性的,重复的;柏格森的时间概念所阐释的生机论则是非线性和创造性的;然而维纳表示,柏格森主义的时间,也就是说有机体的行为,可以被控制论机器吸收。控制论机器不同于时钟那样的传统机械论机器,因为它具有基于反馈和信息的操作,这种技术在詹姆斯·瓦特[James Watt]蒸汽机的“调速器”[governor]中已经有所应用。
正是在这种情况下,维纳声称,“现代自动化和活的有机体一样,存在于柏格森式的时间中,按照柏格森的思路,没有理由认为活有机体的基本运作模式不应该与这一类自动化相同[……]事实上,整个机械论-生机论的争论已经被降级为表述不恰当的问题”。之后,我们还可以在《生命现象学》[Phenomenology of Life]作者、哲学家汉斯·约纳斯[Hans Jonas]那里读到这样的确认:“对经典文献因疏忽而留下的二元论的克服:自亚里士多德以来,我们第一次有了一种统一的学说[……]对现实的再现[representation]。”
在所谓的一阶控制论中,“反馈”的说法是用来描述自我调节的机制。在二阶控制论中,“递归”一词更经常被扩展到机器操作以外的其他社会和政治领域。例如,尼克拉斯·卢曼[Niklas Luhmann]将温贝托·马图拉纳[Humberto Maturana]和弗朗西斯克·瓦雷拉[Francesco Varela]的自生[autopoiesis]概念应用于对社会运作的研究,发展出了被称为系统理论[systems theory]的社会学领域。递归是自动化的关键,这种形式的自动化基于可计算性的原则。在详细解释可运算的/不可运算的[incomputable]与不可计算的区别之前,让我们先来看看递归和可计算性的关系。
在计算机科学中,递归函数仅意味着“一个函数在执行过程中调用自己”。给一年级计算机科学学生的递归函数的一个简单例子,可以产生一个有限的斐波那契数列:0,1,1,2,3,5,8,13,21,34,...,数列中后面的数字是前面两个数字之和。这样,34 之后的下一个数字将是55(21+34)。如果要求我们列出数字n 之前的所有斐波那契数——n 可以是任何数字——简单的办法是创建一个计数到n 的迭代(循环)。尽管它被称为循环,我们还是可以把这种循环方式理解为线性的重复。递归的版则本没有这么直观。它指一个函数调用自己,比如f(n)=f(n-1)+a。我们设n=5,或许能更清楚地看到它每次是如何调用自己并展开的:
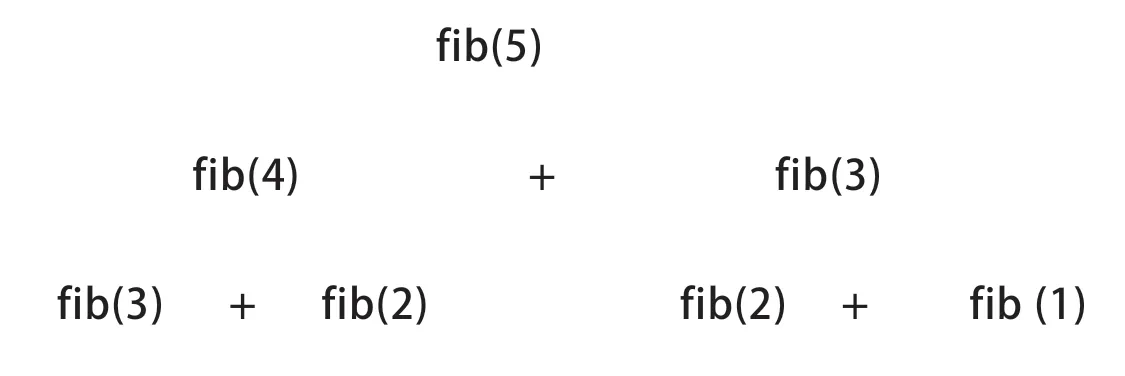
递归产生了超出迭代(只是重复)的复杂性,因为它由许多个螺旋式循环组成,而不是只是一个机械的重复循环。迭代听起来像是环状的,但它其实是一种线性逻辑,因为它线性地重复同一个过程。从运算的角度来看,递归可以让运算时间(也就是到达输出的时间)大大减少。且这不只是单纯的效率问题。递归可枚举的[recursively enumerable]也意味着可运算的,也就是说,人们可以找到一种能在有限的步骤中产生这个数字的算法。如果一个数字不是递归可枚举的,它就是不可运算或不可判定的。例如,库尔特·哥德尔[Kurt Gödel]否定地证明了戴维·希尔伯特[David Hilbert]在1928年所说的判定性问题[Entscheidungsproblem],即一种算法,它能在给定一组公理和一个数学命题的情况下,判断这个命题能否由公理证明。哥德尔的创见主要可以从两个方面来理解。首先,哥德尔用数字——如今这种方法称为哥德尔配数法[Gödel numbering]——把逻辑命题转换为数字,如下表所示:

符号配数符号配数0 1 x 9 10+3╞11 S 2 1 12=5∃13 X 4∧14)7→15(6∀.8
用数字取代限定词,使哥德尔能把符号命题转化为算术,这样人们就能专注于计算而不是不同命题的形式逻辑推演。其次,哥德尔还开发了一个递归函数以执行数学证明。3在哥德尔之前,托拉尔夫·斯科伦[Thoralf Skolem]已经提出用数字取代逻辑限定词,以递归地证明一个逻辑命题的有效性。引自Rod Adams,An Early History of Recursive Functions and Computability:From Gödel to Turing,Docent Press,2011,p.22; 另见Yuk Hui,On the Existence of Digital Objects,University of Minnesota Press,2016,chapter 6,“如果我们认为算数的基本定理是有功能的断言,并把思维递归模式看做基本,那么科学就可以严格地建立起来,用不着罗素和怀德海的‘总是’和‘有时’的概念”,这也可以表述为:可以为运算提供逻辑基础,无需使用明显的逻辑变量。哥德尔在1934年发展了现在人们说的一般递归函数。4在哥德尔之前,也已经有理查德·戴德金[Richard Dedekind]这样的先驱,他提出用递归函数把数学操作形式化。他的一般递归函数在数学上等价于通用图灵机和阿隆佐·邱奇[Alonzo Church]的λ 演算。
运算递归性[computational recursivity]提供了自生结构[genetic structure]的认识论证明,正如费希特、谢林、黑格尔这些浪漫主义者和观念论者试图构建的那样。(在法国,我们可以在皮埃尔·利维[Pierre Livet]和让-克里斯多夫·戈达德[Jean-Christophe Goddard]的早期作品中看到这种构建。5见Pierre Livet,"La notion de récursivité,de la première cybernétique auconnexionnisme",Intellectica,no.39,vol.2,2004,pp.125-137 以及Jean-Christophe Goddard,"Autonomie,re duction et re flexivite:la philosophie naturelle de Francisco J.Varela et le projet transcendental",Intellectica,no.36-37,2003,pp.205-225。)观念是自设定[Selbstsetzung]、自调节的[Selbstbedingung],因此它对观念论者和概念艺术家来说有巨大的潜力。在今天的递归算法中,这种对观念的“机械证明”会造成什么呢?一些观察者设想这样一个观念:宇宙是一个完美的递归生成的整体,其中每个生命都是同一发生过程的独特实例。我们可以称之为柏拉图式的证明,就像柏拉图在《蒂迈欧篇》[Timaeus]中谈到的造物主对世界的数学设计,其中实存的世界只不过是观念世界的实例。
这正是现代运算理论的基础,如果我们讨论一个运算的世界,就意味着在这个世界中,一切在有限步骤内都是可枚举的。即使递归是运算的基础,这并不是说所有用编程语言实现的思想都是递归的。比如我们可以写一个简单的程序,输出“Hello,World!”。

即使这个执行在硬件层面上是递归的,程序的逻辑也只是程序性的或机械性的。当我们根据不同数量级[orders of magnitude]而不只是抽象的普遍意义来分析递归性的概念时,我们必须记住这一点。递归不只是运算性的思维,它更是一种与机械论对立的认识论。我们在今天的机器智能中,也能发现格雷戈里·贝特森[Gregory Bateson]所说的这种“递归认识论”。我们知道,神经网络最初是由沃伦·麦卡洛克和沃尔特·皮茨[Warren S.McCulloch and Walter H.Pitts,1943]提出的,他们把神经元想象为布尔函数[Boolean functions],把网络想象为多层神经元,它们的运作允许逻辑推论。神经网络的进一步发展,使明斯基[Marvin Minsky,1967]做出了这样的声明:“具有布尔神经元的神经网络可以模拟任意的有限自动机”,以及之后海基·海蒂涅米[Heikki Hyötyniemi,1996]的声明:“神经网络可以模拟任意图灵机”。6Mark Burgin,Super Recursive Algorithm,Springer,2005,p.66.
到目前为止,我们可以看到递归是运算的发展的一种基本认识论。如果一个问题可被编程为递归函数,就说明它是可运算的。如果有可运算者,就也有不可运算者,也就是不可决定者[undecidable];但是不可运算者,或者说不完整性,并非是不可计算的,这恰恰是因为按照定义,不可计算性不能是一个数学概念。我们可以说存在是不可计算的,正因为它不是数学概念。我们或许还想补充说,这是以生命为研究对象的器官学和机械有机主义之间的根本区别。当我们说上帝是不可运算的,上帝就沦为一个数学概念,因为不可运算性仍然是一个数学概念,换句话说,它是通过与可运算性的对立获得意义的。
三
不可计算性在今天的运算中是如何具体体现的?
在此我们或许可以回溯人工智能的历史,看看不可计算的问题如何被误解为认知问题,以及——如果我们在这里愿意遵循斯蒂格勒关于重建运算理论的基础的建议——我们如今该如何重新解释它。
20世纪70年代,美国哲学家休伯特·德莱弗斯[Hubert Dreyfus]发表了一系列关于人工智能的限度的著作,尤其是他的《计算机不能做什么?人工理性批判》[What Computers Cannot Do? A Critique of Artificial Reason]。书中,他指责人工智能科学家,尤其是马文·明斯基,把认知局限于“特定的知识或模型结构”。事实上,明斯基并非没有注意到这一批判,这位人工智能的创始人在1961年的重要论文〈走向人工智能〉[Steps Towards Artificial Intelligence]中承认道:“当然,关于‘智能’并不存在一种被普遍接受的理论;这里的分析是我们自己的,它或许很有争议。”7Marvin Minsky,“Steps Toward Artificial Intelligence”,Proceedings of the IRE,Volume 49,Issue 1(Jan.1961),pp.8-30,8.这意味着大概没有对智能的“客观”或“普遍”定义,因此它向各种解读开放。
可以把德莱弗斯的批判理解为对海德格尔《存在与时间》第一部分,尤其是第17 和18 节的一种实用的解读。17 节、18 节的标题分别是“指示与符号”[Reference and signs]和“相互关联性与意义:世界的世界性”[Involvement and significance:the worldhood of the world],海德格尔在这里确立了分析工具和符号,即指示[reference,Verweisungen]的本体论基础,以及相互关联性[involvement,Bewandtnis]如何规定指示的结构,例如工具与人的此在的相遇。德莱弗斯继海德格尔之后表明,明斯基等人对认知的本体论假设从根本上说是笛卡尔式的。或者用海德格尔的话说,笛卡尔式的智能把它前面的对象简单地看作在手之物[Vorhandene],立于主体的对立面[Gegenstand],且必须被当做某些属性的持有者。这种在手预设了笛卡尔式的机械逻辑。
德莱弗斯主张考虑一种与海德格尔所说的“上手”[Zuhandene]相对应的具体化的认知,这意味着我面前的事物不仅作为某些属性的持有者出现。相反,它的存在方式会受到世界的制约——世界是一种时间结构,它把认知和遭遇的对象联系在一起。比如在使用锤子时,我们并不思索锤子的形状和颜色,因为一个呈现为关系之网或指示之全体的世界,已经内嵌于认知之中。8參见许煜著、李婉楠译,《论数码物的存在》,上海人民出版社,2019年,第三章。我们可以把德莱弗斯的说法解读为对按照线性机械思维——而非递归的有机思维——来理解认知的批判。他的结论是,人工智能的困境也是西方形而上学的困境,而海德格尔思想作为超越形而上学的尝试,提供了一种替代方向。人们可以设想一个海德格尔式的人工智能,尽管讽刺的是,一个海德格尔式的人工智能恰恰意味着海德格尔试图摧毁的形而上学的延续。虽然把弱人工智能与从柏拉图到莱布尼茨的哲学史等同起来的做法,有时略欠精细,德莱弗斯无疑表明了人们必须考察运算的本体论、认识论和心理学假设,并质疑它们的局限性和合法性。9我们可以说,德莱弗斯强调了对世界的解释学——世界是一种前结构[vorstructure],它决定了当下的意义——以及逾越[transgressions]如何相应地改变着世界本身。德莱弗斯强调了与早期人工智能的笛卡尔机械论相反的人的诠释、人的思考的递归性质。他没有讨论现代运算,但他把现代运算与联结主义[connectionism]等同。
德莱弗斯对海德格尔和人工智能的解读在今天仍然有回响,比如布莱恩·坎特威尔·史密斯[Brian Cantwell Smith]最近的作品。10Brian Cantwell Smith,The Promise of Artificial Intelligence:Reckoning and Judgment,MIT Press,2019.不过,我们必须把自己的立场与德莱弗斯区分开,因为作为整体的世界是不可计算的,它已经处在计算的思维能力之外。我们要认识到,除了德莱弗斯对海德格尔的认知主义解读,还有另一种处理世界的方式。可以说,德莱弗斯的智能概念仍然属于海德格尔在《存在与时间》中概述的“对世界的现象学理解”的范围内。而海德格尔朝存在及其历史的转向,标志着他的哲学的转向[Kehre],这超出了德莱弗斯对人工智能的解读。在海德格尔的《对哲学的贡献》[Beiträge zur Philosophie(Vom Ereignis)]一书中,他指出《存在与时间》是朝转向的过渡;这一过渡也是从对世界的现象学解释到对未知的合理化的转变(在这里,未知是存在,是敞开性,是最后之神)。如果以这种方式解读《存在与时间》,那么我们便能明白:任何想完全模仿人类智能的机器都不能把智能限制于两种活动,比如机械的活动和有机的活动,因为这样便忽略了意义并非存在者的属性,它的深度来自无根基之物。
我们已经看到递归性是运算的基础,且世界也是递归的,但这不意味着世界是可运算的或不可运算的。在海德格尔的意义上,当我们的环境变得可运算或不可运算,世界就被抛弃了。海德格尔描述的世界从一开始就是认知的他者,它不可还原为认知,因为是世界使认知成为可能。我们可以用格式塔理论中背景与图形的关系,来理解世界与认知。世界是由指示的复杂全体构成的,认知要依赖这些指示来推理。换句话说,认知是世界的一部分,如部分与整体。然而——这也是重新解读《存在与时间》第17、18 章的关键所在——世界已不再是海德格尔所描述的现象学世界,而是一个日益被移动设备和传感器捕捉、重构的世界。这个世界很大程度上是显示在屏幕上的,尤其当我们想到今天的人几乎可以用手机应用做一切事情。智能城市、传感器和平台预设了一个完全基于可以分析、可建模的数据的世界。也就是说,随着世界成为一个技术系统,海德格尔描述的作为真理(即“无蔽”[a-letheia])基础的世界,已被简化为可用逻辑分析的数据集。
正因如此,我们觉得如今的人工智能正日益强大,海德格尔和德莱弗斯所强调世界的问题则不再重要了。我们生活在一个数字化的世界中,一个“座架”或“集置”[Gestell]的世界,人工智能的力量基于把世界简化为可运算的模型。这不是说还原论彻底是坏的,而是说将自身视为当做现实全部的还原论是坏的,18世纪的机械论的错误也在于此。随着运算性的环境取代世界,世界的不可计算性进一步远离了我们,直到问题本身也消失或灾难显现。我们只听到肯定性的技术加速、人类进步和地球工程。世界的消失开启了一种注意力的生态学,因为规定现象的显现的已不再是世界。数字时代的注意力经济学不仅是眼睛和屏幕的经济学,更重要的一点是,现象出现的相关性是由计算确定的。从社交媒体的消费推荐到政治选举中的选票操纵,随着世界越来越可计算,注意力经济变得愈发重要。当运算性环境取代了世界,并不意味着世界消失了,它只是变得沉默了。
四
我们必须把世界的递归性与技术在控制过程中的递归性区分开来;每当技术寻找背景,它就失去背景,因为技术本身渴望成为一切存在的背景。图形和背景之间的交互结构,表明了一种本体论上的拒绝,即世界不能被简化为一堆递归算法,无论这些算法在产生类似于自然的涌现方面多么强大。另一种本体论的拒绝是,可运算者同时也暗示了不可运算者,也就是说宇宙中存在不可递归枚举的存在。这两种本体论的拒绝是有区别的。仅有不可运算者还不够,因为它只是为运算设定了限度,而不能释放它的潜力。不可运算者还不是不可计算者。不可运算者只是对可运算者的否定,而不可计算者是对无根基的根基/背景[ground]的肯定。不可计算者不能被还原为不可运算者,尽管后者可以为前者提供在可运算领域之外的“理性主义”支撑。
我们的问题是——我相信斯蒂格勒的问题也在于此——如何把不可计算者整合进运算性之中,这不是说要让不可计算者变得可被运算,而是呼吁一种新的认识论和知识观,我称之为未知的认识论[epistemology of the Unknown]。我将在我的新书Art and Cosmotechnics(《艺术与宇宙技术》)11Yuk Hui,Art and Cosmotechnics,University of Minnesota Press,forthcoming 2021.中详细讨论这一点。不可计算者具体表现在我们刚才讨论的世界的问题中。它并不神秘,而是具体[konkret]、有效的[wirklich]。不可计算者不仅服务于精神和宗教目的,它也是一切超越可计算性的经济和政治的核心。它可以在精神经济或力比多经济中发挥具体的功能——我相信这种功能也是斯蒂格勒试图实现的,我们需要进一步发展它。

