几类新的集值压缩映射的FG-耦合不动点

杨红珍

(西华师范大学数学与信息学院，四川南充 637009)

0 引言

设X是任一非空集合，本文考虑(q1,q2)-拟度量空间(X,dX)，(q1,q2)-广义三角不等式为

dX(x,z)q1dX(x,y)+q2dX(y,z),q1,q2>0,∀x,y,z∈X.

(1)

在[1-3]等文献中有(q1,q2)-拟度量空间的概念及性质介绍.当q1=q2=1时，(q1,q2)-广义三角不等式转化为普通三角不等式，若dX还满足恒等性和对称性，则称(X,dX)为度量空间.2010年，Ioffe[4]研究了度量空间中耦合不动点的存在性，即存在点(ξ,η)∈X×Y，集值映射F:X→Y，G:Y→X，若η∈F(ξ)，ξ∈G(η)，则称点(ξ,η)是F和G的耦合不动点.之后，Ioffe[5,6]继续研究了度量空间中集值映射耦合不动点的存在性.2015年，Arutyunov，Avakov和Zhukovskiy[7]给出了度量空间中两个集值映射耦合不动点存在的充分条件.注意到，若ξ是F°G的不动点，η是G°F的不动点，则(ξ,η)是F和G的耦合不动点.定义F-1:Y→X是集值映射F:X→Y的逆映射，其中F-1(y):={x∈X:y∈F(x)}.当映射F(或G)的逆存在时，若G=F-1(或F=G-1)，则耦合不动点可以转化为不动点.由耦合不动点的定义知，当映射F(或G)的逆存在时，若η∈F(ξ)，ξ∈G(η)，则ξ∈F-1(η)∩G(η)(或η∈F(ξ)∩G-1(ξ))，即耦合不动点转化为重合点.2017年，刘丽亚和谷峰[8]研究了耦合重合点和耦合公共不动点，其中单值映射满足平方型压缩条件.最近，在锥度量空间和偏序度量空间中[9-11]，单值映射满足适当的压缩条件，存在唯一的FG-耦合不动点.鉴于以上结果，本文对文献[8-11]的压缩条件进行了推广，在(q1,q2)-拟度量空间中，集值映射满足几类新的压缩条件，证明了FG-耦合不动点的存在性.

1 预备知识

本文所需的符号说明及定义：设Ν是正实数集，R+是非负实数集，R++是正实数集，X是任一非空集合.称函数dX:X×X→R+是X上的度量，若对任意x,y,z∈X下列条件成立：

(i)dX(x,y)=0⟺x=y，(恒等性)；

(ii)dX(x,y)=dX(y,x)，(对称性)；

(iii)dX(x,z)dX(x,y)+dX(y,z)，(三角不等式)，

称dX为X上的度量，(X,dX)为度量空间.

定义1[3]设X是任一非空集合且q1,q2∈R++.若(1)式成立且函数dX:X×X→R+满足恒等性条件，则称dX是(q1,q2)-拟度量，(X,dX)是(q1,q2)-拟度量空间.

注1当q1=q2≥1时，称(X,dX)是拟度量空间.当q1=q2=1时，称(X,dX)是度量空间.在文献[12,13]中，f-三角不等式为dX(x,z)f(dX(x,y),dX(y,z)), ∀x,y,z∈X，其中f:R+×R+→R+满足当(r1,r2)→(0,0)时，有f(r1,r2)→0.当f(r1,r2)=q1r1+q2r2时，f-拟度量空间是(q1,q2)-拟度量空间.

定义2[3]设(X,dX)是(q1,q2)-拟度量空间，{xn}n∈Ν是X的序列，若对任意的ε∈R++，存在Ν=Νε，使得对任意的m>n>Νε有dX(xn,xm)<ε，则称{xn}n∈Ν是柯西列(或基本列).若(q1,q2)-拟度量空间的每一个柯西列都收敛于X中点，则称(X,dX)是完备的(q1,q2)-拟度量空间.

给定任意集合A,B⊆X，定义H(A,B):=max{ed(A,B),ed(B,A)}，ed(A,B):=sup{Dd(a,B),a∈A}，Dd(a,B):=inf{dX(a,b),b∈B}.称H是由(q1,q2)-拟度量dX诱导的Hausdorff度量.特别地，对任意点x∈X和集合B⊆X，定义ed(Φ,B):=0和Dd(x,Φ):=+.

定义3设(X,dX)是度量空间，F:X×X→X是集值映射，若存在(x,y)∈X×X， 使得x∈F(x,y)，

y∈F(y,x)，则称(x,y)为F的耦合不动点.

定义4设(X,dX)和(Y,dY)是两个度量空间，F:X×Y→X和G:Y×X→Y是两个集值映射，若存在(x,y)∈X×Y，使得x∈F(x,y)，y∈G(y,x)，则称(x,y)为FG-耦合不动点.

2 主要部分

定理1设(X,dX)和(Y,dY)分别是完备的(q1,q2)-拟度量空间和(ρ1,ρ2)-拟度量空间，其中

q1,q2,ρ1,ρ2≥1.F:X×Y→X和G:Y×X→Y是两个集值映射，对任意(x,y),(u,v)∈X×Y，满足下列压缩条件：

edX(F(x,y),F(u,v))kdX(x,u)+l1DdX(x,F(x,y))+l2DdX(u,F(u,v))+l3DdX(x,F(u,v))+l4DdX(u,F(x,y))，(2)

edY(G(y,x),G(v,u))

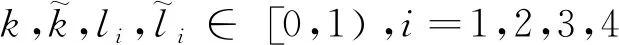
证明任取(x0,y0)∈X×Y，满足存在xn+1∈F(xn,yn)，yn+1∈G(yn,xn)，n∈Ν使得

dX(xn,xn+1)=DdX(xn,F(xn,yn)) ,dY(yn,yn+1)=DdY(yn,G(yn,xn)).

(3)

由xn∈F(xn-1,yn-1)，xn+1∈F(xn,yn)和压缩条件(2)可得，

将(3)代入上式，化简得到，

dX(xn,xn+1)kdX(xn-1,xn)+l1dX(xn-1,xn)+l2dX(xn,xn+1)+l3dX(xn-1,xn+1).

(4)

由1-l2q2-l3q2>0知1-l2>0.由(1)和(4)可得，dX(xn,xn+1)MdX(xn-1,xn)…MndX(x0,x1)，其中

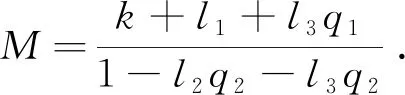
dX(x,s)q1dX(x,xn)+q2dX(xn,s),∀s∈F(x,y).

(5)

上式两边同时取下确界，再由xn∈F(xn-1,yn-1)和压缩条件(2)得，

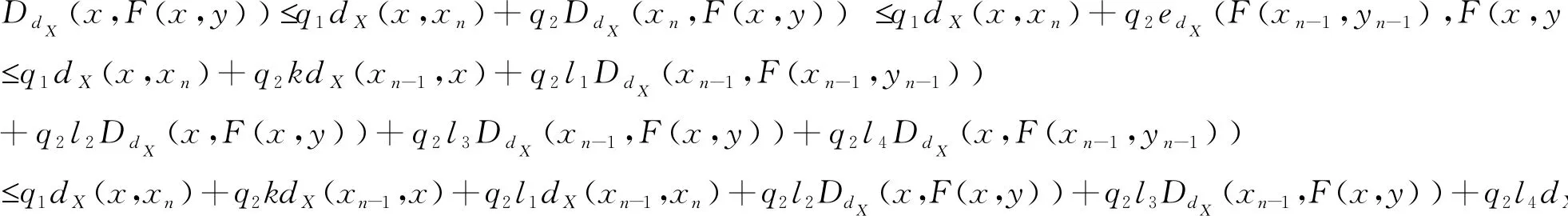
对上式取极限可得，(1-l1q2-l3q2)·DdX(x,F(x,y))0.因为1-l1q2-l3q2>0，所以DdX(x,F(x,y))=0，即x∈F(x,y).同理可得y∈G(y,x).

注2若(q1,q2)-拟度量空间是锥度量空间，F、G是单值映射，k=0,l1=l2,l3=l4，定理1退化为文献[11]中的定理1；若(q1,q2)-拟度量空间是锥度量空间，F、G是单值映射，l1=l2,l3=l4，定理1退化为文献[11]中的定理2.

定理2设(X,dX)和(Y,dY)分别是完备的(q1,q2)-拟度量空间和(ρ1,ρ2)-拟度量空间，其中

q1,q2,ρ1,ρ2≥1.令pi=max{qi,ρi},i=1,2.F:X×Y→X和G:Y×X→Y是两个集值映射，对任意

(x,y),(u,v)∈X×Y，满足下列压缩条件：

edX(F(x,y),F(u,v))k1dX(x,u)+k2dY(y,v)+l1DdX(x,F(x,y))+l2DdX(u,F(u,v))+l3DdX(x,F(u,v))+l4DdX(u,F(x,y))，

(6)

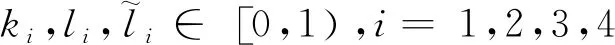
p2M∈[0,1)，其中

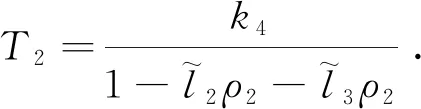
证明任取(x0,y0)∈X×Y，满足存在xn+1∈F(xn,yn)，yn+1∈G(yn,xn)，n∈Ν使得(3)成立.由定理1和压缩条件(6)可得，

同定理1, 可得

dX(xn,xn+1)M1dX(xn-1,xn)+T1dY(yn-1,yn)，

(7)

dY(yn,yn+1)M2dY(yn-1,yn)+T2dX(xn-1,xn).

(8)

将(7)和(8)相加可得

dX(xn,xn+1)+dY(yn,yn+1)(M1+T2)dX(xn-1,xn)+(M2+T1)dY(yn-1,yn)Mn(dX(x0,x1)+dY(y0,y1)).

因为p2M∈[0,1)，所以M∈[0,1).任意n∈Ν，当m>n>Ν时，由(1)知

对上式取极限得DdX(x,F(x,y))=0，即x∈F(x,y).同理，y∈G(y,x).

注3当k2=k3=0时，定理2退化为定理1.

定理3设(X,dX)和(Y,dY)分别是完备的(q1,q2)-拟度量空间和(ρ1,ρ2)-拟度量空间，其中

q1,q2,ρ1,ρ2≥1.F:X×Y→X和G:Y×X→Y是两个集值映射，对任意(x,y),(u,v)∈X×Y，满足下列压缩条件：

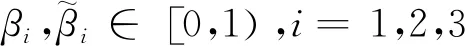
证明任取(x0,y0)∈X×Y，满足存在xn+1∈F(xn,yn)，yn+1∈G(yn,xn)，n∈Ν使得(3)成立.因为

(11)

将(3)代入(11)式后移项化简得，dX2(xn,xn+1)MdX2(xn-1,xn)…MndX2(x0,x1)，其中任意n∈Ν，当m>n>Ν时，

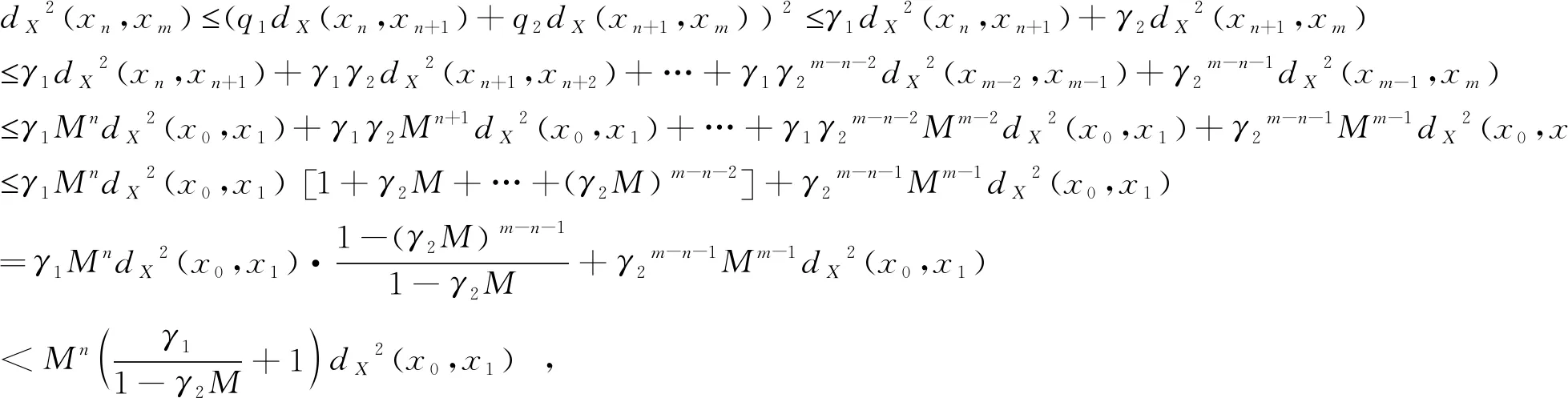
当n→时，上式右边极限为0，即DdX(x,F(x,y))=0，故x∈F(x,y).同理可得y∈G(y,x).

注4若(q1,q2)-拟度量空间是2-距离空间，F、G是单值映射且F=G，X=Y，(9)和(10)相加的结果与[8]中压缩类型类似.

3 结语

不动点理论是非线性泛函分析的重要组成部分.本文在完备的(q1,q2)-拟度量空间中，首先，对文献[11]中的压缩条件进行了扩展，介绍了两类新的集值压缩映射，这两类映射存在FG-耦合不动点定理.接着，对文献[8]中的压缩条件进行了推广，得到一类新的平方型压缩映射，并存在FG-耦合不动点定理.