基于层次分析法的大型游乐设施安全评估

余 珂，黄 晖，张静楷

（广东省特种设备检测研究院中山检测院，广东中山 528400）

0 引言

随着人们生活水平的日渐提高，大型游乐设施也日益普及，其安全问题也越来越突出[1-3]。因此，充分了解大型游乐设施的安全状况，并及时采取措施消除安全隐患，具有重大的社会价值。近年来大型游乐设施的安全评估也得到越来越多的重视[4-14]。林伟明等[15]提出了一种考虑设计、制造、安装、运行、监测和维护的大型游乐设施多级综合安全评估指标体系。王雪颖等[10]建立了大型游乐设施安全评估二级指标体系，并用专家评判法确定了各个指标的权值，实现对大型游乐设施的安全评估。庄春吉等[8]从人-机-环境-管理等4个角度出发，建立了大型游乐设施三级评估指标体系，并采用层次分析法来确定指标的权值。

大型游乐设施的安全评估，不仅需要有科学全面的安全评估指标体系，而且需要合理地确定各个指标的权值。安全评估指标体系是对安全影响因素的系统系描述，基于对设备和管理等方面的经验，可以比较准确地把握绝大部分的评价指标。权值的定义方法通常有定性的专家评判法、定量的主成分分析法、定性定量相结合的层次分析法。层次分析法通过对比同一级的评价指标相对于上一级评价指标的优劣程度来确定各个指标的权值，兼具定性分析和定量分析的优点，在复杂系统的安全评估中应用广泛[8，15，16]。但应用层次分析法进行安全评估时，需要进行一致性检验和权值调整，若同一级的评价指标较多，评价矩阵比较大，权值的调整比较繁琐。寻找简单实用的权值调整方法，将更有利于将层次分析法应用于大型系统的安全评估中。

有鉴于此，本文提出了一种随机筛选和微量调整的权值调整方法。当需要进行权值调整时，从评价矩阵中随机选取一个或多个指标，将选定的指标权值进行微调，重新进行一致性检验，不断迭代直到满足条件为止。将所提出的权值调整方法编码实现，从而可快速调整权值。以某在役观览车为例，用层次分析法确定各个指标的权值，对在役观览车进行安全评估，从而验证了所提出方法的有效性。

1 层次分析法

层次分析法针对安全评估指标体系中同一级的指标进行权值的计算。假设在某一个安全评估指标体系中，第i级指标的指标集有n个指标：

层次分析法的第一步，就是定义同一级指标的相对重要性。指标的相对重要性通常采用1-9标度法来定义，如表1所示。根据1-9标度法，可以根据经验给出当前指标集的权值矩阵：显然，矩阵Ai是对称阵，元素均大于零且对角元素均为1。

层次分析法的第二步，是计算矩阵Ai的最大特征值和对应的特征向量。经计算可得最大特征值为λmax，对应的特征向量为

层次分析法的第三步，是进行一致性检验。一致性检验的目的，是检验评判者对多指标进行评判时是否保持评判标准的一致性[16]。当完全保持一致时，有λmax=n，其余特征值均为0。但通常只要满足如下关系式即可：

式中：CI=(λmax-n)/n；CR为平均随机一致性指标。CR的取值可参考文献[8]。

表1 1-9标度法

若不满足一致性检验条件，则需要进行权值调整。权值调整的通常方法，可以是重新确定矩阵Ai，或者调整矩阵Ai中的个别权值[8，16]。但不论采取哪种方法，都面临着调整哪些权值、如何调整权值的问题，需要足够的经验知识。若能实现权值的自动调整，则可大大降低技术门槛，促进层次分析法的应用。

2 权值调整方法

本文将指标权值的调整过程建模成一个多目标优化问题：

式中：xi为优化问题的设计变量，A(X )为权值评估矩阵，Vt为权值评估矩阵的理想特征值向量（即最大特征值等于矩阵维数，其余特征值为0），Ao为初始的权值评估矩阵，D为设计变量的可行域。由表1可知，设计变量只能在有限个数值中选取（1、3、5、7、9，及其倒数），故该问题为多目标离散优化问题。

由于权值评估矩阵是对角阵，且对角元素均为1，故设计变量应取权值评估矩阵的上三角元素或下三角元素。优化目标函数F1可以使最终的解满足一致性条件，优化目标函数F2可以使权值的调整程度最小，从而尽可能保留原有的专家经验。为求解所提出的优化问题，可以用成熟的优化算法进行求解。

3 实例验证

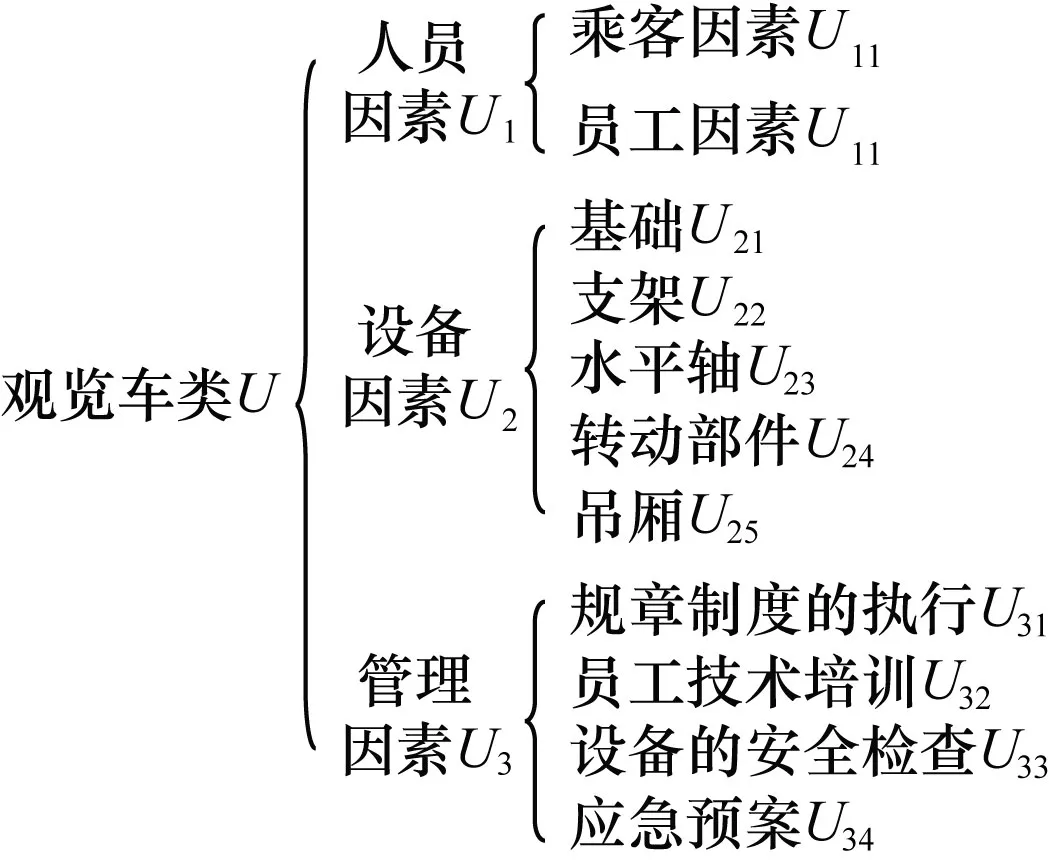
图1 在役观览车类大型游乐设施安全评估指标体系

为检验所提出的权值调整方法是否可行，本文选取某在役观览车类大型游乐设施并判断各级指标的权值。观览车类大型游乐设施的安全评估指标体系如图1所示，该安全评估指标体系同时考虑了人、设备、管理等多方面的因素，可以比较系统全面地评价在役观览车类的安全状况。由图可知，在役观览车类中设备因素U2包含了5个下一级指标。由于指标的数量比较大，权值的确定和调整比较困难，故以设备因素U2的下一级指标为例，说明用所提出的方法确定权值的基本过程。首先，根据专家经验给出一个初始的评估矩阵A（表2）。

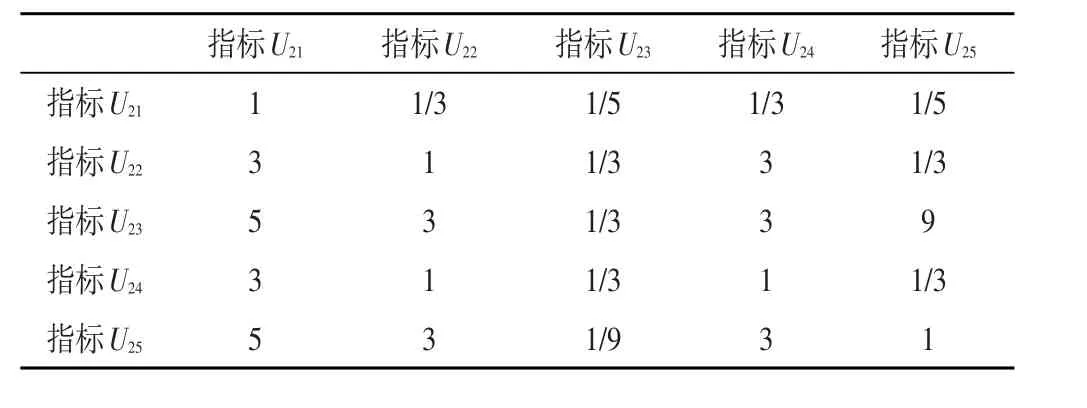
表2 设备因素的权值评估矩阵

根据层次分析法，可知最大特征值λmax=5.92，CI=( )λmax-n n=0.18，经查表可得CR=1.12，CI/CR=0.16，不满足一致性要求，需要进行优化分析。

将多目标优化问题线性加权变成单目标优化问题，并采用Matlab自带的遗传算法进行求解。最终可得既满足一致性要求、又最大程度地保留专家经验的权值评估矩阵（表3）。由修改后的权值评估矩阵，可得最大特征值λmax=5.05，CI=( )λmax-n/n=0.011，此时CI/CR=0.01，满足一致性要求。

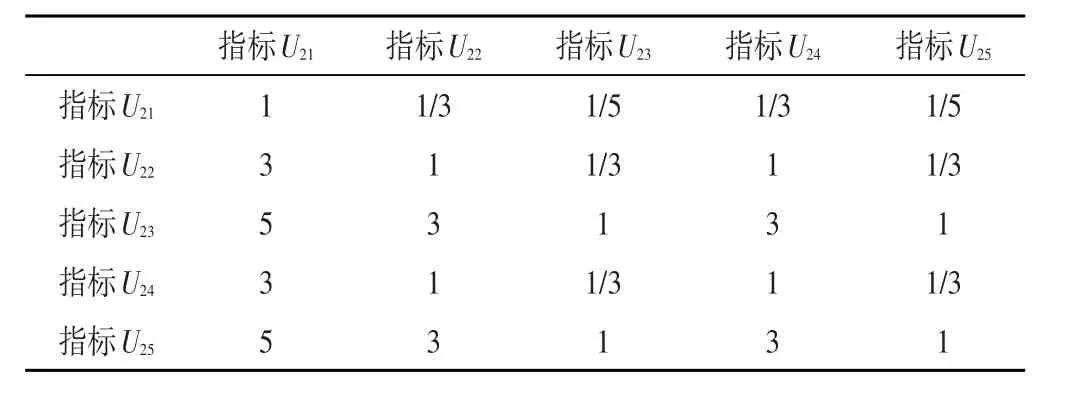
表3 调整后的设备因素的权值评估矩阵

4 结束语

层次分析法广泛应用于大型游乐设施安全评估中。但应用层次分析法评估指标权重时，需要进行一致性检验和必要的权值调整。为避免权值调整的繁琐过程，本文用优化设计的思想，将权值的调整过程建模为多目标优化问题。以在役观览车类大型游乐设施的指标权值计算为例，证明所提出的方法可实现权值的自动调整，最大程度地保留专家经验、并使权值评估尽可能地满足一致性要求。