钛合金TA16弹塑性修正因子数值分析方法研究

邵雪娇，杜 娟，杨 宇，傅孝龙，张 瀛，李 辉，郑连纲

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

在工程评价中，对于结构响应超出材料比例极限时，需进行弹塑性疲劳分析。现行核设备规范ASME[1]和RCC-M[2]中规定了两种弹塑性疲劳分析技术：一种是基于弹塑性分析的疲劳分析方法，一种是基于线弹性分析的简化弹塑性疲劳分析方法[3-4]。第1种方法需要材料的弹塑性本构模型和详细的计算历程，耗费人力和物力，在设计的初期是不切实际的。第2种方法具有效率高的特点，在工程中普遍采用[5-8]。该方法是通过弹性应变范围乘以弹塑性修正因子(KE)代替实际塑性应变范围进行疲劳评价。国内外学者在相关领域进行了大量的研究[9-11]，杜娟等[12]对钛合金TA17的弹塑性修正因子开展了材料试验和分析方法研究，给出了TA17的KE相关系数。现行核设备规范ASME或RCC-M中给出了常用材料的KE表达式和系数，但缺少钛合金TA16所需的KE表达式和相关系数，无法开展TA16设备的简化弹塑性疲劳分析。同时也缺少TA16弹塑性疲劳分析所需循环弹塑性本构模型，使得开展相关TA16疲劳弹塑性技术试验与分析研究工作非常迫切。

本文通过理论分析，采用数值分析方法获取规范外材料TA16的KE通用表达式及相关系数，为开展TA16简化弹塑性疲劳分析奠定基础。

1 试验及本构模型

1.1 TA16循环变形试验

对TA16薄壁圆管进行常温和高温下的单轴拉伸试验、应变循环试验和应力循环试验，结果如图1、2所示。由图1可看出，TA16在350 ℃下单轴拉伸曲线比稳定循环应力应变曲线稍低。由图2可看出：TA16在30 ℃和350 ℃下产生明显的棘轮行为，峰谷值应变随循环周次的增加而增加，由于材料的循环稳定特性，其增加率近似为常数。钛合金应用到蒸汽机发生器中将承受循环热载荷作用，材料不可避免会产生棘轮行为，材料在局部高应力区将发生塑性应变的循环累积，从而导致材料宏观尺寸变化，进而影响结构的使用寿命。因此，在钛合金的结构设计中必须合理考虑其棘轮行为的影响。

a——30 ℃下循环应力应变曲线；b——30 ℃下稳定循环应力应变曲线和单轴拉伸曲线对比；c——350 ℃下循环应力应变曲线；d——350 ℃下稳定循环应力应变曲线和单轴拉伸曲线对比图1 TA16在不同应变幅值下的试验结果Fig.1 Test result of TA16 with different strain amplifies

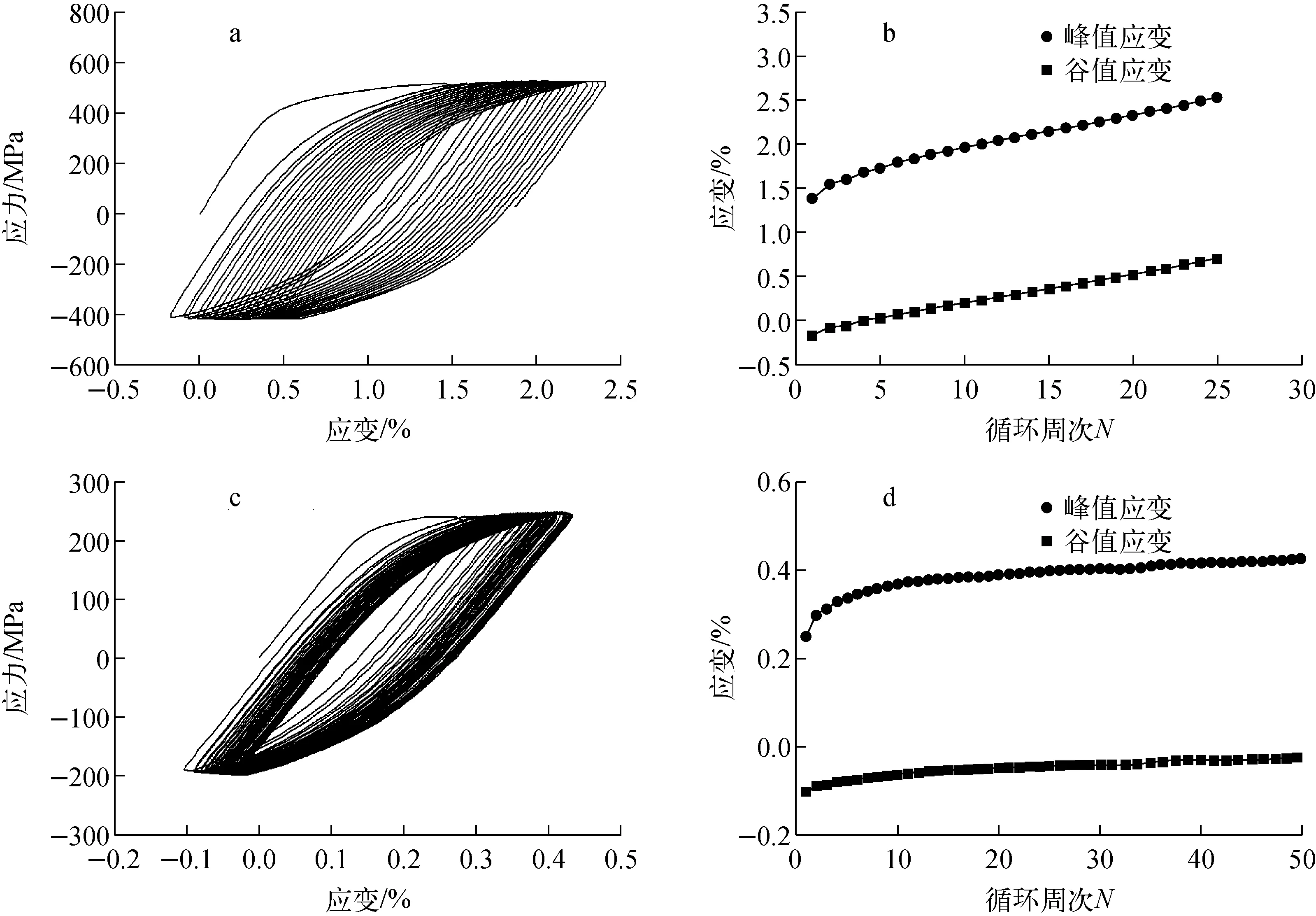
a——30 ℃下滞回环曲线；b——30 ℃下峰谷值应变随循环周次的变化；c——350 ℃下滞回环曲线；d——350 ℃下峰谷值应变随循环周次的变化应力控制：a、b——50 MPa±450 MPa；c、d——25 MPa±225 MPa图2 TA16应力控制下的循环应力应变曲线Fig.2 Cyclic stress-strain curve of TA16 under stress control

1.2 本构模型的确定

基于规范所提供的不锈钢材料Z2CND18.12(控氮)的参数和TA16的循环变形试验，采用多线性弹塑性本构模型(EP本构模型)和Chaboche等[13]非线性随动硬化本构模型(Chaboche本构模型)[14-15]对TA16的单轴拉伸曲线进行模拟，模拟结果如图3所示。从图3可看出，两种本构模型的模拟结果均与试验结果较吻合。Chaboche本构模型已被嵌入到大型有限元软件ANSYS的材料库中，用于描述材料在应力应变循环中随动硬化变形行为，其背应力演化方程[13]为：

(1)

(2)

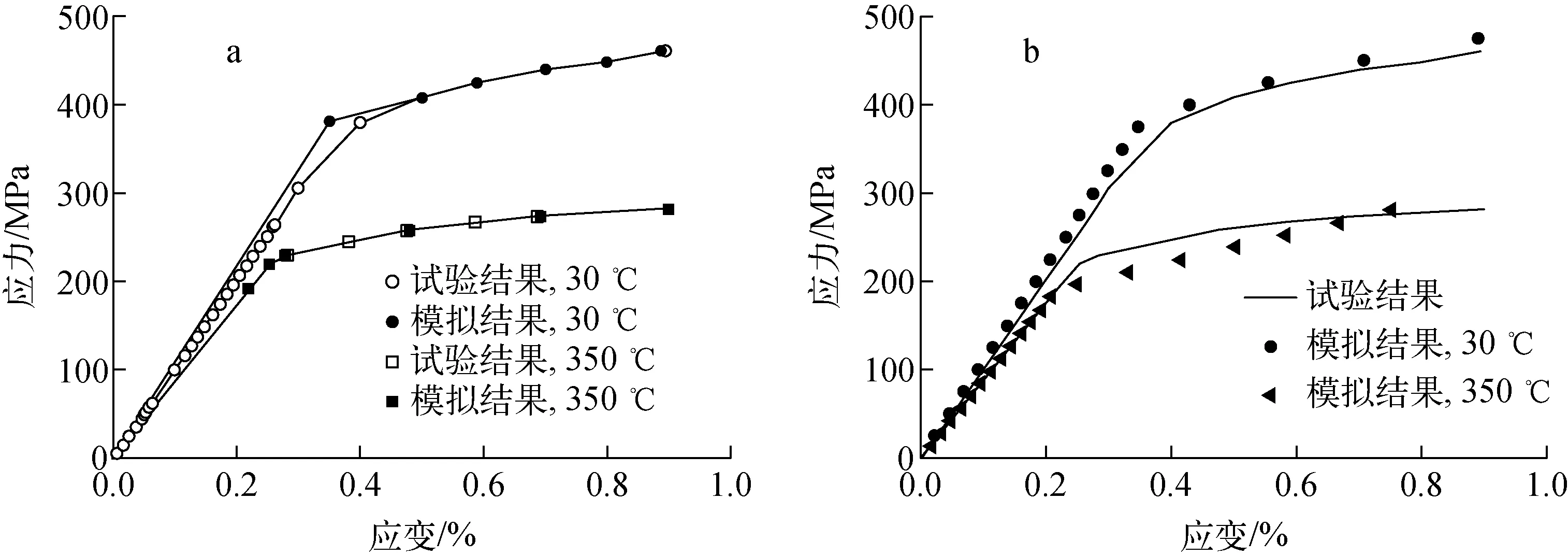
a——EP本构模型；b——Chaboche本构模型图3 不同温度下TA16的试验结果和ANSYS模拟结果Fig.3 Test and ANSYS simulation results of TA16 at different temperatures

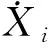
ci和γi由应变控制、不同温度下的稳定循环应力应变曲线通过最小二乘法拟合获得，Chaboche本构模型参数列于表1。

表1 TA16的Chaboche本构模型材料参数Table 1 Parameter of Chaboche constitutive model of TA16

2 KE的数值分析方法

KE表示弹塑性分析得到的弹塑性应变范围与弹性分析得到的等效弹性应变范围的比值。在进行简化弹塑性疲劳分析时，对于机械载荷作用的情形，RCC-M规范根据一次加二次应力范围Sn采用式(3)[2]计算简化弹塑性疲劳分析的关键系数KEmech。对于热和机械载荷共同作用的情形，还需采用式(4)[2]计算热载荷作用下的KEtherm，再通过式(5)[2]得到总的弹塑性修正因子KERCC-M。

(3)

(4)

(5)

其中：m、n、A、B、C为与材料相关的系数，n为材料硬化指数；Sm为许用应力强度；Sp(meca)为机械载荷计算的总体应力幅值；Sp(therm)为热载荷计算的总体应力幅值；Sp(total)为机械载荷加热载荷计算的总体应力幅值。对于奥氏体不锈钢，m=1.7，n=0.3，A=1.86，B=1.66，C=1.86。

图4示出利用弹性分析和弹塑性分析得到的KEEP与KERCC-M的包络关系。由图4可见，当Sn遍布于3Sm～3mSm的区间内，通过弹性分析和弹塑性分析得到的KEEP应位于规范规定的简化弹塑性分析方法获取的KERCC-M下方(图4所示的阴影区域)，即KERCC-M应为KEEP的包络值。为全面分析KE的影响因素，考虑了4种敏感因素，包括加载方式、本构模型、载荷类型和材料温度。加载方式采用位移载荷和力载荷两种方式；本构模型采用EP本构模型和Chaboche本构模型；载荷类型选取了热载荷、机械载荷及热-机械载荷共同作用的方式；材料温度选取30 ℃和350 ℃两种温度。

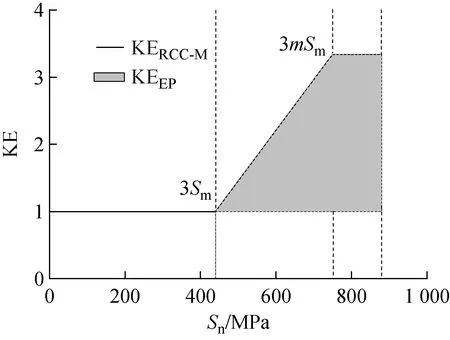
图4 KEEP与KERCC-M的包络关系Fig.4 Envelope relationship of KEEP and KERCC-M

有限元分析模型采用具有代表性的缺口薄板和接管嘴过渡段，如图5所示。为使得到Sn分布在规范关心的区间(3Sm～3mSm)内，需调整模型的几何形状，改变模型的应力集中程度。缺口薄板中L为长度，H为高度，B为壁厚，R为缺口半径，通过调整R可改变缺口处的应力分布。接管嘴过渡段中L1、L2和L3分别为均直段和变截面处的长度，T1和T2为壁厚，L3可控制变截面的倾斜程度，从而改变截面变化处的应力分布。

Z2CND18.12(控氮)在各种敏感因素作用下的最小保守裕量如图6所示，以此作为TA16 KE表达式及其相关系数确定的依据。最小保守裕量η通过下式求得：

KERCC-M>1,Sn>3mSm

(6)

a——缺口薄板；b——接管嘴图5 有限元计算模型Fig.5 Finite element model

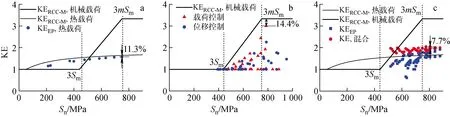
a——热载荷；b——机械载荷；c——热-机械载荷共同作用图6 Z2CND18.12(控氮)在不同Sn下的KEFig.6 KE of Z2CND18.12 (nitrogen control) under different Sn

3 TA16弹塑性修正因子数值模拟

RCC-M规范中给出了奥氏体不锈钢材料的KE表达式和相关系数，参考Z2CND18.12(控氮)的最小保守裕量，确定TA16的KE表达式和相关系数。为保证KE表达式在ANSYS软件中的适用性，对TA16采用和RCC-M规范相同的KE表达式，先假设TA16初始相关系数，如表2所列，在考虑结构、载荷、本构关系等影响因素的情况下计算出TA16的最小保守裕量，最小保守裕量需接近且略高于规范提供的奥氏体不锈钢的最小保守裕量，如果不满足要求，反复迭代修正相关系数。

表2 Z2CND18.12(控氮)和TA16的KE相关参数Table 2 Parameter of KE for Z2CND18.12 (nitrogen control) and TA16

采用缺口薄板和接管嘴的有限元模型，考虑各敏感因素计算得到TA16 KE初始参数随Sn的变化，如图7所示。由图7可看出，机械载荷和热载荷作用下的KEEP远低于按照奥氏体不锈钢给定的KE表达式及其相关系数计算得到的KERCC-M，机械载荷作用下TA16的最小保守裕量为64.7%，热载荷作用下TA16的最小保守裕量为76.1%。这表明，奥氏体不锈钢的KE表达式及其相关系数对TA16而言过于保守。主要原因在于TA16的热膨胀系数低于奥氏体不锈钢(350 ℃时约为奥氏体不锈钢的50%)和屈强比过高(室温时奥氏体不锈钢的屈强比约为0.4，而TA16的约为0.7～0.87)，因而需重新确定1组更合理的相关系数。

经过优化分析，最终确定的相关系数如表2所列，在该组参数下得到的KE结果如图8所示。由图8可知，无论是热载荷还是机械载荷，利用优化后的参数计算的KERCC-M均完全包络KEEP。TA16优化前后与Z2CND18.12(控氮)的弹塑性修正因子最小保守裕量对比列于表3。由表3可知，TA16在各种载荷类型下的最小保守裕量均满足要求，参数优化的最小保守裕量更接近且略高于RCC-M规范提供的Z2CND18.12(控氮)材料的保守裕量。

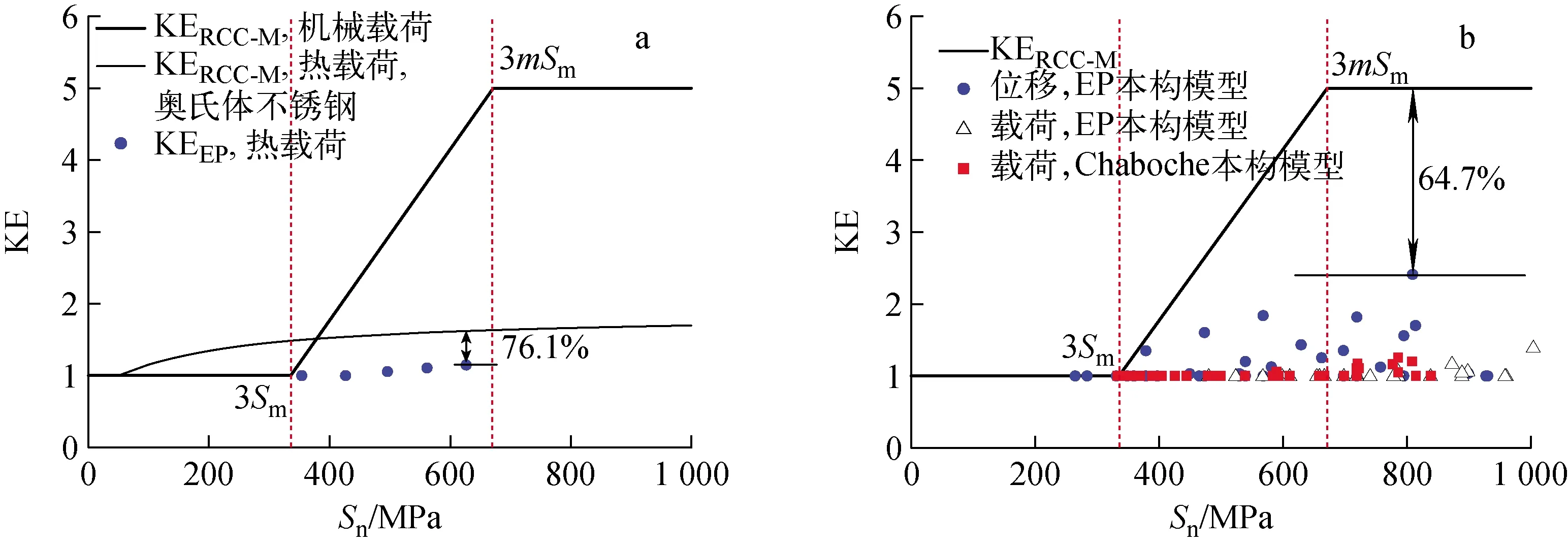
a——热载荷；b——机械载荷图7 TA16初始参数下不同Sn的KEFig.7 KE of different Sn under TA16 initial parameter

a——热载荷；b——机械载荷图8 相关参数优化后的KE随Sn的变化Fig.8 Change of KE with Sn after optimization of related parameter

表3 Z2CND18.12(控氮)和TA16的最小保守裕量Table 3 Minimum conservative margin of Z2CND18.12 (nitrogen control) and TA16

注：1) 考虑TA16材料参数的波动而增加保守量后的值(增加值为4.4%)

4 结论

1) 对钛合金TA16的单轴拉伸、应变循环和应力循环进行试验研究，获取钛合金材料循环变形特性，建立了TA16的随动硬化弹塑性本构模型。

2) 基于规范给出的奥氏体不锈钢的KE相关参数和表达式，考虑了各种敏感因素，计算出Z2CND18.12(控氮)弹性分析和弹塑性分析得出的KEEP与规范计算方法得出的KERCC-M的最小保守裕量。

3) 确定了TA16的KE的表达式和相关系数，建立了非规范材料弹塑性修正因子相关系数的数值计算方法，完善了对TA16进行疲劳分析的参数。