基于伴随粒子的快中子成像系统角分辨研究
孙世峰,欧阳晓平
(1.华北电力大学 核科学与工程学院,北京 102206;2.华北电力大学 非能动核能安全技术北京市重点实验室,北京 102206;3.西北核技术研究院 强脉冲辐射环境模拟与效应国家重点实验室,陕西 西安 710024)
伴随粒子成像技术是一种优良的快中子成像方法,它利用D-T聚变反应产生的α粒子和中子具有时间与运动方向关联这一特性,通过探测伴随α粒子来标记单能14 MeV快中子以进行成像[1-2]。与常规采用机械准直的成像技术相比,伴随粒子成像技术采用电子准直技术降低γ射线和散射中子等的干扰。成像系统不需使用外部屏蔽或准直器,极大地增强了系统的可移动性。目前,该技术已被广泛用于特殊核材料和爆炸物等的检测[3-7]。基于伴随粒子的成像系统可实现多模态成像,包括透射成像、弹性散射成像、受激裂变成像等[8]。成像系统重建图像的质量主要取决于系统的性能指标参数,包括系统的角分辨和时间分辨等,提高成像系统的角分辨和时间分辨,可增强系统解析物体的能力和重建图像的对比度[9-10]。相关研究结果表明,当系统角分辨从3°提升至1°时,重建图像的质量会明显提高[9]。成像系统的时间分辨主要由探测器的时间性能决定[11],而影响系统角分辨的因素较多。因此本文通过理论计算评估影响系统角分辨的主要因素,并采用基于GEANT4的蒙特卡罗模拟方法,定量分析不同参数下系统的角分辨,为伴随粒子成像系统的设计和研制提供参考和依据。
1 伴随粒子成像技术原理
图1为基于伴随粒子的快中子成像系统示意图,基于伴随粒子的快中子成像系统一般由3部分组成:小型密封D-T中子管、伴随α探测器和快中子探测器阵列。D-T中子管通过D-T聚变反应产生快中子,即:
(1)
其中,Q为反应所释放的能量。
对于D-T聚变反应,Q为17.589 3 MeV。在质心坐标系中,上述反应产生的α粒子(3.540 35 MeV)和快中子(14.048 9 MeV)的运动方向为180°相反。因此,伴随粒子成像系统可通过测量每个与中子相关联的α粒子,反推被标记的快中子的运动方向和起始时间。伴随α探测器是位置灵敏的探测器,实现对入射α粒子的作用位置和时间的精确测量,提供被标记中子的初始运动方向和起始时间。快中子探测器阵列记录测量到的快中子的作用点位置和时间,从而确定入射中子的运动方向和飞行时间。

图1 基于伴随粒子的快中子成像系统示意图Fig.1 Schematic of associated particle fast neutron imaging system
通过比较被标记中子和测量到的中子的运动方向和时间信息,可判定测量到的中子为直接透射中子、弹性散射中子或诱发裂变中子等。直接透射中子可通过判断是否与中子初始运动方向一致以及是否符合14 MeV中子对应的飞行时间进行识别;诱发裂变中子是通过判断在适当的飞行时间内是否存在多个同时测量到的中子事例进行识别;弹性散射中子是通过判断散射角和飞行时间与被标记中子和假定质量数的原子核发生单次弹性散射时的结果是否相一致进行识别。成像系统可实现3种模态的快中子成像,包括透射成像、弹性散射成像和受激裂变成像,详细的图像重建原理及重建算法可参考文献[8-9]。
成像系统对被测物体的检测和成像能力取决于重建图像的质量,而图像质量直接取决于系统的角分辨和时间分辨。系统的时间分辨取决于α探测器、中子探测器阵列和电子学的时间分辨率,即:
(2)
其中,σsys、σα、σn、σelec分别为系统、α探测器、中子探测器阵列及电子学的时间分辨。
而成像系统的角分辨同时受到D-T反应中入射离子的初始动量、靶点直径、中子管几何结构、α探测器和中子探测器阵列的位置分辨等多个因素的影响[12],很难用一个简单的公式描述。
2 影响角分辨的主要因素
2.1 初始动量对角分辨的影响
在质心坐标系中,D-T反应产生的α粒子和中子的运动方向为180°相反。然而,由于参与反应的D或T核的初始动量并不为0,这部分动量会被转移到反应产物,导致α粒子和中子在实验坐标系的夹角小于180°[12]。图2为α粒子和中子在质心坐标系与实验室坐标系中的出射角度,α粒子和中子分别以vα和vn的速度沿相反的方向出射,α粒子和中子的出射角与水平方向的夹角均为θ。由于入射D或T具有一定的初始动量,α粒子和中子在实验室坐标系中的出射角变为φ和ψ。设质心坐标系速度为vc,α粒子和中子在实验室坐标系中的速度为vα2和vn2,则α粒子和中子在实验室坐标系与质心坐标系中的出射角关系为:
(3)
(4)
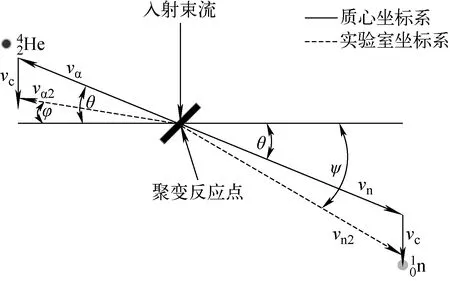
图2 α粒子和中子在质心坐标系与实验室坐标系中的出射角度Fig.2 Emission angle of alpha particle and neutron in mass center and laboratory reference frames
由式(3)~(4)可看出,实验室坐标系中出射α粒子和中子的夹角取决于质心坐标系参考角θ和初始速度vc。D-T中子管的技术方案不同,入射离子的种类和能量分布也不相同。参照一种基于射频离子源的D-T中子发生器的设计[13],假设参与聚变反应的离子仅有D+,其能量均匀分布于60~80 keV,经过计算,质心坐标系的速度为0.003 202c~0.003 698c(c为真空中的光速)。同时,由于α探测器的探测面积有限,设可测量的θ范围为-25°~+25°,按照式(3)和(4)可计算得到实验室坐标系中出射α粒子和中子的夹角。
由于入射离子具有一定的初始动量,α粒子和中子在实验室坐标系的角度与质心坐标系的角度相比均有一定的偏差(图3a)。其中,中子的偏差在1°左右,而α粒子的偏差在3.7°~4.9°。α粒子和中子在实验室坐标系中的夹角变化范围为173.9°~175.3°,最大误差为1.4°(图3b)。作为对比,若参与反应的粒子为单一能量80 keV,则α粒子和中子在实验室坐标系中的夹角变化范围为173.9°~174.6°,最大误差为0.7°。因此,由于入射离子具有一定初始动量引起的关联角不确定度小于1°,而如果入射离子具有一定的速度分布,会使关联角的不确定度增大。

图3 实验室坐标系中α粒子和中子的夹角与质心坐标系中角度的关系Fig.3 Angle between alpha and neutron in laboratory reference frame as a function of mass center frame angle
2.2 靶点直径对角分辨的影响
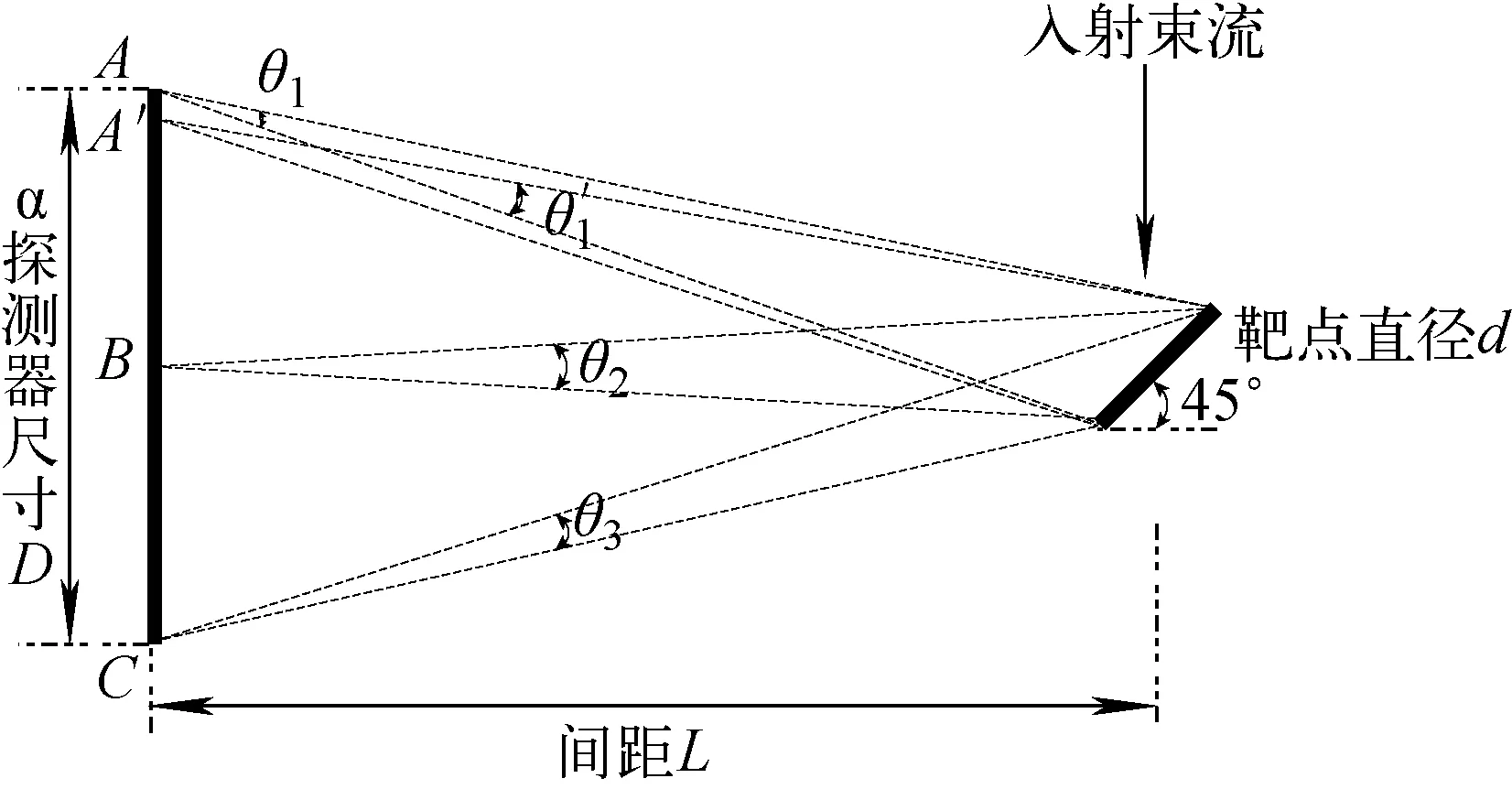
图4 由靶点尺寸引起的角分辨示意图Fig.4 Schematic of angular resolution due to D-T target spot size
实际使用的D-T中子管的靶点并不是无限小的,即D-T反应产物并非从同一个无穷小的点射出。靶点直径相对于α探测器上的任一点都有1个立体角,导致系统角分辨存在不确定度。为了使入射离子和靶上材料发生反应,同时使反应产生的α粒子能从靶上脱离并被探测到,靶安装于相对入射离子束和α探测器均为45°角的位置。由于靶点直径相对于α探测器上不同位置的点的张角不同,α探测器上不同位置的角分辨也不相同(图4)。从α探测器上边缘点A到中心点B再到下边缘点C,对应的角分辨依次减小。A点是由于靶点直径引起的角分辨,可按照式(5)计算:
(5)
其中:L为α探测器和靶中心点的间距;d为靶点直径;D为α探测器尺寸。类似地,可得到B或C点的角分辨计算公式。
设L和D分别为57.0 mm和50.0 mm,并假设α探测器具有理想的位置分辨。通过计算可得到d为不同值时α探测器上3个典型位置对应的角分辨(表1)。从表1可看出:不同位置的角分辨差异较大;随靶点直径的增大,角分辨明显变大。
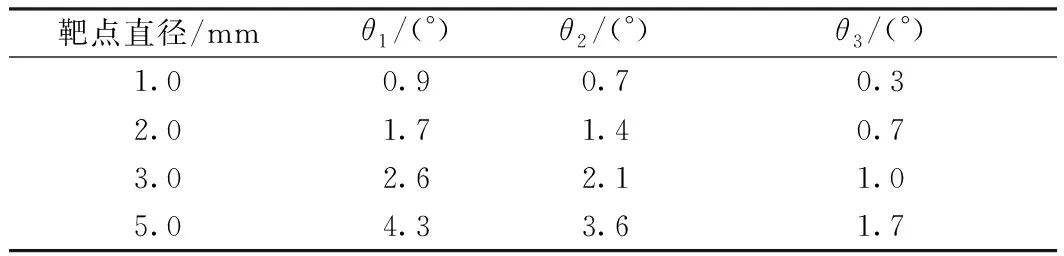
表1 α探测器上不同位置对应的角分辨Table 1 Angular resolution corresponding to different positions of alpha detector
2.3 其他影响因素
除上述两个因素外,其他影响角分辨的主要因素包括:α探测器和中子探测器阵列的空间分辨率、出射α粒子受到的干扰等。
如图4所示,实际使用的α探测器的空间分辨率为有限值,设线段AA′的长度为探测器的空间分辨率m,则A点的角分辨将从θ1增大为θ′1,其他位置对应的角分辨也有不同程度的增大。中子探测器阵列对角分辨的影响主要取决于其空间分辨率n的大小,当n较小时,其影响可忽略。如当中子探测器阵列距靶点1 m时,若n为4 mm,则单个快中子探测器像素对靶点的张角为0.23°,远小于靶点直径等的影响。
在中子管内部,存在一些其他因素可能会影响α粒子的初始运动方向,进一步增大关联角的不确定度。部分聚变反应发生于靶的内部,但由于反应产物α粒子需穿过的靶厚度较小(对于钛靶,厚度约为125 nm),其运动方向的变化可忽略[9]。但脱离靶后的α粒子可能与中子管内其他粒子发生碰撞或受磁场的影响,运动方向发生较大偏移[14]。优化中子管设计及制造工艺,可减小此因素的影响。
3 角分辨模拟计算与分析
3.1 基于GEANT4的模拟计算
本工作设计了基于GEANT4的模拟程序,计算不同参数下系统的角分辨。根据图4做如下建模:α探测器的材料为ZnO:Ga闪烁体,有效面积为50.0 mm×50.0 mm,厚度为0.5 mm。α探测器中心和靶点中心间距为57.0 mm。靶点设为一个相对于α探测器倾斜角为45°的圆盘,直径从1.0 mm至5.0 mm变化。模拟计算时,对每个事例,先从靶点范围内随机选取1个点作为粒子发射的起始点,再从质心坐标系中随机选取1个方向,发射1个能量3.5 MeV的α粒子,同时发射1个与α粒子方向相反的能量14 MeV的中子。质心坐标系的速度为固定值0.003 698c或在0.003 202c~0.003 698c范围内随机选取,α粒子和中子在实验室坐标系中的出射方向根据式(3)、(4)计算。模拟程序记录每个事例对应的中子出射角度、α粒子在闪烁体上作用点位置和沉积能量等信息。每次模拟的总粒子数相同,均为1×1011。
3.2 模拟结果分析
对于记录的原始模拟数据,根据α粒子在探测器上的作用点位置和被标记中子的出射角,计算得到不同α探测器分辨率时对应的中子出射角分布。图5、6分别为靶点直径为1.0 mm、2.0 mm,α探测器具有不同空间分辨率
时,探测器上3个典型位置对应的被标记中子原始出射角分布的二维图像。图5、6中的中子出射角分布均为总出射中子的角分布,图像形状均为一圆形的底部和一正方形顶部,这是由于探测器像素的形状(正方形)与靶点的形状(圆形)卷积形成的。若靶点为理想的无穷小点,中子出射角分布的二维图像应为理想的矩形。α探测器上不同位置对应的中子出射角分布范围和形状均不相同。α探测器分辨越差,系统的角分辨也越差。对比图5、6可看出,随靶点直径的增大,圆形底部分布的范围也越大。探测器分辨率为0.5 mm时,对于中心位置的单位像素,靶点直径分别为1.0 mm和2.0 mm对应的角分辨(1/10高宽)分别为0.9°和1.4°。若以半高宽定义角分辨,相应的结果分别为0.5°和0.6°。
图7为不同靶点直径时α探测器中心位置对应的被标记中子出射角分布,中子出射角分布均为总出射中子的角分布。对比图5、6相同参数下的结果可知,初始动量的变化使中子出射角沿y方向的分布展宽。探测器分辨率为0.5 mm时,由于初始动量的变化,靶点直径为1.0、2.0 mm时沿y方向对应的角分辨(1/10高宽)分别增大为1.4°和1.8°。若以半高宽定义角分辨,相应的结果分别为0.9°和1.0°。相比于初始动量为固定值时的结果,上述数值均明显增大。为实现高的系统角分辨,应尽可能减小入射离子的动量变化范围。
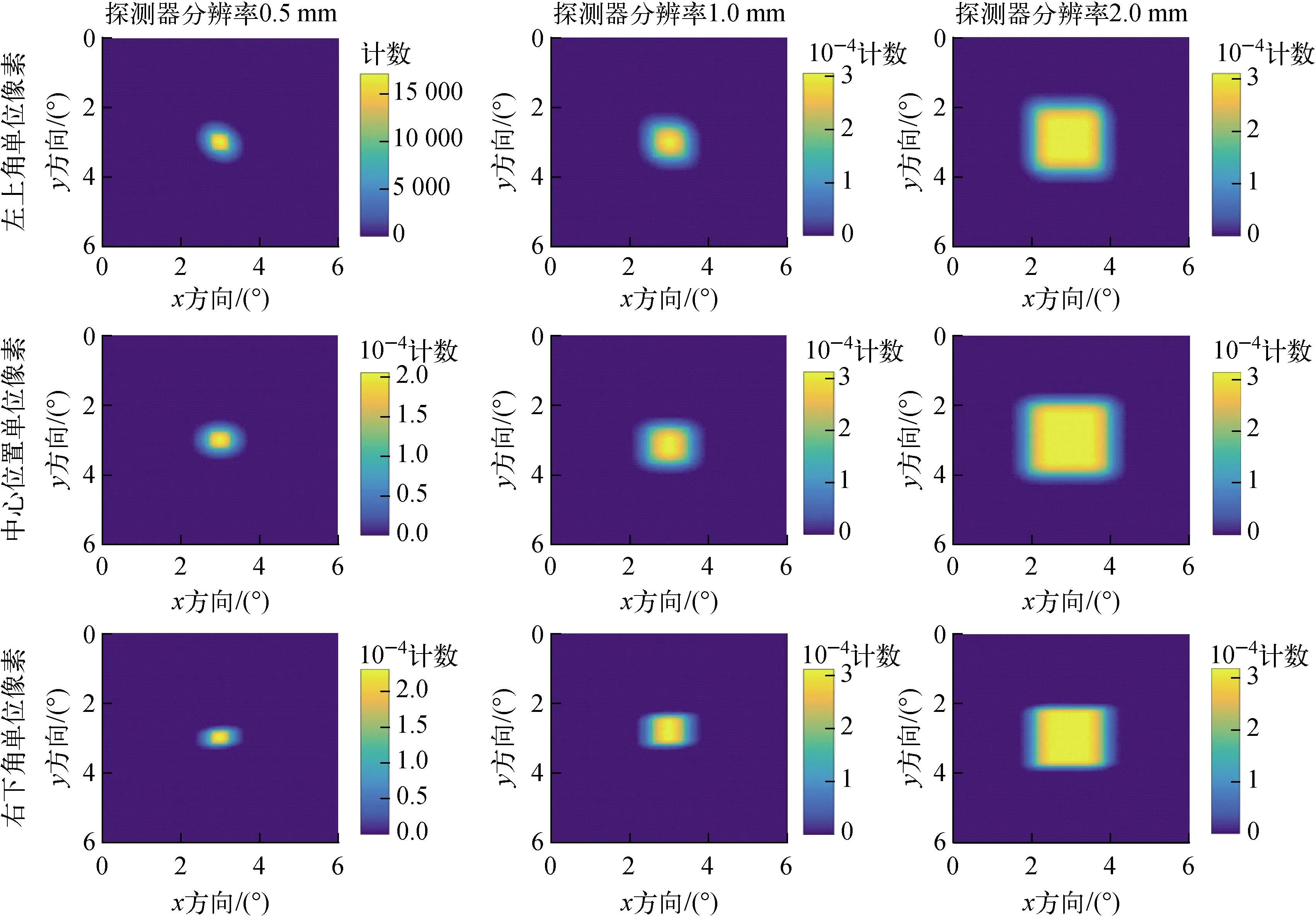
图5 靶点直径为1.0 mm时α探测器上不同位置对应的被标记中子出射角分布Fig.5 Tagged neutron emission angle distribution corresponding to different positions on alpha detector with target spot diameter of 1.0 mm

图6 靶点直径为2.0 mm时α探测器上不同位置对应的被标记中子出射角分布Fig.6 Tagged neutron emission angle distribution corresponding to different positions on alpha detector with target spot diameter of 2.0 mm
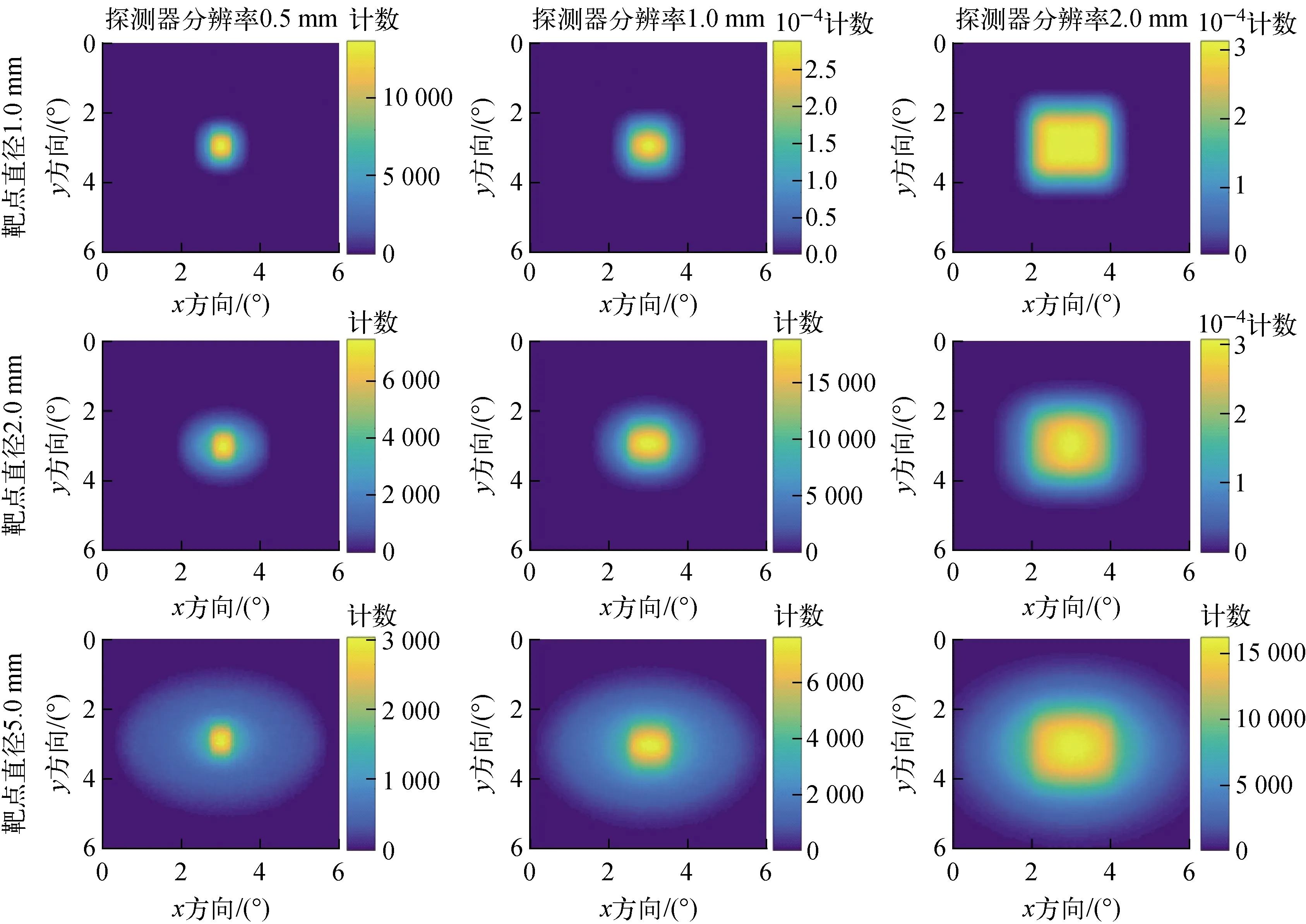
图7 不同靶点直径时α探测器中心位置对应的被标记中子出射角分布Fig.7 Tagged neutron emission angle distribution corresponding to center position of alpha detector with different target spot diameters
4 结论
本文对基于伴随粒子的快中子成像系统的角分辨进行了理论分析和模拟计算,给出了入射离子的初始动量、靶点尺寸和探测器空间分辨等对角分辨的影响,通过分析可得到如下结论:1) 受入射离子初始动量的影响,α粒子和中子在实验室坐标系中的夹角小于180°,初始动量的变化会增大角分辨;2) α探测器上不同位置对应的角分辨不同,靶点直径越大,角分辨越大;3) 探测器空间分辨率越大,角分辨越大。基于GEANT4的模拟计算结果显示,当α探测器分辨率优于0.5 mm时,角分辨主要受靶点直径影响。当系统角分辨较小时,参与反应的粒子初始动量的变化对角分辨的影响不可忽略。若要求角分辨小于1°,靶点直径需小于1 mm,α探测器的空间分辨率需小于0.5 mm。

