空间效应模型在青贮玉米新品系评比试验中的应用

焦金龙，向海游，杨子和，赵 丽，张艳茹，王 伟，吴元奇*

（1.四川农业大学玉米研究所，成都 611130；2.四川农业大学农学院，成都 611130）

农作物新品种培育需要进行品种比较试验，田间试验常受两类变异因素的影响，即空间差异和随机误差[1]。田间试验存在空间上的差异性，是由试验田地理位置、土壤结构、施肥情况[2]、营养成分[3]及一些病虫害等因素引起[4]，这会对田间试验造成极大的影响。随机误差由处理和区组的交互作用引起，而与小区地理位置无关[5]。新品种评比试验中，育种家通常采用间比法随机区组设计进行田间试验[6-7]，采用传统方差分析进行结果分析。而在实际试验中要保证区组内试验条件的均匀性很难完成，这是一种很普遍的现象。而传统方差分析方法难以有效控制田间试验中的空间变异，导致试验结果产生较大偏差。

近年来，随着数据分析软件的不断完善和推广，国内外学者提出了用空间效应模型对田间数据进行分析，该方法基于地理统计学处理空间变异的原理，是利用小区所处的空间位置，结合空间效应模型，通过空间协方差反映试验小区空间变异的特性，将变异特性与混合线性模型相结合应用于试验误差的矫正达到对空间变异的控制[8]。空间效应模型相比于传统的方差分析，仅需对试验小区的地理位置编号，即可进行数据分析，复杂的运算可以通过相关的程序分析软件进行，操作简单方便，在试验地土壤肥力存在差异时其分析结果可靠性高[9]。目前，国内很少有人将空间模型应用在青贮玉米评比试验分析中。

本试验基于统计分析SAS软件，利用混合效应模型（proc mixed）过程对青贮玉米品种评比试验数据进行空间模型分析和传统方差分析[10]，比较数据的拟合效果、效应误差估计、效应估计和效应显著性差异，从而确定空间模型和传统方差分析的差异，以及空间模型在田间数据分析中的准确性及对田间空间差异的控制。综上所述，本试验的目的：在试验设计条件为非标准随机区组设计时，研究空间模型分析是否适用于青贮品系比较，为模型的合理应用提供理论依据。

1 材料和方法

1.1 试验材料

四川农业大学玉米研究所提供的22个待评比的青贮玉米品系，对照为雅玉青贮8号，品系及田间编号见表1。

表1 亲本组合或品系名称对应编号Table 1 Parent combination or Lines name corresponding number

1.2 试验设计

于2018年3—8月在四川农业大学崇州实验基地进行试验。根据崇州试验地和供试品系的数量，采取遵循重复、随机区组排列、局部控制的原则下，进行随机区组设计划分为8个区组，每个区组小区数量不一，共种植23个青贮玉米品系，设置两次重复。于2018年3月23日播种，各品系分别种植15行，行距为0.75 m，每行12穴，每穴3粒种子，种植密度为62 900株/hm2，设保护行。根据所建立直角坐标系设定坐标原点为（0，0），计算出每个小区中心位置坐标（X，Y），坐标具体数值见附表2。

1.2 测定指标和方法

生物产量的计算：全株含水量60%～70%时，即在籽粒乳线中期至蜡熟期之前（即籽粒1/4乳线和3/4乳线之间）收获，记录各小区总株数和总鲜重。平均单株鲜重为测量小区总鲜重除以测量小区总株数。

1.3 数据分析

采用方差分析模型[11-12]和空间效应模型[13]分别分析。

方差分析模型表示为：

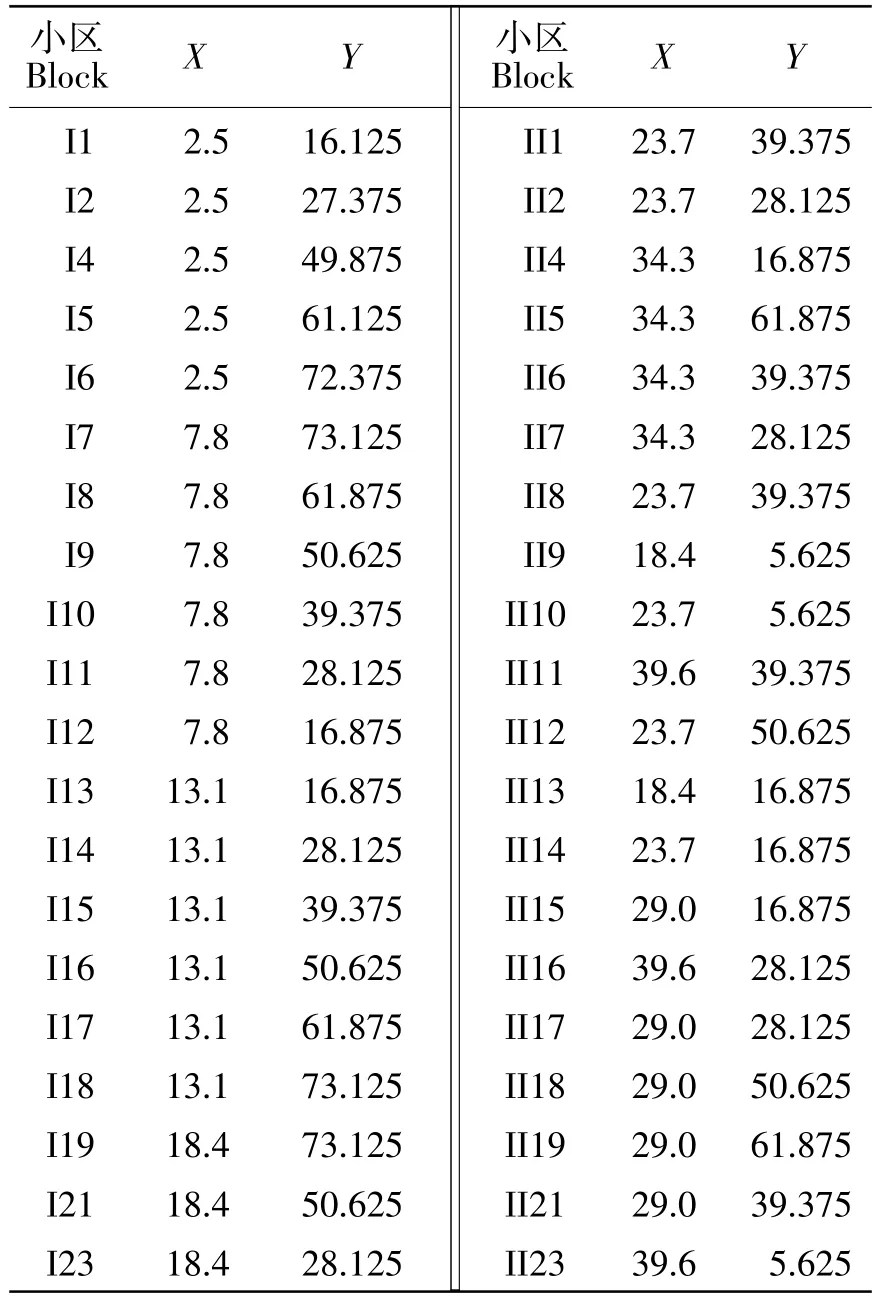
表2 试验小区坐标Table 2 Coordinates of test plot

空间效应模型表示为：

模型（1）中，μ 为总体均值，gi为品种效应，blj为区组效应，eij为剩余误差，模型（2）中与模型（1）各部分基本相同，剩余误差的分布在 eij～N[o，C（h）]，C（h）表示距离为h的两小区之间剩余误差间的方差-协方差。若以es和es+h分别表示二小区距离为h的小区剩余误差，则 C（h）定义为[14]：

其中σ02和σ2表示随机性和结构性误差方差组分，两者之和组成剩余误差的方差；σ2[f（h）]表示剩余误差的协方差，表明两个剩余误差之间的协方差是其所在小区间距离的函数。不同的空间变异表现在[f（h）]的形式（空间效应模型）及其参数不同。田间试验中常会遇到且在SAS软件中可供选择使用的[f（h）]形式，有指数模型（Exponential model）、球状模型（Spherical model）、高斯模型（Gaussian Model）和线性模型（Linear Model）等。

通过崇州试验得到的数据，以variety表示品系处理，以output表示不同品系的各项数据，block表示区组变量，小区坐标变量为X和Y，利用这些变量及其对应的数据建立SAS数据集，空间效应模型分析的SAS程序[14]为：

Proc语句中method=REML定义方差—协方差参数估计方法为限制性极大似然法，Class语句指明试验处理因素变量为variety（品种），语句Model中编码ddfm=Satterthwaite指出自由度估计方法为Satterthwaite，Repeated语句中编码subject=intercept表示不同观测值间存在空间变异。type=sp（sph）表示空间有效应模型为球状模型。（X，Y）表示数据空间位置坐标。type后括号内的编码为空间变异模型名称的缩写，可灵活改变。可采用的空间效应模型还有指数模型（exp）、高斯模型（gau）和线性模型（1in）。常规方差分析的SAS程序可查询相关文献[13]。比较模型拟合效果时常用的拟合指标有AIC（Akaike Information Criterion）、AICC（Corrected AIC）和 BIC（Bayesian Information Criterion）等。AIC、AICC和BIC的值越小，则表明相应的模型对数据处理拟合效果越好。

2 结果与分析

2.1 对供试青贮玉米品系平均单株鲜重产量的分析数据拟合效果

由表3可知，不同供试品种的测量总株数、总鲜重和平均单株鲜重均存在很大的差异，平均单株鲜重为0.68～1.44 kg，川青8号平均单株鲜重可达1.44 kg，正大选系99/建系单株鲜重最小为0.66 kg。同一品种在不同小区间仍存在较大的差异。由表4可知，球状模型的3个信息量指标均小于方差分析模型中的信息量指标，表明试验数据之间存在一定的空间变异，采取空间模型数据分析是十分有必要的。线性模型和指数模型参数未达到收敛，因而信息指标不存在结果，这表明线性和指数模型不能描述本次试验数据空间变异。根据信息量指标越小模型拟合度越高的原则可知，空间效应球状模型对数据有更好的拟合效果。高斯模型的信息量指标大于方差分析模型，说明前者的拟合效果劣于后者。综上所述，下面用空间效应球状模型和方差分析模型进行统计分析结果的比较。

2.2 F检验和t检验

由表5可知，F检验在方差分析中和空间效应模型分析中均达到极显著水平（P＜0.05）。但概率值P=0.000 1在空间模型中小于方差分析的P=0.028 4，两种方法的第二自由度也不同。结果说明在0.05显著水平时玉米品系平均单株产量的差异在两种方法中都能检验出来。虽然两种分析方法对玉米各品系平均单株产量效应差异F检验在0.05概率水平的结论相同，但其测验效率并不相同，因为试验处理效应差异很大，即使两模型分析法F测验效率不同也都能将该差异在0.05的显著水平鉴别出来。空间效应模型的F值（F=6.17）大于方差分析模型的F值（F=2.46），说明空间效应模型分析的误差均方更小，比方差分析更灵敏，更可能发现些较小的真实差异。将所有品系与对照品种进行t检验，由表4可知，在品系间差异性检验方面，方差分析和空间效应模型分析存在着明显的差异。第一，方差分析模型标准误均相同，这是对所有品系的平均单株产量总体方差相同的假定，即主观假定区组内所有小区土壤的肥力是均匀的，但实际情况往往是区组内存在空间变异。第二，空间效应模型分析中所有两两比较的标准误均小于方差分析模型，说明空间效应模型的分析效率比方差分析模型要高，空间分析法可在一定程度上控制由于空间变异存在对试验分析结果的影响。第三，空间效应模型中所有品系比较的标准误各不相同，标准误随着所比较品种空间位置的不同而变化，反映了试验地空间变异的特征。

表3 不同供试品种收获时总株数、总鲜重产量和平均单株鲜重Table 3 Total plant number,total fresh weight yield and average fresh weight per plant were harvested for different test varieties

表4 不同模型拟合玉米品系比较试验平均单株产量数据的信息量指标值Table 4 Information index values of average yield data of single plant in the comparison test of maize fitted by different models

表5 方差分析和空间效应模型分析对玉米平均单株产量F检验的结果Table 5 Results of F test on average yield per plant of maize analyzed by variance analysis and spatial effect model

2.3 平均单株产量的估计值及排序

表6为方差分析和空间模型分析对20个品系平均单株产量的估计值及其大小排序结果。两种分析方法在平均单株产量估计值和大小排序中都存在着明显的差异。这些差异是由于两种方法对试验误差控制效果不同所造成的。按照单株平均产量的高低对品系进行筛选，从20个品系中选择出20%的优良品系，即选择4个品系。用方差分析法所选出的4个品系为8，9，17，和18，而空间效应模型选择的4个品系为1，9，10和17。空间效应模型分析中平均单株产量高的4个品系中有2个品系（1，10）被方差分析所剔除。品系1和10在方差分析中位居第5位和第9位，而在空间效应模型分析中位居第4位和第3位。这些差异说明，不同的分析方法会导致不同的品系评价。为了保障试验分析的精确度和提高品种选择的可靠性，应选用适宜的方法进行试验数据分析。

3 讨论与结论

3.1 讨论

本次试验中采用了方差分析和空间效应模型分析对青贮玉米平均单株产量进行分析。空间模型分析通过利用试验小区的空间地理位置，结合空间变异模型，有效地控制了土壤肥力差异对试验结果的影响，因此，在平均单株产量的分析中，空间模型分析具有更好的数据拟合效果和较高的分析效率，这与文献中胡希远[13，15]研究结果是一致的。研究表明[13，16]随着空间变异的增加，方差分析模型处理田间数据的误差逐渐偏大，准确性逐渐降低，相反空间模型始终保持误差较低，准确率较高。从本试验看，分析单株产量宜采用空间效应模型。不同的分析方法都存在一定的局限性，没有任一种方法对于所有指标的分析效果都是最好的，这也印证了W.W.Stroup[4]的研究。

表6 方差分析和空间效应模型分析对玉米品系平均单株产量估计值和大小排序Table 6 Estimation and ranking of average yield per plant of maize by variance analysis and spatial effect model analysis

采用空间效应模型分析，不用测定田间土壤的理化性质，以保证区组内试验条件相同或尽量相同，这样可以简化试验设计，但并不能说不需要区组试验设计，在无区组试验设计中空间模型分析效率会降低，因为空间模型在一定程度上会降低空间变异对效应值的影响，而不能完全消除，所以区组实际还是有必要的。具体过程利用SAS统计软件完成，不需进行复杂的计算。对本试验所遇到的非标准随机区组设计，空间效应模型分析同样具有适用性，所以在作物品种评比试验中，如马铃薯、小麦、油菜品种比较试验中涉及此类非标准区组设计时，建议采用空间效应模型分析，以提高分析结果的准确性。

3.2 结论

①空间效应模型分析与方差分析相比，空间效应模型分析对试验数据的拟合效果更好。

②所有品系与对照品种的两两比较t检验结果表明，空间效应模型分析的分析效率更高，对空间变异的控制能力更强。

③由于对空间变异的控制能力不同，空间效应模型分析与方差分析在F检验、t检验，品系效应估计值和大小排序结果方面都存在显著不同。