材料热工参数对混凝土箱梁横截面温度场的影响

(福州大学土木工程学院， 福建福州350116)

0 引言

温度应力是导致桥梁混凝土箱梁出现开裂的主要原因之一[1]。对于混凝土桥梁，主梁的纵向截面温度场是相近的，而主梁横截面温度场主要受材料热工参数(导热系数、比热容、质量密度、太阳辐射吸收系数、对流换热系数等)、横截面几何形状和尺寸、地理因素(桥梁方位角、地理纬度、海拔高度等)和气象条件(太阳辐射、环境温度、风速和空气混浊度等)影响[2-3]。主梁横截面温度场的影响因素多且复杂，较难依靠经典的传导方程进行精确计算，一般通过有限元法求解[4-5]。有限元法求解获得桥梁主梁横截面温度场，需要确定混凝土材料热工参数。

结构的热量传递包括三种形式：热传导、热对流以及热辐射[6]。热传导指在同个物体内不同温度的各部分之间，或者温度不同的各个物体之间，依靠物质微粒的热运动而进行的热量传递过程。影响热传导作用的热工参数主要是导热系数和比热容。导热系数指单位温差单位时间内通过单位面积的热量，反映混凝土传导热量的能力。导热系数越大表明热传导性能越好，温度达到平衡的时间就越短[7]。比热容反映的是物体在吸收或放出相同热量时的温度量。比热越大，物体升温所需要的热量越高[7]。热对流和热辐射过程涉及到的热工参数主要是对流换热系数和太阳辐射吸收系数。对流换热系数是衡量结构表面与周围环境之间的热交换量；太阳辐射吸收系数是衡量结构表面吸收太阳辐射能力的大小。由于热对流和热辐射过程的复杂性，关于对流换热系数和太阳辐射吸收系数的研究较难且较少，一般根据经验取值[6-8]。

混凝土导热系数和比热容主要受到骨料种类、骨料用量、钢筋比率和混凝土的含水状态以及外界环境温度等影响[9]。国内外学者通过试验拟合或理论模型可得到混凝土导热系数和比热容取值。有学者研究发现缺乏混凝土热工参数试验值时，可根据混凝土各组成成分的重量百分比并结合外界温度进行估算得到。还指出由估算得到的导热系数是可靠的，但比热容偏低，建议乘以1.05的修正系数[10]。王毅总结常用的混凝土热工参数取值，并考虑混凝土标号较高时，选用导热系数2.5 W/(m·℃)，比热容880 J/(kg·℃)[11]。部分学者或规范直接给出了混凝土导热系数和比热容取值[1-6,12-15]。还有部分学者采用特定的热工参数取值建立有限元模型，可较精确模拟主梁横截面温度场，但并未解释热工参数的取值原因[11,16-17]。对比国内外有关学者建议和采用的混凝土热工参数取值可以发现混凝土的热工参数取值差异较大，导热系数取值范围是0.98～3.5 W/(m·℃)，比热容取值范围是763～1200 J/(kg·℃)。

为确定混凝土热工参数对混凝土主梁横截面温度场影响，本文以一座箱梁桥为背景工程，实测其主梁横截面温度日变化。建立有限元模型，分析不同热工参数取值对主梁横截面温度日变化曲线、截面平均温度和竖向温度梯度的影响，并给出导热系数和比热容的建议取值方法。

1 热工参数对混凝土箱梁横截面温度日变化曲线影响

1.1 有限元模型建立

以深圳市马峦立交主线桥为背景工程。该桥采用等高度预应力混凝土连续箱梁结构，单幅桥面宽度17 m，梁高1.6 m，箱梁为单箱三室，上部结构主梁采用C50混凝土。全截面共布设18个温度传感器，布置方案如图1所示。其中，顶板布设5个温度传感器(T-1～T-5)；底板布设3个温度传感器(B-1～B-3)；左右腹板沿腹板从顶板中心线到底板中心线各均匀布设4个温度传感器(分别为W-1～W-4和W-7～W-10)；中腹板位置布设两个温度传感器(W-5和W-6)。

图1 温度传感器布置图Fig.1 Layout of temperature sensors

采用MIDAS-FEA根据图1的截面尺寸建立主梁横截面有限元模型。模型选用适合二维稳态及瞬态分析的2D平面应变单元，网格划分尺寸为0.02 m，模型共划分为37 017个单元，35 659个节点，如图2所示。混凝土的密度取为2 500 kg/m3[15,17]。每个节点只有温度一个自由度，每0.5 h为一个时间分析步。大气温度、风速和太阳辐射数据通过桥梁附近的小型气象站采集得到。箱外的太阳辐射、对流换热和辐射换热作用按第三类边界条件，箱内直接输入实测数据作为有限元模型边界。

图2 箱梁横截面有限元模型Fig.2 Finite element model of cross-section of box girder

1.2 导热系数影响

采用1.1节的箱梁截面有限元模型，根据导热系数取值范围是0.98～3.5 J/(kg·℃)，取1.0、1.5、2.0、2.5、3.0、3.5 W/(m·℃)六种导热系数进行分析。比热容统一取900 W/(m·℃)。导热系数和比热容主要影响热传导作用。因此夏季时，导热系数和比热容对混凝土箱梁横截面温度场的影响远大于冬季。由于篇幅限制，本文仅针对夏季温度实测时段(2017年8月10日至8月13日)开展分析。其中2017年8月13日的日温差最大、天气晴朗且太阳辐射强烈，因此本节取2017年8月13日的温度日变化曲线实测值和有限元计算值进行分析。由于篇幅限制，选取T-1、B-1、W-1和W-3测点的温度日变化曲线实测值与考虑不同导热系数的有限元计算值进行对比，如图3所示。从图3(a)可以看出，由于混凝土温度传导作用在空间和时间上的滞后性影响，在充分受到太阳照射(中午12∶00左右)之前，随导热系数增大，有限元计算的顶板T-1测点温度略微减小，但变化幅度较小可忽略。在中午12∶00之后由于受到太阳辐射作用，随导热系数增大，有限元计算的顶板T-1测点温度日变化曲线峰值增大(35.7～38.8 ℃)，变化幅度为3.1 ℃；曲线峰值的出现时间提前，变化幅度为3 h。

从图3(b)可以看出，由于基本不受太阳辐射作用影响，导热系数对有限元计算的底板温度日变化曲线的影响很小，可忽略。从图3(c)、(d)可以看出，腹板W-1测点靠近顶板，因此导热系数对其温度日变化曲线的影响规律与顶板基本一致。随导热系数增大，有限元计算的W-1测点的温度日变化曲线峰值增大(35.7～37.2 ℃)，变化幅度为1.5 ℃，影响幅度小于顶板；曲线峰值的出现时间提前，变化幅度为5 h，影响幅度大于顶板。腹板W-3测点靠近底板，因此导热系数对其温度日变化曲线的影响可忽略，与底板一致。

(a) 顶板T-1测点

(b) 底板B-1测点

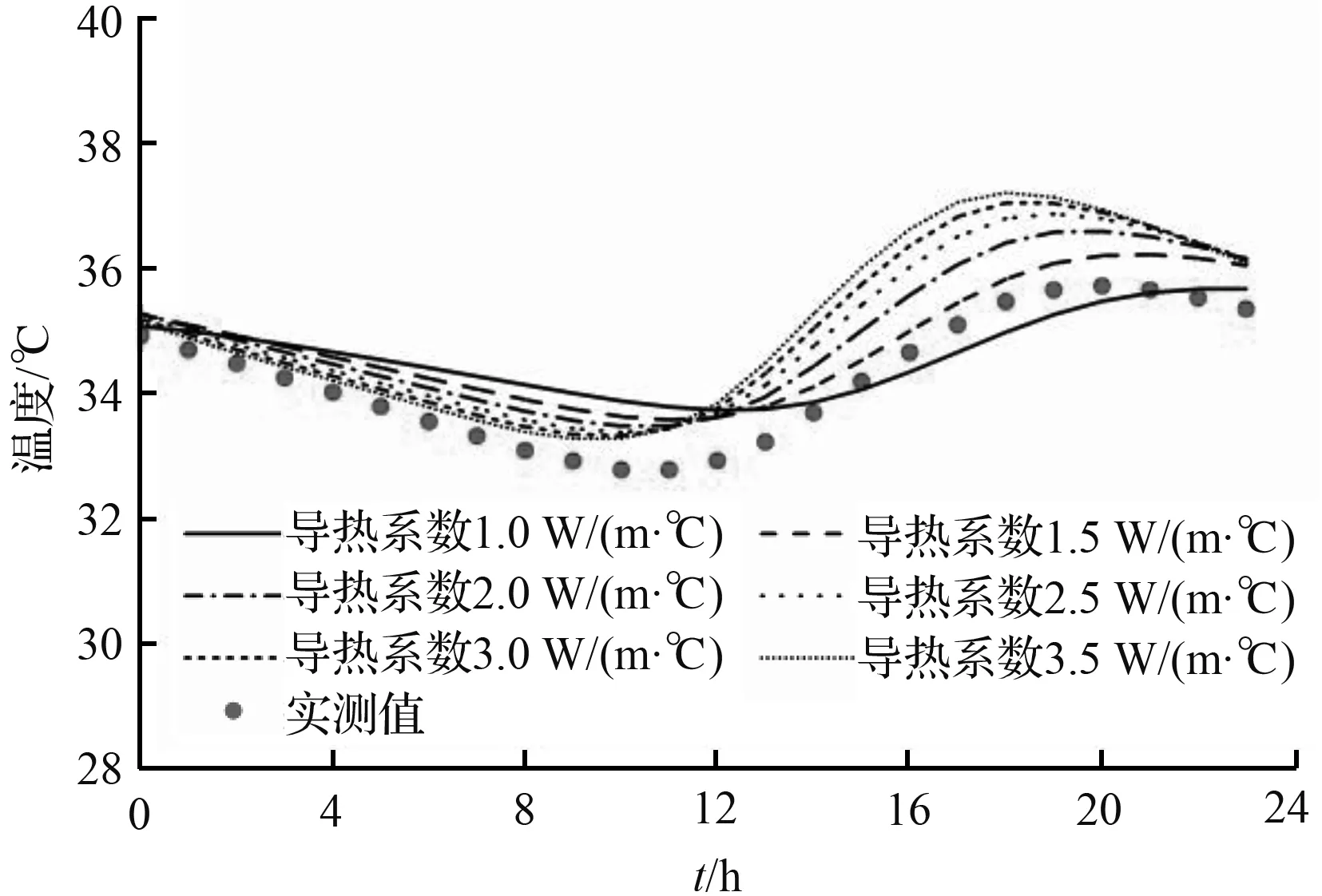
(c) 腹板W-1测点

(d) 腹板W-3测点

图3 不同导热系数对箱梁横截面测点温度日变化曲线影响
Fig.3 Influence of different thermal conductivities on hourly temperature curves of box girder

为评价温度日变化曲线实测值与考虑不同导热系数的有限元计算值的拟合程度，本文采用均方根误差(ERMS)[公式(1)]和平均相对误差(EMAP)[公式(2)][18]。

(1)

(2)

式中：yi,c指计算值，yi,m指实测值。

温度日变化曲线实测值与不同导热系数有限元模型计算值的ERMS和EMAP值对比于表1。分析发现，当导热系数取值范围是1.0～3.5 W/(m·℃)时，底板B-1测点和腹板W-3测点的ERMS最大差值为0.30 ℃(变化范围0.19～0.49 ℃)，EMAP最大差值为0.99 %(变化范围0.53 %～1.52 %)。导热系数取1.5 W/(m·℃)时，顶板T-1测点和腹板W-1测点的温度日变化曲线实测值与有限元计算值吻合最佳。当导热系数从1.0 W/(m·℃)变化到2.0 W/(m·℃)时，顶板T-1测点和腹板W-1测点的ERMS最大差值仅为0.19 ℃，EMAP最大差值仅为0.61 %。因此可以判断当导热系数介于1.0～2.0 W/(m·℃)时，混凝土箱梁横截面的温度日变化曲线实测值与有限元计算值均吻合较好。

表1 温度日变化曲线实测值与不同导热系数有限元模型计算值对比
Tab.1 Comparison of hourly temperature curves obtained by field monitoring andfrom the finite element models with different thermal conductivities

导热系数/(W·m-1·℃-1)顶板T-1底板B-1腹板W-1腹板W-3ERMS/℃EMAP/%ERMS/℃EMAP/%ERMS/℃EMAP/%ERMS/℃EMAP/%1.00.772.150.481.450.631.600.200.541.50.742.090.47 1.450.591.660.190.532.00.932.700.47 1.440.711.990.240.642.51.143.170.481.430.842.200.310.913.01.333.540.481.420.962.340.401.233.51.493.840.491.411.052.430.491.52

1.3 比热容影响

采用1.1节的箱梁截面有限元模型，根据比热容取值范围是763～1 200 J/(kg·℃)，取700、800、900、1 000、1 100、1 200 J/(kg·℃)六种比热容进行分析。由1.2节分析可知导热系数取1.5 W/(m·℃)时，混凝土箱梁横截面的温度日变化曲线实测值与有限元计算值吻合程度最佳，因此本节有限元模型的导热系数取1.5 W/(m·℃)。由于篇幅限制，选取T-1、B-1、W-1和W-3四个测点的温度日变化曲线实测值与考虑不同比热容的有限元计算值进行对比，如图4所示。从图4(a)可以看出，随比热容增大，在充分受到太阳照射(中午12∶00左右)之前，有限元计算的顶板T-1测点温度增大；中午12∶00之后，有限元计算的顶板T-1测点温度日变化曲线峰值减小(37.6～35.9 ℃)，变化幅度为1.7 ℃；曲线峰值的出现时间延迟，变化幅度为1 h。

(a) 顶板T-1测点

(b) 底板B-1测点

(c) 腹板W-1测点

(d) 腹板W-3测点

图4 不同比热容对箱梁横截面测点温度日变化曲线影响
Fig.4 Influence of different specific heat capacities on hourly temperature curves of box girder

从图4(b)可以看出，由于基本不受太阳辐射作用的影响，比热容对有限元计算的底板温度日变化曲线的影响很小，可忽略。从图4(c)、(d)可以看出，腹板W-1测点靠近顶板，因此比热容对其温度日变化曲线的影响规律与顶板基本一致。随比热容增大，有限元计算的W-1测点的温度日变化曲线峰值减小(35.7～36.8 ℃)，变化幅度为1.1 ℃，影响幅度小于顶板；曲线峰值的出现时间延迟，变化幅度为3 h，影响幅度大于顶板。腹板W-3测点靠近底板，因此比热容对其温度日变化曲线的影响可忽略，与底板一致。比热容对混凝土箱梁横截面温度日变化曲线的影响小于导热系数。

温度日变化曲线实测值与不同比热容有限元模型计算值的ERMS和EMAP值对比于表2。分析发现，当比热容取值范围是700～1200 J/(kg·℃)时，底板B-1测点和腹板W-3测点的ERMS最大差值为0.11 ℃(变化范围0.43～0.54 ℃)，EMAP最大差值为0.37 %(变化范围1.26 %～1.63 %)。当比热容取值范围是800～1 000 J/(kg·℃)时，顶板T-1测点和腹板W-1测点的ERMS最大差值仅为0.19 ℃，EMAP最大差值仅为0.54 %。因此可以判断当比热容介于800～1 000 J/(kg·℃)时，混凝土箱梁横截面的温度日变化曲线实测值与有限元计算值均吻合较好。

表2 温度日变化曲线实测值与不同比热容有限元模型计算值对比Tab.2 Comparison of hourly temperature curves obtained by field monitoring and from the finite element models with different specific heat capacities

2 热工参数对混凝土箱梁横截面平均温度影响

我国公路桥规(JTG D60—2015)考虑的温度作用主要包括桥梁结构均匀温度作用和竖向温度梯度两个部分[19]。基于1.1节的有限元模型，分析不同热工参数取值对箱梁横截面平均温度的影响。有限元模型每个节点只有温度一个自由度，且每个节点所覆盖的面积相同。因此，将每个时刻的节点温度总和除以节点总数，可得到每个时刻的主梁截面平均温度[20]。2017年8月13日的混凝土箱梁横截面平均温度曲线最大值的实测值与考虑不同热工参数的有限元计算值，汇总于表3。分析表3数据可以发现，随导热系数增大或比热容减小，混凝土箱梁横截面平均温度曲线最大值略微增大，变化幅度仅为0.9 ℃。因此，热工参数对混凝土箱梁横截面平均温度曲线最大值的影响可忽略。

表3 不同热工参数对箱梁横截面平均温度的影响Tab.3 Influence of different thermal parameters on the average temperature of box girder

3 热工参数对混凝土箱梁横截面竖向温度梯度影响

箱梁横截面竖向温度梯度指的是沿横截面高度方向的温差变化曲线。在竖向温度梯度作用下，混凝土箱梁在自身内部温度的非线性分布下产生不均匀变形和外部多余约束下引起相应的温度内约束应力和温度外约束应力，也称为温度自应力和温度次应力。本节基于1.1节的有限元模型，分析不同热工参数取值对箱梁横截面竖向温度梯度的影响。分析图3发现，2017年8月13日的箱梁横截面最大竖向正温差发生于15：00。考虑不同热工参数的混凝土箱梁横截面最大竖向正温度梯度曲线的有限元计算值如图5所示。图中竖坐标为距顶板上缘的距离，0～45 cm属于顶板，45～118 cm属于腹板，118～160 cm属于底板。考虑不同热工参数的顶板、腹板和底板的最大竖向正温差对比列于表4。

从图5(a)和表4可以看出，不同导热系数对混凝土箱梁横截面竖向温度梯度曲线影响较大。在顶板范围内，距顶板上缘8 cm范围内，随导热系数增大，顶板正温差减小(17.0～13.1 ℃)。顶板上缘表面处的正温差减小幅度最大，减小幅度分别为0.9、1.8、2.6、3.3、3.9 ℃。距顶板上缘8～45 cm范围内，随导热系数增大，顶板正温差增大，增大幅度最大值为1.9 ℃。在腹板范围内，随导热系数增大，腹板正温差减小，减小幅度最大值为0.6 ℃。在底板范围内，距顶板上缘118～156 cm范围内，随导热系数增大，底板正温差增大，增大幅度最大值为0.5 ℃；距顶板上缘156～160 cm范围内，随导热系数增大，底板正温差减小。底板下缘表面处的正温差减小幅度最大，减小幅度最大值为1.1 ℃。

从图5(b)和表4可以看出，不同比热容对混凝土箱梁横截面竖向温度梯度曲线影响较大。在顶板范围内，随比热容增大，顶板正温差减小。距顶板上缘8 cm处的正温差减小幅度最大，减小幅度最大值为2.5 ℃。在腹板范围内，不同比热容对腹板正温差影响仅为0.2 ℃，可忽略不计。在底板范围内，随比热容增大，底板正温差减小，减小幅度最大值为0.8 ℃。比热容对混凝土箱梁横截面竖向温度梯度曲线的影响小于导热系数。

(a) 不同导热系数

(b) 不同比热容

表4 不同热工参数对箱梁横截面最大竖向正温差的影响Tab.4 Influence of different thermal parameters on the maximum positive vertical temperature differences of box girder

4 结论

为确定混凝土热工参数对混凝土箱梁横截面温度场影响，本文通过温度实测、有限元模拟和参数分析，主要得到以下结论：

① 受到太阳照射之后，随导热系数增大或比热容减小，顶板和腹板上部的温度日变化曲线峰值增大，变化幅度最大值为3.1 ℃；曲线峰值的出现时间提前。导热系数和比热容对腹板下部和底板温度日变化曲线的影响可忽略。比热容对混凝土箱梁横截面温度日变化曲线的影响小于导热系数。

② 当导热系数介于1.0～2.0 W/(m·℃)，比热容介于800～1000 J/(kg·℃)时，混凝土箱梁横截面的温度日变化曲线实测值与有限元计算值均吻合较好。

③ 随导热系数增大或比热容减小，混凝土箱梁横截面平均温度曲线最大值略微增大，变化幅度仅为0.9 ℃。热工参数对混凝土箱梁横截面平均温度曲线最大值的影响可忽略。

④ 不同热工参数对混凝土箱梁横截面竖向温度梯度曲线影响较大。在顶板范围内，随导热系数或比热容增大，顶板正温差减小，减小幅度最大为3.9 ℃。在腹板范围内，不同热工参数对腹板正温差影响很小，可忽略不计。在底板范围内，随导热系数或比热容增大，底板正温差减小，减小幅度最大值为1.1 ℃。比热容对混凝土箱梁横截面竖向温度梯度曲线的影响小于导热系数。