中国股债市场长期动态相关性的影响因素研究
李乐天 厉璇 胡瑞临 李滨

摘 要:本文借鉴现代宏观经济学中的无套利仿射模型,基于“定价核”的定价方式,将股票市场和债券市场收益率之间的相关系数分解为其主要驱动因素——通货膨胀、真实利率和股息率的不确定性,以及三者之间的协方差。在实证部分,采用DCC-MGARCH模型计算股票市场和债券市场收益率的动态相关系数,验证中国股债相关性的时变规则;进而通过回归分析探究所选取的解释变量对中国股债相关性的贡献。结果表明,通货膨胀和股息率的不确定性以及真实利率与通货膨胀和股息率各自之间的协动性是影响这种相关性的主要因素;通胀冲击、真实利率和股息率可以解释这种相关性与长期动态的暂时背离。其中,通货膨胀和股息率的不确定性对股债相关性的影响与其他欧美主要经济体有着不同的表现,反映了中国市场的特殊性;此外,相较于中国经济市场的平稳时期,股市动荡期间各经济因素的影响会发生改变,且模型解释力会降低。
关键词:动态相关系数;无套利仿射模型;定价核;DCC-MGARCH
一、引言与文献综述
依据现代投资组合理论,不同资产的收益率、波动率及其两两之间的相关性对于资产配置至关重要(Markowitz,1952)[1]。为实现风险分散,投资者通常倾向于投资相关性较弱的不同类资产,以实现风险的分散化。当一个投资组合仅包含股票和债券时,股票和债券收益率之间的相关性就成为组合配置的一个关键变量。当两资产收益间的相关系数相对其长期水平发生偏离时,利用现代投资组合理论进行资产组合配置将会因配置方向有误而造成损失。因此对于机构投资者和对技术要求较高的个人投资者而言,预判股票和债券的共同变动趋势,有助于他们分散风险,及时调整持仓以及进行重新配置。研究股票和债券市场的相关关系及其影响因素,对于金融监管来说也同样具有重要的现实意义。
随着我国资本市场的发展,对于有效资产配置进行研究的需求持续增加。查阅文献可知,根据国外的研究结果,股债的收益率相关性随着时间会发生大幅波动,并且在正、负值之间频繁跳动(Gulko,2002;Ilmanen,2003;Campbell等,2009;Perego和Vermeulen,2016)[2,3,4,5]。Boyd等(2005)[6]、Yang等(2009)[7]认为股债市相关性会受到通货膨胀水平、经济发展阶段、利率等月度宏观指标的影响。在市场不确定性方面,DAddona和Kind(2006)[8]使用月度数据,发现股债相关性与实际利率的波动水平呈正相关,与通货膨胀率的波动水平呈负相关。Asgharian等(2016)[9]引入宏观金融因素,发现当经济疲软时,相关性往往较小且呈负相关,支持了“安全投资转移”现象。国内研究方面,袁超等(2008)[10]认为由于经济运行情况和宏观政策等外部的不确定性因素的影响,股债两市的相关性为结构性变化,两个市场对冲击的反应程度并不相同。钱智俊和李勇(2017)[11]认为基准利率、经济增速和自相关性是中国股债收益相关系数条件均值的主要影响因素。
近年来,我国股债收益相关性的时变特征和时变原因逐步成为国内研究的热点。曾志坚和江州(2007)[12] 通過计算我国股债收益率的月度 Pearson 相关系数发现该相关系数长期在[±]0.3之间波动,并存在着时变性特征。陈志英和郑振龙 (2011)[13]的研究显示,股债相关性是时变的,股票市场的不确定性和预期通货膨胀率是影响股债相关性的主要因素。针对股债收益相关性的时变现象,国外研究(Connolly 等,2005;Aslanidis和Christiansen,2014)[14,15]多采用高频数据测算股债市场的相关系数,并提出了诸多理论解释。由于国内证券市场起步较晚,反映宏观基本面和市场不确定性的指标只能得到相对低频的月度数据。又由于样本容量少、数据频率不一致等问题,一些国内文献仅定性地解释货币供给量、经济发展阶段等宏观基本面因素如何作用于两市场的共同运动(Li和Zou,2008;袁超等,2008;肖利平,2011)[16,10,17]。另一些定量分析的文献则将频率较高的日或周数据转化为低频的月度数据,进而分析宏观因素对股债市相关性的影响(王茵田和文志瑛,2010)[18]。
本文分析了2006—2018年中国股票和债券市场收益率的相关性。由于之前的研究成果大多基于确定性宏观因素,故当市场发生意外波动时,无法有效地对股债市场的相关系数进行测算。本文基于已有研究成果,边际贡献如下:
第一,从不确定性角度入手,使得应对意外波动情况时,结论具有更强的说服力和可实践性。为得到不确定性度量,本文借鉴无套利仿射模型和“定价核”理论,对债券和股票进行定价,该模型通过推导股票和债券的真实收益率,在计算条件协方差时将不确定性渠道与确定性渠道分离,从而给出不确定性的公式化表述。
第二,在实证部分,本文通过回归变量上的股债相关性来实证检验这种分解:(1)对于中国股票与债券市场收益的动态相关系数的计算,选用DCC-MGARCH模型,其优势如下:DCC-MGARCH模型的条件均值方程刻画了收益率的序列自相关性,其条件方差方程刻画了收益率的“波动聚类”特征。因此,相较Pearson相关系数等其他指标更为有利之处在于,该模型得到的条件相关系数排除了中国市场高频数据缺失的干扰。而且,DCC-MGARCH模型是动态模型,能更好地展示不同资产收益的条件相关系数的时变性,并得到一条完整的波动路径。(2)根据中国金融市场重大事件将观测区间分割。这样不仅可以排除金融市场压力区间(如2008年次贷危机与2015年股市异常波动等)所带来的估计偏差,使回归方程的估计结果更加准确,也可进一步研究各经济因素在不同时期对股债市场相关性的贡献。
二、模型研究
股票和债券的价格从本质上来说是它们预期未来现金流的贴现。假设没有违约风险,股票的现金流是不确定股利的无限流,而债券的现金流是预先确定的票面收益的固定支付数量。显然,共同影响两者贴现的因素可能会使股票和债券的价格向同一方向变化,而只影响股票股息的因素则会降低它们的协动性,即协方差。Li等(2003) [19]针对真实利率、通货膨胀和股息率建立宏观的无套利仿射模型,基于定价核探究股票和债券收益率的相关性,其具有较强的经济学解释,并且结果更加直观。本文聚焦上述见解,借鉴其模型和方法,通过内生推导探究股票和债券的收益以及它们的相关性:
(一)债券和股票的定价
资产真实价格的定价核[Mt]可以定义为一个正随机过程,假设一种资产在[t]时刻的价格为[Pt],则有:
定价核[Mt]在无套利假设下的存在性和唯一性条件已由Harrison等(1979)[20]得到,而Bekaert等(2001)[21]提出了一种刻画定价核的方法,具体形式为:
接着,本文采用Pericoli(2018)[22]的方法来研究债券和股票的定价和收益率:定义资产价格方程,利用定价核建立资产的期限递归公式,最后通过待定系数的方法进行求解,并在资产价格的基础上,求出对数收益率。
1. 债券收益率。无违约风险的债券价格是现金流名义贴现的总和,因此,它的公允價值由定义名义贴现率所需的所有变量决定:即真实利率和通货膨胀。考虑一个在n个周期支付1元的名义零息债券,从t期到t +1期的收益率是真实利率、期限溢价、预期通胀加上通货膨胀和真实利率冲击之和,具体为:
式(9)的前三项表示预期债券收益率为真实利率、预期通货膨胀率和期限溢价之和;后两项表明来自真实利率和非预期通货膨胀的波动对债券的价格也有一定影响。真实利率、预期通货膨胀和期限溢价的增长都会引起债券收益率的增长,这一点符合实际;一般情况下,假设真实利率和通货膨胀的随机过程是平稳的,即[|αr|<1],[0<απ<1],因此有[Arn-1<0],[Aπn-1<0],这意味着非预期通货膨胀和真实利率的正向波动可能导致债券收益率下降;[An-1r]和[An-1π]的绝对值随n递增,即期限越长的债券越容易受到来自两者波动的影响,且期限溢价会越来越低。
2. 股票收益率。由于股票可以带来实际股息,因此股票的定价不需要像债券定价那样调用名义定价内核,其价格主要由真实利率和股息率决定。考虑一个遵循股息收益率过程δt的股票,其对数收益率可以表示成真实利率、风险溢价、预期通胀加上通货膨胀、股息率和真实利率冲击之和,具体为:
式(10)的前三项表示预期股票收益率。预期股票收益率和预期债券收益率具有两个相同的组成部分:真实利率和预期通货膨胀率;后两项表明股票收益率不仅受到真实利率和非预期通货膨胀波动的影响,还受到股息收益率波动的影响。一般情况下,[ar<0],[aδ>0],这意味着通货膨胀的非预期正向波动可能导致股票收益率下降,股息收益率的正向波动可能导致股票收益率的增长。
由式(9)(10)可以看出,预期通货膨胀、真实利率及其波动是股票和债券相同方向变化的共同驱动因素,而受股息波动的影响是股票独有的。这一结果与Fama等[23]的实证结果一致,即债券的定价因素只是股票定价因素的一个子集。
(二)股票和债券的相关系数
上式的第一部分表明,由于[Arn-1ar>0],真实利率不确定性的增加可能增强股票和债券收益率的协动性。因为真实利率决定了现金流的贴现,又同时决定着股票和债券的价格。
第二部分说明了非预期通货膨胀通过名义渠道、现金流渠道和贴现因子渠道影响股票和债券的协动性。由于[Aπn-1<0],非预期通货膨胀通过名义渠道可能会削弱股票和债券的协动性:股票收益可以对冲通货膨胀的增长,而通胀增长却会减少债券收益,因此投资者会更加青睐股票,从而降低股债相关性。另外两个渠道产生的影响不确定并可能具有时变性,依赖于参数([ρδπ],[ρπr]和[[Aπn-1ar+Arn-1]])。
第三部分表明,股息率和真实利率的协方差构成了投资组合再平衡渠道。一般来说,这一项与股债收益率相关性的实际表现相近,因此对其贡献相对较大,但驱动方向不能确定,且一样可能具有时变性。
综上所述,该模型将三个宏观经济因素的不确定性及其之间的相互联系作为股票和债券相关性的解释因素:预期通货膨胀和真实利率的不确定性增强了这种相关性;而非预期通货膨胀的影响是不确定的,取决于股息率和真实利率是否受到非预期通货膨胀波动的影响。此外,股息率的不确定性也会单方面改变股票收益率,从而降低股票和债券收益率的相关性。
值得注意的是,股票和债券收益率的相关性和协方差有所不同,后者还与股票和债券收益率的方差有关,所以决定股债收益率相关性的因素及其影响方式与式(11)有所出入。
下文将基于上述影响股票和债券收益率相关性的因素进行回归分析,进一步探究中国股票市场和债券市场收益率相关性的决定因素。
三、指标构建和数据说明
本文分别选取按流通市值加权的深沪两市A股综合收益率和中债综合全价指数收益率代表股票市场的收益率和债券市场的收益率。
深沪两市A股综合收益率衡量了两个市场 A 股的收益率,比上证综合指数更具代表性[13]。同时,中债综合全价指数收益率的债券范围更加全面,且其时间序列更加完整。
股票市场和债券市场收益率的样本区间从2006年10月到2018年12月,共147个月观测值,相关数据均收自万得金融数据库。
由于我国股债数据时间区间的限制,本文采用DCC-MGARCH模型计算股票和债券收益率的相关系数,该模型很好地刻画了条件相关系数的时变特征[24],较直接计算Pearson相关系数来说更加准确。根据我国市场情况,假设股票和债券的收益率均服从AR(1)过程,波动率方程设定为GARCH(1,1)形式。具体方程如下:
(1)通货膨胀的不确定性(Vol_INF)、真实利率的不确定性(Vol_REL)和股息率的不确定性(Vol_DID)均以通过EGARCH(1,1)模型所拟合波动值作为两者不确定性的测量[25,26],假设通货膨胀率和真实利率均服从AR(1)过程。通货膨胀率和真实利率的测度也极为关键。查阅资料可知,我国的通货膨胀率主要通过CPI(消费物价指数)进行度量。本文选取上月为100的CPI指数,具体计算公式为:
此外,本文还引入一些其他变量作为影响股票和债券收益率相关性的解释因素:
(1)宏观市场流动性(EM2G)。采用M2/GDP表示货币流动性,取其对数差分表示宏观市场流动性。货币政策显然会对股票市场和债券市场产生一些影响,其中最重要的是货币流动性[13]。货币流动性反映货币在市场上的投放量,其变化会引起股票和债券的需求,而两者受到影响的程度往往不同,从而导致股市和债市收益率的相关性变化。M2的数据来自万得金融数据库。
(2)经济周期(CYCLE)。基于采购经理指数PMI的对数差分来代表经济周期。在经济周期的不同阶段,股票市场和债券市场的表现也是不同的。一般情况下,在经济扩张阶段投资者更加青睐股票的高收益;在经济緊缩阶段,投资者理应重视长期债券[27]。采购经理指数PMI是一套综合性的经济监测指标体系,能够反映经济的整体增长和衰退,因此如下定义衡量经济周期的指标:
四、实证分析
(一)股票和债券收益率相关系数的变化特征
深沪两市A股综合收益率和中债综合全价指数收益率的变化如图1所示,其描述性统计特征如表2所示。
DCC-MGARCH模型要求序列平稳且有异方差性、自相关性。故对股票市场和债券市场收益率进行ADF单位根检验、ARCG效应检验和Ljung-Box检验:ADF检验中两者均包含常数项且不含趋势项,滞后阶数为3,结果充分表明股债市场收益率序列是平稳的;ARCH效应检验中两者滞后阶为5,结果显示股债市场收益率存在明显的异方差;Ljung-Box检验取滞后阶数为20,结果显示股债市场收益率具有显著的自相关性。上述检验均说明采用DCC-MGARCH模型是合理的。
基于上述信息的支撑,采用DCC-MGARCH模型计算股票市场和债券市场收益率的动态相关系数,假设股票和债券的收益率均服从AR(1)过程,波动率方程设定为GARCH(1,1)形式。
系数估计的结果如表3所示。结果表明,AR(1)方程的[β1]和[β2]都在10%以上的置信水平下显著,说明我国股票市场和债券市场的收益率均有很强的自相关。GARCH(1,1)方程的[δ1]、[δ2]、[η1]和[η2]的估计显著为正,充分表明了股票市场和债券市场收益率的ARCH效应。DCC-MGARCH(1,1)方程的k和λ也在1%的置信水平下显著,直接地表明了中国股债市场相关性的时变性。这些结论都与上文的ARCH效应检验和Ljung-Box检验相对应。
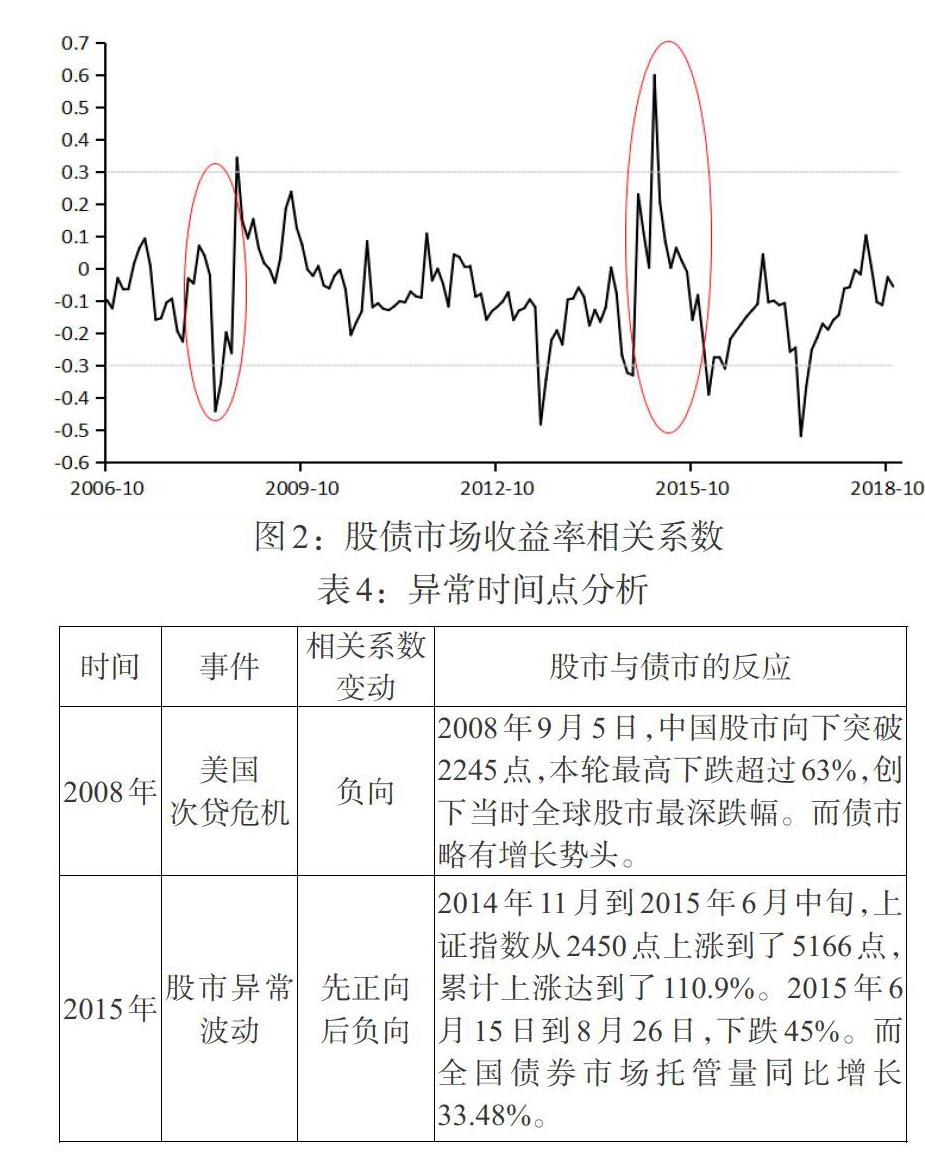
2006年10月到2018年12月中国股债市场的动态相关系数如图2所示。可以看出,股债市场收益率的相关系数变化非常复杂,间断性出现正相关或者负相关,波动幅度较大,但大部分时间表现为正相关。
根据曾志坚和江州(2007)[12]的计算,我国股债收益率相关系数长期在-0.3—0.3之间波动。而由本文结果可以看出,在观测区间内多个尖峰点偏离了这个区间。本文选取两个典型的异常点进行分析,见表4。
2007年,美国发生了次贷危机,引发全球金融危机。随着国际金融市场的风险传导效应增强,我国股市受到了一定影响。而债市的投资主体普遍而言是机构投资者,其风险偏好较低,对经济基本面的捕捉和反应也较全面,故债市呈现稳定增长的趋势。
2015年,由于对经济转型发展的预期过高,市场存在大量短期套利继而逃离的投机者,“高杠杆配置”成为2015年股市震荡的直接“导火索”,另外,监管不到位、滞后的因素不容忽视。而同时债券市场增量和规模快速扩大,全年发行规模达22.3万亿元,同比增长87.5%。债券市场对内放松管制与对外开放并行,机制与产品创新不断,市场基础设施间差异化竞争有序进行,形成改善服务、提高市场效率的良性发展格局。
(二)回归分析及结果
采用多种检验方法对所有相关变量进行性质检验,结果如表5所示。其中,ADF检验的滞后阶由SIC准则决定,rt、δt、EM2G、CYCLE包含趋势项和常数项,其他均只包含常数项;ARCH效应检验滞后阶为5;Ljung-Box检验取滞后阶数为20。结果表明,πt,rt,δt均适用于(E)GARCH模型,这说明了本文解释变量设计的合理性。
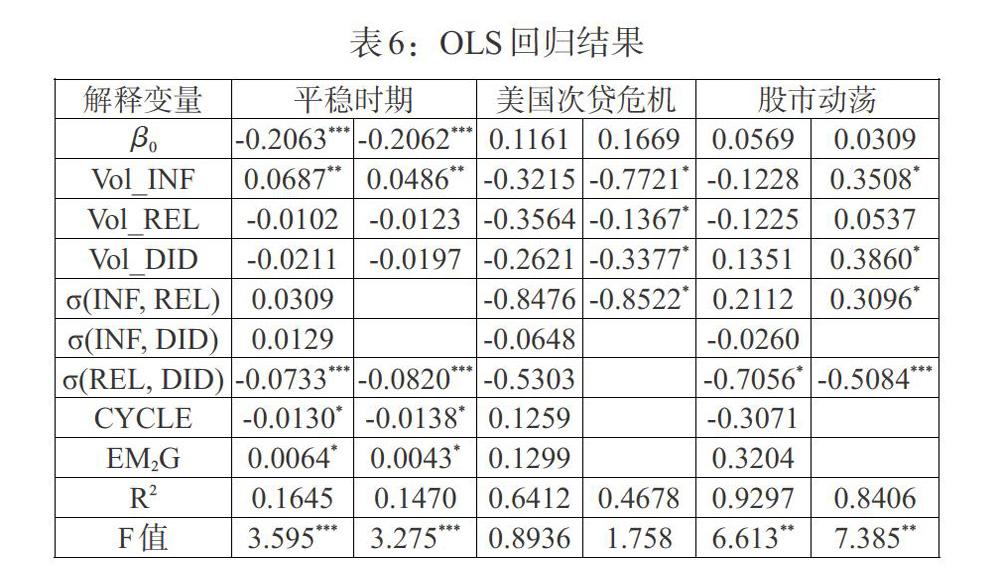
根据上述对中国股债市场收益率相关性异常波动的分析,将观测区间分为三段:美国次贷危机期间(2008年4月到2009年4月),股市异常波动期间(2014年10月到2015年10月),以及股债市平稳发展期间(2006年10月到2018年12月内的其他时间)。这样不仅可以消除在分析股债收益率相关性的影响因子时异常波动所带来的偏差,也可以更深一步地研究特殊事件引发的股债相关性影响因子的变化。分割观测区间,并将解释变量依次加入OLS回归模型中,结果如表6。
由回归结果分析可得,在平稳时期部分回归系数的显著性和总体方程的显著性均较高,可以认为宏观市场的不确定性以及各因子之间的协动性对中国股债收益率的相关性有着显著的影响:
(1)通货膨胀的不确定性是股债相关性的正向驱动;而真实利率和股息率的不确定性是股债相关性的负向驱动,但它们的影响并不显著。
(2)通货膨胀、真实利率和股息率之间的协动性也在一定程度上影响股债相关性:通货膨胀和真实利率、通货膨胀和股息率的协动性与股债相关性呈正相关,而股息率和真实利率的协动性与股债相关性呈显著的负相关。
(3)经济周期和宏观市场流动性对股债相关性也均有着显著影响:经济的扩张阶段,股票和债券的收益率往往呈现一种负相关;而经济衰退时,股票和债券的收益率则同向波动;宏观市场流动性推动了股债市场的正相关。
在金融市场压力区间,市场风险增大,股债收益率的相关性趋向极端,决定其变化的因素也更加难以确定。美国次贷危机和中国股市异常波动期间,决定中国股债相关性的因子均有一定程度的变化,甚至解释性大幅降低:
(1)美国次贷危机期间,通货膨胀、真实利率、股息率的不确定性均成为股债相关性显著的负向驱动;通货膨胀和真实利率的协动性对股债相关性的负向影响增强,而真实利率和股息率协动性的影响几乎消失;经济周期和宏观市场的流动性也不再是决定股债相关性的因素。
(2)美国次贷危机期间,由于中国股市遭受巨大影响,波动幅度增加,股债相关性一度减弱。从回归分析的结果可以看出,总体方程的显著性较低,由此运用普遍模型预测股债收益率的相关性变得十分困难,需要更进一步探究更具有适应性的因素。
(3)2015年股市异常波动期间,回归系数的符号和显著性变化较大,但是总体方程依然是显著的,故可以认为:通货膨胀、真实利率、股息率的不确定性均成为股债相关性的正向驱动;相较于平稳时期,通货膨胀和真实利率协动性的正向贡献更为显著,真实利率和股息率协动性的负向影响力也更强;经济周期和宏观市场的流动性对股债相关性的决定甚微。
从上述结果分析来看,决定股债收益率相关性的因素反映了我国金融市场的一些特殊性:许多研究发现,在大部分欧美国家,通货膨胀的不确定性往往是股债收益率相关性的负向驱动[22],而我国则相反,这是由于我国长期有着较欧美更高的通货膨胀率,导致非预期通货膨胀也处于高位[25],因此股票收益所带来的对冲效果被削弱,投资者更加青睐于分散投资。另外,我国长期存在企业分红少甚至不分红的现象,所以股息率总维持在一个较低且不稳定的水平,所以股息率的不确定性对股债相关性的影响并不显著。
五、结论
本文结合我国股债市场的情况,建立三大主要经济指标(真实利率、通货膨胀率、股息率)的仿射模型,基于定价核内生推导出影响股债市场相关性的决定因素,分析了在宏观不确定性和协动性的角度下我國股债市场收益率相关性的影响机理。本文的研究得出以下结论:
第一,2006年10月至2018年12月这一期间内,我国股债市场的收益率相关性存在时变性,且间断性出现正相关或负相关,股债收益率波动幅度较大说明我国资产管理行业面临着股债相关性突变的风险。
第二,平稳时期股债市场相关性主要由通货膨胀的不确定性正向驱动。故当通货膨胀更加不稳定时,通过资产组合、分散投资来降低风险会因资产间相关系数的增大而受损。而经济动荡时期,影响我国股债市场相关性的因素则更为多变和复杂,需要结合不同经济事件背景独立分析。
第三,在平稳时期,通货膨胀、真实利率和股息率之间的协动性也在一定程度上影响股债相关性:股息率和真实利率的协动性与股债相关性呈显著的负相关。而经济动荡时期,则需要针对不同事件更进一步探究更具有适应性的影响因素。
第四,平稳时期经济周期和宏观市场流动性对股债相关性均有着显著影响:经济的扩张阶段,股票和债券的收益率往往呈现一种负相关,而经济衰退时,股票和债券的收益率一般会同向波动;宏观市场流动性则正向推动了股债市场的相关。在经济动荡时期,经济周期和宏观市场的流动性对股债相关性的决定甚微。
参考文献:
[1]Markowitz,H.M. 1952. Portfolio Selection [J].Journal of Finance,7(1).
[2]Gulko,Les. 2002. Decoupling [J].The Journal of Portfolio Management,28(3).
[3]Ilmanen A. 2003. Stock-bond Correlations [J].The Journal of Fixed Income,13 (2).
[4]Campbell J Y,Sunderam A,Viceira L M. 2009. Inflation Bets or Deflation Hedges? The Changing Risks of Nominal Bonds [J].Social Science Electronic Publishing,(14701).
[5]Perego E R,Vermeulen W N. 2016. Macro-economic Determinants of European Stock and Government Bond Correlations:A Tale of Two Regions [J].Journal of Empirical Finance,37.
[6]Boyd J H,Jian H U,Jagannathan R. 2005. The Stock Market\"s Reaction to Unemployment News: Why Bad News Is Usually Good for Stocks [J].The Journal of Finance,60(2).
[7]Yang J,Zhou Y,Wang Z. 2009. The Stock-bond Correlation and Macroeconomic Conditions: One and A Half Centuries of Evidence [J].Journal of Banking & Finance,33(4).
[8]D'Addona S,Kind A H. 2006. International Stock-Bond Correlations in a Simple Affine Asset Pricing Model[J]. SSRN Electronic Journal,30(10).
[9]Asgharian H,Christiansen C,Hou A J. 2016. Macro-Finance Determinants of the Long-Run Stock-Bond Correlation:The DCC-MIDAS Specification [J].CREATES Research Papers,14(3).
[10]袁超,张兵,汪慧建. 债券市场与股票市场的动态相关性研究 [J].金融研究,2008,(1).
[11]钱智俊,李勇.宏观因子、投资者行为与中国股债收益相关性——基于动态条件相关系数的实证研究 [J].国际金融研究,2017,367(11).
[12]曾志坚,江洲.关于我国股票市场与债券市场收益率联动性的实证研究 [J].当代财经,2007,(9).
[13]郑振龙,陈志英.中国股票市场和债券市场收益率动态相关性分析 [J].当代财经,2011,(2).
[14]Connolly R,Stivers C,Sun L. 2005. Stock Market Uncertainty and the Stock-bond Return Relation [J].Journal of Financial and Quantitative Analysis,40 (1).
[15]Aslanidis N,Christiansen C . 2014. Quantiles of the realized stock-bond correlation and links to the macroeconomy [J].Journal of Empirical Finance,(28).
[16]Li X,Zou L. 2008. How Do Policy and Information Shocks Impact Co-Movements of Chinas T-Bond and Stock Markets? [J].Journal of Banking & Finance,32(3).
[17]肖利平.中國债券市场与股票市场间波动溢出效应——基于SJC—Copula模型的分析 [J].证券市场导报,2011,(9).
[18]王茵田,文志瑛.股票市场和债券市场的流动性溢出效应研究 [J].金融研究,2010,(3).
[19]Li L. 2003. Macroeconomic Factors and the Correlation of Stock and Bond Returns [J].Social Science Electronic Publishing.
[20]Harrison J,Kreps D M. 1979. Martingales and Arbitrage in Multiperiod Securities Markets [J].Journal of Economic Theory,20(3).
[21]Bekaert G,Grenadier S R. 2001. Stock and Bond Pricing in an Affine Economy [J].Social Science Electronic Publishing.
[22]Pericoli M. 2018. Macroeconomics Determinants of the Correlation between Stocks and Bonds. Temi di discussione(Economic working papers).
[23]Fama E F,French K R. 1993. Common Risk Factors in the Returns on Stocks and Bonds [J].Journal of Financial Economics,33(1).
[24]郑良海,侯英.银行间债券市场和交易所债券市场动态关系研究——基于DCC-MGARCH模型的分析 [J].统计与信息论坛,2012,27(1).
[25]张天顶.通货膨胀与通货膨胀不确定性——基于中国数据的实证研究 [J].西部金融,2012,(7).
[26]申世昌,熊涛.EGARCH(1,1)模型对上证指数与成交金额波动性的实证研究 [J].西南师范大学学报(自然科学版),2016,41(3).
[27]张雪莹.股市与债市的相关性分析 [J].山东工商学院学报,2005,(5).

