三维石墨烯-碳纳米管复合结构热导率的分子动力学模拟

于泽沛，冯妍卉，2，冯黛丽，2，张欣欣，2

（1 北京科技大学能源与环境工程学院，北京100083； 2 北京科技大学冶金工业节能减排北京市重点实验室，北京100083）

引 言

随着电子技术的不断发展，电子元器件体积不断缩小，而其工作频率及集成度却在不断提高，这就对电子元器件的散热提出了更高的要求。电子元器件的散热方式主要是通过导热介质将热传递给散热器，并通过进一步的风冷或者水冷的形式对散热器进行散热。而如何提高电子元件与散热器之间的散热效率，寻找高效的导热介质，使得电子元件能够稳定高效长时间的工作，成为当今研宄的热点[1-10]。

碳材料是一类具有优良传热等特性的材料[11]，而碳纳米管及石墨烯是其中更具代表性的材料，自问世以来，这两种材料因具有极其优良的传热特性引起了学术界的广泛关注[12-15]。但是由于这两种材料的热导率具有明显的各向异性，所以其应用得到了很大限制。2008 年Froudakis 等[16]首次提出三维石墨烯-碳纳米管复合结构结构(3D graphene-CNT hybrid structure, GCHs)，并探究其在氢气储存领域的应用。这种结构不仅弥补了石墨烯及碳纳米管在传热方向机械特性的弱势，还兼顾了二者的优良传热特性。随后大量学者针对这种结构开展不同领域的探索和研究[17-23]。

2013 年，Park 等[20]研究了GCHs 的传热特性，研究结果表明此三维纳米结构具有良好的面内热导率和法向热导率。Loh 等[24]研究表明长波长法向声子模式对GCHs 热传导贡献显著。此外，Loh 等[25]使用分子动力学方法研究了GCHs 机械应变对界面处声子动力学的影响。2014 年，Kamaliya 等[26]研究出了一种可以大规模制备PGNs 的方法，并对其光电特性进行了探讨。2017 年，Zhang 等[27]针对GCHs 不同形状的锥型界面开展研究，表明锥型界面的热导率高于垂直界面。虽然近年来GCHs 的传热特性引起很多研究者的关注[28]，但是其微观的传热机理还不明确，碳纳米管的添加对整体传热的影响，其相关理论还不够完善，需要进一步的研究。

本文采用非平衡分子动力学方法模拟了GCHs的热导率，通过声子态密度和重叠能等机理分析方法探究了GCHs 内部的传热机制以及碳纳米管的添加对传热的影响。本研究将利于GCHs 的应用及高热导材料的开发，为三维纳米材料传热机理提供新的启示，以拓展高导热三维纳米材料的设计与应用。

1 模型与模拟方法

1.1 模型的构建

为了将多层石墨烯与碳纳米管(carbon nanotube，CNT)以化学键的方式相结合，先在石墨烯片层上挖掉略大于CNT直径的孔洞，然后将CNT放到对应的位置，通过重新成键的形式将二者结合起来[19]。

本文采用Materials Studio 软件建模。首先，使用软件自有的石墨模型，优化计算得到30.1 Å×48.8 Å(1 Å=0.1 nm)、层间距24 Å 的多层石墨烯单晶结构，然后在石墨烯每一层上挖去相应孔洞得到多层石墨烯纳米网的单晶结构，之后将长度为23.5 Å 的(6,6)扶手椅型CNT 添加移动到孔洞位置，重新成键得到三维GCHs 的单晶结构。沿着z 方向建立3 晶胞的超晶胞结构，如图1所示。

1.2 模拟方法

本文采用非平衡分子动力学的方法模拟计算GCHs 的热导率。该方法的热传递是通过对体系施加扰动的方式来实现的，通过计算获得热流与温度梯度，然后依据傅里叶导热定律得到模拟对象的热导率

式中，J为热通量；λ为热导率；∇T为温度梯度。

图1 GCHs单晶胞及其3晶胞结构Fig.1 Single lattice and 3 lattices structure of GCHs

本文所采用的非平衡分子动力学方法通过外加热流的形式来对模拟体系施加扰动，即将模拟体系划分为热端、冷端和热传递区域三部分，每间隔一定的模拟时间就从冷端取走部分能量，并同时从热端注入等量的能量，从而使模拟体系产生恒定的热流，而热流则由注入和取出的能量来决定。系统通过改变冷端和热端原子的动量来实现能量转移。一定的模拟时间后，模拟体系达到平衡状态，系统通过统计所有原子的能量和温度获得模拟体系的温度梯度，进而通过傅里叶定律求出热导率。与平衡分子动力学方法相比，非平衡分子动力学方法的优势在于计算速度快，体系不易温漂，但是其模拟的难点在于选择合适的统计层数，只有当统计层内部原子的分热流均处于平衡状态时，才能统计所有原子的能量和温度。

由于本文的研究对象由碳元素组成，因此采用Tersoff势函数[29]来约束C—C键。

1.3 模拟过程

本文所有的模拟计算均在开源软件LAMMPS[30-32]中进行，为了防止体系过分漂移，将z轴两端的两层原子进行固定，同时将两端除固定原子外的部分原子分别作为冷端和热端。首先，在NVT(体积恒定，温度恒定)系综下对整个模拟体系进行能量最小化，得到优化后的稳定结构。然后在NVE(体积恒定，能量恒定)系综下，模拟温度300 K，时间步长0.1 fs，模拟步数1500 万步，共计1.5 ns 的模拟时间。如果模拟体系最终的平衡温度接近300 K，则证明体系处于平衡状态。整个模拟过程采用Nose-Hoover[32-33]恒温恒压方法来控制体系的压强与温度。为了保证计算的准确性，两个模拟盒子大小的体系均进行了3次计算并取平均值。

2 结果与分析

2.1 热导率的计算

系统平衡以后，得到两个模拟体系平衡状态下的温度分布，如图2所示。利用傅里叶导热定律的公式来计算热导和界面热阻[34]

式中，κ 为体系的热导率；J 为热通量；A 为沿热流方向的横截面积；∇T 为冷端与热端之间的温度梯度。

式中，R为界面热阻；ΔT为界面处温度阶跃。

体系中，沿Z轴，也就是垂直于石墨烯片层方向所施加的热流为1 eV/ps，晶胞沿z 轴方向的横截面积即为热流方向的横截面积，根据式(2)计算得到GCHs 的热导率为(1.42±0.05)W/(m·K)。相比较多层石墨烯的层间热导率，提升了一个量级。界面热阻为2.15×10-9(m2·K)/W，相比碳管的接触热阻6.46×10-8(m2·K)/W 降低了一个量级[34]，证明碳纳米管的存在为GCHs 法向方向的传热构建了传热通道，提高了其法向热导率。此外，从图中可以看出，GCHs 温度的阶跃主要集中在石墨稀与碳纳米管的界面处，说明法向传热的限制在于石墨烯片层和碳纳米管界面形变的存在。这是由于声子由碳管传递到石墨烯再传递到碳管这一过程中，声子能量会产生重新分配，振动的不匹配影响了声子能量的传递；界面处出现较强的声子散射，尤其是低频声子散射，而低频声子的平均自由程比高频声子大，故其对热导率的贡献更大，其散射越强，热导率就越低。

2.2 振动态密度分析

纳米材料的热导率与晶格的振动相关，振动态密度(vibrational density of states，VDOS)可以得到原子的振动状态及晶体结构中能量的分布，从而可以得到限制能量传递的原子或结构。本文通过对比计算GCHs 和多层石墨烯的VDOS 探究了热导率与结构之间的关系。β 类原子的VDOS(DP,β(ω))是通过其速度自相关函数(velocity autocorrelation function，VACF)的傅里叶变换和权重因子cβ得到。VDOS 的计算公式如下[13,35]

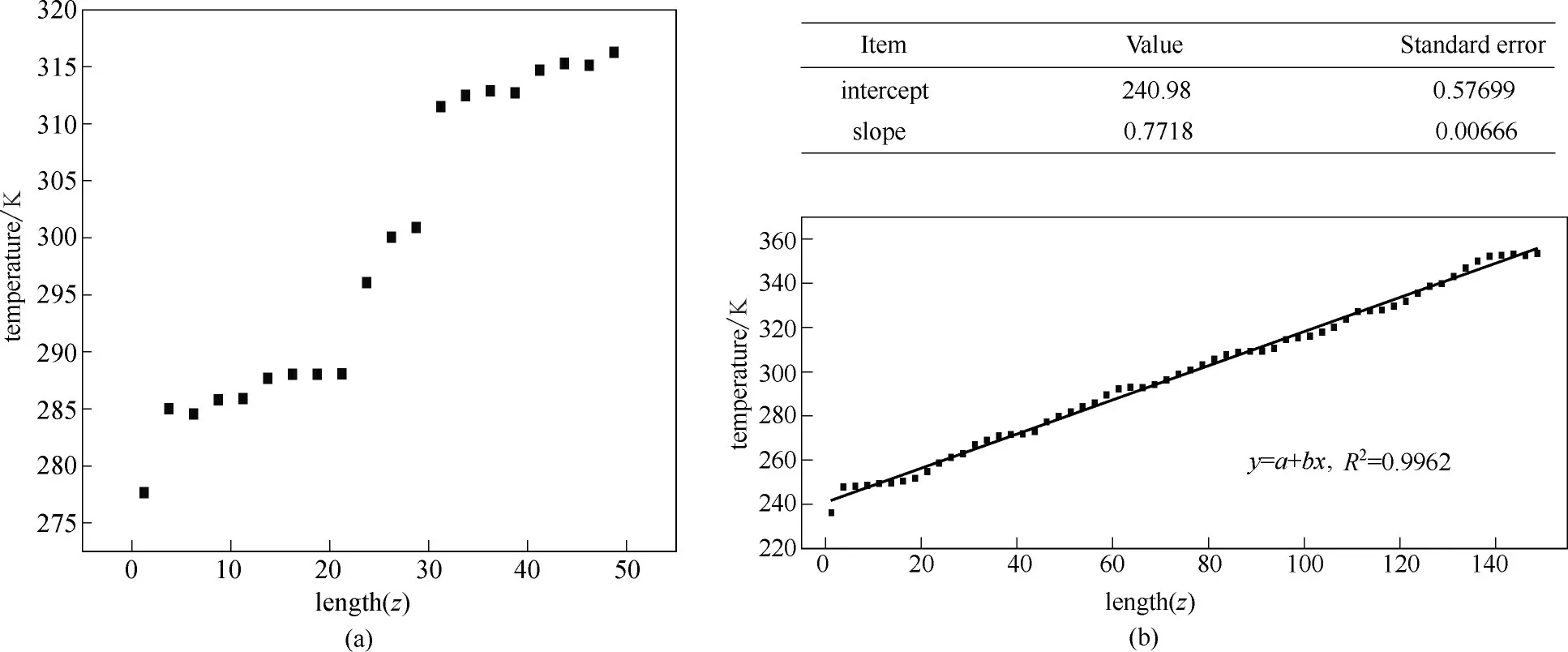
图2 单晶胞GCHs(a)和3晶胞GCHs(b)的温度分布图(300 K)Fig.2 Temperature distribution of single lattice GCHs(a)and three lattice GCHs(b)(300 K)

式中，ω为频率。

式中，Γβ为β 类原子的速度自相关函数；uiβ(t)为β类原子的速度；〈〉为时间平均。

图3 为GCHs 的VDOS 计算结果。从图中可以看出，相比较多层石墨烯，GCHs 的VDOS 的低频区原子有所降低，而在中高频区出现多个峰值，证明有更多的声子被激活参与振动，进而使得其层间热导率得到大幅度提升。对图3 数据进行进一步处理，得到不同频率段对GCHs 热导率的贡献，其结果如图4 所示。从图中可以看出，虽然中高频声子得到不同程度激发而参与传热，但是激发的0～30 THz的低频声子依然占据主导，对导热贡献最大。

2.3 重叠能分析

在VDOS 定性分析的基础上，为了定量分析GCHs 热导率与结构之间的关系，本文引入了重叠能的概念，其计算公式如下[31,36]

式中，Eoverlap为重叠区域go(v)的重叠能；h 为Planck 常 数；v 为 频 率；exp(hv / kBT)- 1 为Boltzmann 分布；T 为热力学温度；kB为Boltzmann 常数。重叠能越高表明两种原子类型的声子振动越协调，越有利于能量的传递。其计算结果如图5 所示，红色为碳管和界面区域的重叠能，蓝色为石墨烯片层与界面区域的重叠能。

图3 GCHs及多层石墨烯的归一化振动态密度(300 K)Fig.3 Normalized VDOS of GCHs and multilayers graphene(300 K)

图4 GCHs不同频率段声子对热导率的贡献(300 K)Fig.4 Contribution of phonons at different frequencies to thermal conductivity of GCHs(300 K)

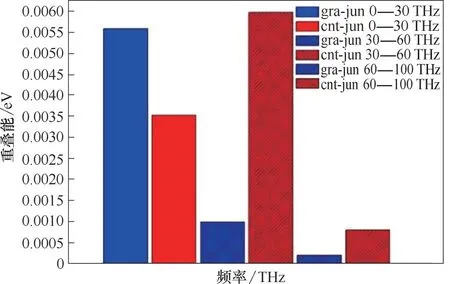
图5 GCHs不同区域不同频率段的重叠能Fig.5 Overlapping energy of different frequency in different regions of GCHs

可以看出，在热导率贡献占主导的低频声子中，石墨烯片层和界面区域的重叠能大于碳管与界面区域的重叠能。这与上述计算中温度分布在界面处出现阶跃，热阻陡增的结论相一致，并进一步明确，是碳管-界面区域的声子能量局域化最为严重，声子振动的协调性最差，影响了能量的传递，是限制GCHs热导率的关键因素[37]。

3 结 论

本文基于非平衡分子动力学模拟了三维石墨烯-碳纳米管复合结构的法向热导率。

(1)其法向热导率为1.42 W/(m·K)，相比多层石墨烯的法向热导率提高了一个量级，其界面热阻为2.15×10-9(m2·K)/W，相比碳纳米管的接触热阻降低了一个量级，证明碳纳米管的存在为石墨烯层间构建了传热通道，提高了其层间热导率。

(2)通过温度阶跃位置对应结构，发现界面是热阻产生的主要原因，界面形变的存在却影响了热导率的进一步提高。

(3)通过计算多层石墨烯和GCHs 的振动态密度，发现碳纳米管的添加使得更多频率范围的声子得到了激发，进而提高了法向热导率，但是对热传导起主导作用的依然是低频声子。

(4)通过计算界面结构的重叠能，探究了三维石墨烯-碳纳米管复合结构结构能量的传递及声子的局域化情况。在低频声子区域，碳纳米管与界面原子的振动不匹配度，是影响热传导的最主要的限制因素，进一步验证了同一元素的三维结构中，界面处的形变是限制热量传递的主要因素，进而为后续高热导材料的改进及开发提供了一定的方向性指导：同种元素的三维结构中，界面突变越少，界面越平滑，结构原子类型越少，原子间振动的协调性越好，声子散射越少，能量局域化的程度越低，热导率就越高。