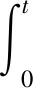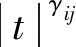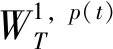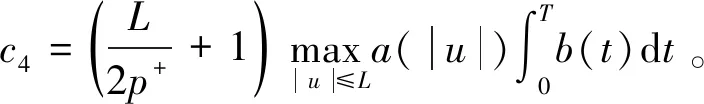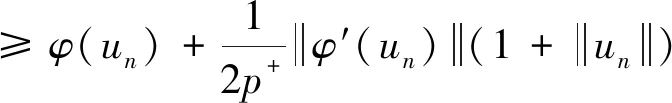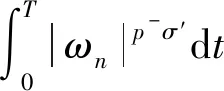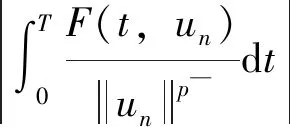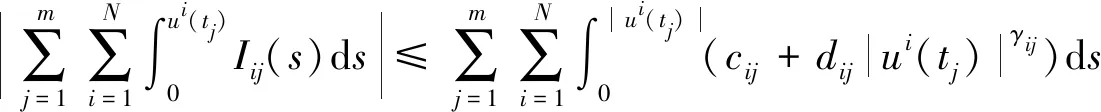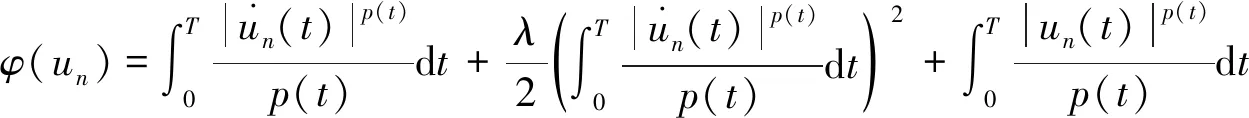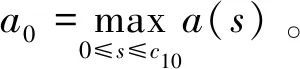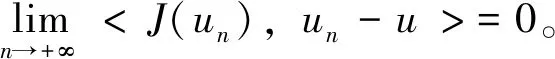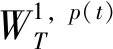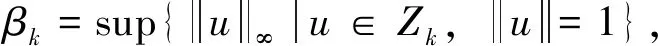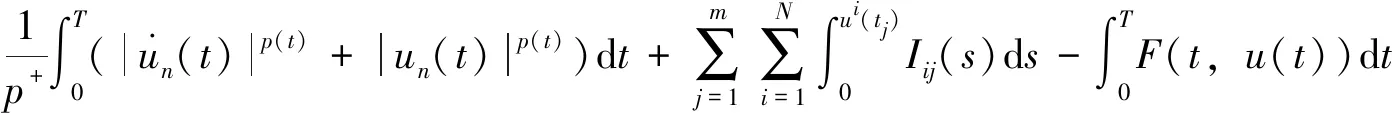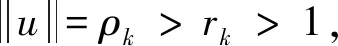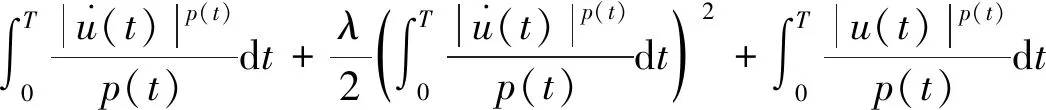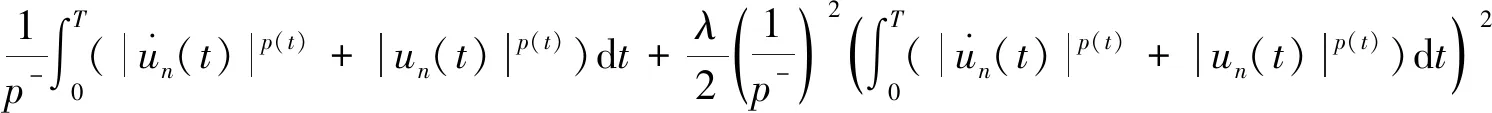变指数脉冲微分系统的多重周期解*
张申贵
(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)
本文中, 研究二阶脉冲微分系统

(1)

设Iij:R→R连续,tj表示脉冲发生的时刻, 且t0=0 问题(1)具有以下三个特点: 首先,问题(1)中带有脉冲效应项。在许多科学领域的研究中都呈现出脉冲现象, 例如有毒杂草在牧区草场中的季节性爆发过程, 生物神经元的输入过程, 注射药物在人体中的浓度变化过程等,脉冲微分方程考虑到瞬时突发现象对系统状态的影响。近年来, 脉冲微分方程吸引了很多学者的关注, 已有一些研究结果,如文献[1-6]。 当λ=0,Iij(t)=0时, 一些学者研究了p(t)-Laplace 系统周期或同宿解的存在性[10-15]。特别的, 当p(t)=2时,非线性项满足(AR)型超线性条件, 即存在μ>2,L>0使得 0<μF(t,u)≤(▽F(t,u),u),对所有|u|≥L和t∈[0,T]成立时,文[11]利用山路定理得到了p(t)-Laplace系统周期解的存在性定理。由(AR)条件可推出非线性项在无穷远处关于变量u是超线性增长的, 该条件可以保证作用泛函的(PS)序列是有界的, (AR)条件已应用于非线性微分方程的研究中,但是许多超线性函数并不满足(AR)条件[16-19]。 记p(t):[0,T]→R+为连续函数,定义变指数 Lebesgue 空间 (2) 引理3[20](喷泉定理)设X为Banach空间,X=Zk⊕Yk,dimYk<+∞。若泛函φ∈C1(X,R),满足:φ(0)=0,φ(u)=φ(-u),且 则泛函φ有一列趋向于+∞的临界值。 假设以下条件成立: (F0) 对任意的u∈RN,F(t,u)关于变量t可测;对a.e.t∈[0,T],F(t,u)关于变量u连续可微,且存在函数a∈C(R+,R+)和b∈L1([0,T];R+),有|F(t,u)|≤a(|u|)b(t);|▽F(t,u)|≤a(|u|)b(t),对a.e.t∈[0,T]和所有u∈RN成立。 (F1) 设存在常数c1>0,c2>0,L>0及σ>1,使得 (F3) 设F(t,0)=0,F(t,u)=F(t,-u),对a.e.t∈[0,T]和所有u∈RN成立。 对于i∈{1,2,…,N},j∈{1,2,…,m},Iij(t)满足下列条件: (I3) 对∀t∈R,Iij(t)都是奇函数。 本文的主要结果如下: 定理1 设条件(F0)-(F3),(I1)-(I3)成立,则问题(1)有无穷多个解{uk}k∈N满足:当k→+∞时,有φ(uk)→+∞。 证明下面利用喷泉定理(引理3)证明定理1。下面用ci,i=0,1,2,…表示不同的正常数。 (3) (4) 由条件(F0)和(F1)-(i),可得 (5) (6) 联合式(5),式 (6), 有 (7) 结合式(4), 当n→+∞时, 有 (8) 由式(6),条件(F1)-(ii),可得 (9) 由式(8),式(9), 并利用Hölder 不等式, 当n→+∞时, 有 (10) (11) 由Iij(t)的连续性, 当n→+∞时,有 由条件(F0),当n→+∞时,有 (12) 第3步证明泛函φ满足引理3中条件(iii)。 注意到dimYk<+∞,由有限维空间范数的等价性,有 (13) 由条件(F0)和(F2),对于∀ϑ>0,存在c13>0,使得 (14) 对a.e.t∈[0,T]和所有u∈RN成立。 综上, 泛函φ满足引理3中所有条件, 由引理3知, 泛函φ有一列临界点{uk}k∈N满足: 当k→+∞时,有φ(uk)→+∞, 从而问题(1)有无穷多个解{uk}k∈N满足:当k→+∞时,有φ(uk)→+∞。 取p(t)=2,N=4,t1=1,t2=2,令 其中i=1,2,3,4,j=1,2,则Iij(t)满足条件(I1)-(I3)。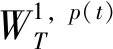
1 准备知识









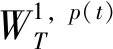



2 主要结果