基于PSF估计的电阻阵列非均匀校正

李赜浩，廖守亿，张作宇

基于PSF估计的电阻阵列非均匀校正

李赜浩，廖守亿，张作宇

（火箭军工程大学 控制科学与工程系，陕西 西安 710025）

电阻阵列红外仿真技术至今已发展为一项较为成熟的红外成像仿真方法，不仅像元规模越来越大，制造工艺水平也越来越高。尤其是国外，已研制出大规模商用电阻阵列器件，并在众多武器系统研制过程中得到了应用；国内在该方面同样取得了较大的进步，但是在传统的非均匀测试方法上国内研究还存在一些遗留问题未得到很好的解决。如实验中出现的莫尔条纹、边缘效应、映射与对准等相关难题很少有研究者提出详尽可行的处理措施。本文针对莫尔条纹和边缘效应问题，提出了一种基于点扩散函数估计的迭代非均匀性测试方法，实现了条纹干扰和边缘效应的去除。此外，本文对于映射比大于1:1的情况进行了仿真验证，对比了不同映射比和不同非均匀程度对校正效果的影响，给出了进行下一步实验的理论基础。

点扩散函数；莫尔条纹；全屏测试法；试验估计法；映射比

0 引言

红外成像目标仿真技术包括红外图像的生成和投射两方面，投射技术中又以电阻阵列技术和数字微镜技术最具有发展潜力。数字微镜系统（Digital Micromirror Devices）具有分辨率高、无死像元、均匀性好等特点[1]，但国内对DMD的研究起步较晚，同时DMD也存在温度范围低、对比度不高等特点。此外，由于其工作原理限制，在用于扫描成像体制的红外导引头半实物仿真时难以实现同步，且具有长波衍射的缺点。电阻阵列式红外景象投射器更加适合国内需求，具有更广阔的应用市场。尤其是悬浮薄膜式电阻阵列具备较宽的温度范围和辐射光谱，能够实现在高于200Hz帧频下的工作，具有低功耗、低串音、低闪烁、温度范围大、对比度高等特点，所以电阻阵列技术在红外成像仿真领域有着很高的受欢迎程度。国产电阻阵列的研发也在持续推进，512×512规模的电阻阵列已研制成功。但是，由于电阻制造工艺等因素，每个电阻器件在同一驱动下的响应曲线通常是不一致的，即电阻阵列各辐射元的实际辐射输出之间存在差异，从而造成热图像的不均匀[2]。为解决成像质量问题，非均匀校正技术应运而生。美国、澳大利亚、英国等国家的该项技术已达到了很高水平，实现了较好的投射效果，大大推动了其红外成像仿真技术的发展。

非均匀校正技术中稀疏网格法（Sparse grid）和全屏测试法（Flood）是当前的研究主体，前者提出时间较早，此后的许多方法都是以其为基础，从相同的校正原理出发加以改进和拓展。全屏测试法在稀疏网格法基础上不仅大大提高了校正效率，同时具备较高的准确性。Flood法的难点在于测量时数据的准确提取和处理，由于期间不可避免地会引入噪声、边缘效应、莫尔条纹等的影响，所以选择合适的测试方式十分重要。

Leszek Swierkowski和Owen M. Williams[3]介绍了一种利用点扩散函数（Point Spread Function）的方法用以提高非均匀校正的效率，该方法被应用到电阻阵列和红外热像仪有良好的1:1映射的场合。Leszek Swierkowski等人[4]还提出了在映射比非1:1条件下基于PSF估计和利用子像元细分的非均匀校正方法，适用于系统因存在对准偏差而出现莫尔条纹的情况。Leszek Swierkowski、Robert A. Joyce和Owen M. Williams[5]于2007年为了解决与采样和辐射元细节相关的问题，强调了应用精密的映射和对准算法与控制从莫尔条纹和子像元影响中分离残余非均匀性的投影技术的重要性，并提出半Flood法的非均匀校正过程。2008年，Owen M. Williams等[6]进一步提出分离次图像的方法，既能成功消除莫尔条纹，又能大大降低残余非均匀性，并且讨论了通过选择映射比进而控制莫尔条纹状态的问题。近年来，国内的苏德伦、杨春伟、朱岩等人[7-9]也曾论述过基于PSF估计的非均匀校正，在一定的前提条件下改进了已有的校正方法，取得较好的仿真效果。但是实用性不强且未对不同映射比下莫尔条纹的影响程度进行分析，也未对PSF估计过程提出详尽的实验步骤。

在以往的研究中，获知PSF的情况下能更好更快地实现非均匀校正，然而实际往往无法得知其准确的参数信息。因此PSF估计的近似程度决定了校正效果的好坏，如果能实现精确地估计则大大降低了非均匀校正难度。本文针对莫尔条纹问题，采用试验估计法，确保了在一定的估计误差范围内得到PSF，最后结合全屏测试法的迭代测试，实现了精确的非均匀校正。

1 非均匀校正原理

1.1 莫尔条纹

1.1.1 像元填充因子

实际的辐射像元结构不仅仅只有一整块发热电阻，还有电容、MOS晶体管[10]。电阻作为发热元件是辐射的主体部分，通常电阻的位置在每块像元的中央区域，所以辐射面不是整个像元单元，而只有一部分。以悬浮薄膜电阻阵列为例，它由于采用了立体像元结构，其填充因子往往可以达到50%以上[11]。

如果将单个像元继续细分，假设能分为×个子像元，其中仅有中间的×个子像元发亮（＜），则每个像元辐射情况可如图1(a)所示，发亮部分为像元中间区域。因此当电阻阵列和红外热像仪未实现精确像元对准时，探测像元容易采样到辐射边缘的暗区域，所探测到的图像就会出现如图1(b)类似的“棋盘模式”，又被称为莫尔条纹。

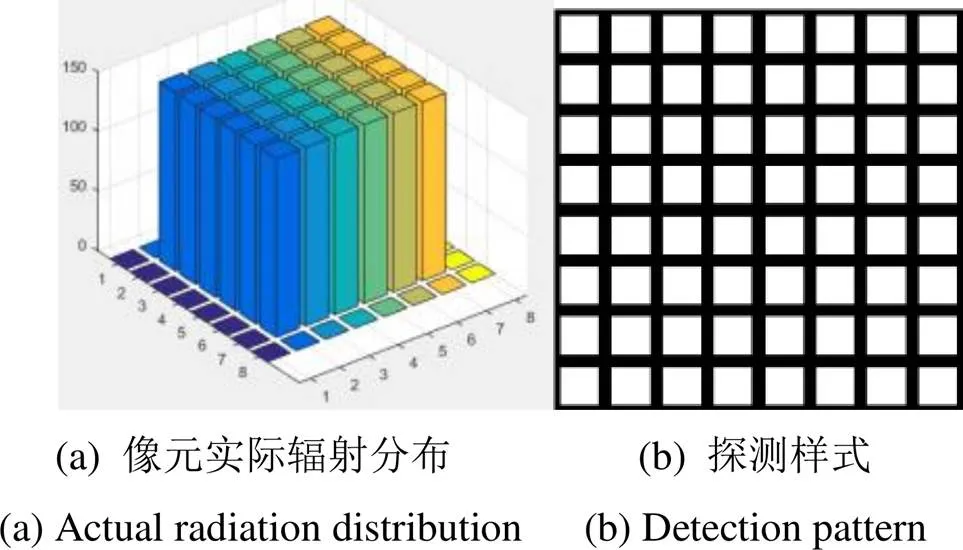
图1 电阻阵列像元实际表现

1.1.2 映射比

单个辐射像元对应的成像像元的个数为其系统的映射比。假设电阻阵列和成像平面均为正方形，令投射图像规模为1×1像元，探测图像规模为2×2像元，则成像仪对投影仪的映射比表示为：

＝2/1(1)

当映射比等于1:1时，投射图像与探测图像尺寸相同，则容易实现像元的对准，即辐射像元与探测像元中心对准，从而保证使得每一个辐射元的质心在热像仪图像中能够精确定位而且那一点的强度可以通过周围相邻处的双三次插值计算得到。然而实际情况中，投射阵列与探测阵列的规模通常是不一样的。随着电阻阵列技术发展，其规模日益增大，而探测阵列要达到同样大小却很困难。所以本文将对映射比非1:1的情况下提出相应的测量方法，以尽可能确保如实地反映辐射亮度。实验中即使实现了映射比为1:1，像元对准也常受到各方面因素的影响，如机械偏差和光学畸变，因此对非一对一采样情况的研究很有必要。

根据上一节描述，每个辐射像元的填充因子均小于1，辐射平面的亮度呈现出周期震荡。那么当像元出现对准偏差时，探测像元的采样值在二维平面上也会出现周期性波动，出现亮暗条纹间隔。当映射比小于1:1时，成像平面小于投射平面，通过平移、缩放等方式调整成像距离与大小以确保全屏显示投射图像，所以就会出现一个探测像元对应多个投射像元，此时探测像元周期性覆盖了最大的波谷区域，图像出现间隔相等的暗条纹；当映射比大于1:1时，情况与小于1:1时相反，探测像元周期性覆盖了最大的波峰区域，图像出现间隔相等的亮条纹，如图2所示。

图2 不同映射比时莫尔条纹表现

1.2 全屏测试法

Flood法是沿用多年的非均匀校正测试方法之一，也是至今研究最多，更具提升空间的测试方法。它拥有效率高、准确度高、实时性好等特点，适合实验中采用。同时该方法也存在算法较复杂、需要光学配准、容易引入干扰因素的问题[11]。光学设备的对准和驱动电压过高都是成为影响其成像质量及亮度测量的外在原因。Flood方法的特点是在测量电阻响应情况时同时点亮整片区域或部分区域，然后可通过逐步迭代，提取出非均匀信息并补偿非均匀性，使得投射图像最终趋于预设亮度。校正过程中如何处理像元之间的能量重叠以及采样噪声的影响和准确获取点扩散函数模型的具体参数是难点。

Flood法还有一个重要特点体现在闭环的迭代过程，通过探测到的像元辐射灰度值与标准输入灰度值作比较得到增益因子，该增益因子通过每一次迭代得到修正，直到增益稳定不变时即能使得此补偿下的输入有符合标准的输出，如图3是经典盲迭代步骤。

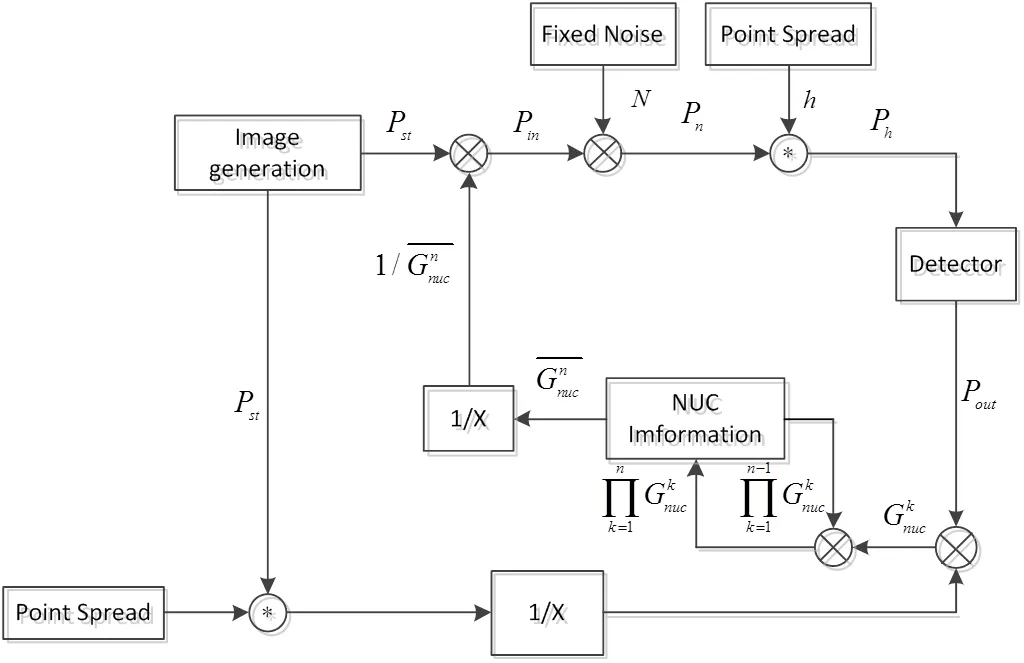
图3 盲迭代测试法流程

根据全屏测试法的原理，输入端给定一帧均匀的输入st，仿真测试中均以灰度图数据为运算对象。将像元非均匀性看做固定的高斯噪声，那么投射图像P可表示为：

P＝in×(2)

在像元的探测、成像过程中出现的退化现象，可通过与点扩散函数卷积来表征图像模糊：

P＝P*(3)

迭代过程的增益nuc可由探测到的图像out对原始输入的均匀图像做商得到，如果探测图像与投射图像大小不同，则在计算增益后必须经过图像插值的过程，还原成原图像大小。一般情况下增益可表示为：

nuc＝out/st(4)

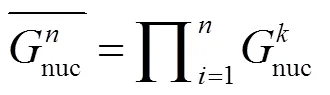
2 试验法估计PSF

在图像复原中，估计PSF的方法主要有观察法、试验法、数学建模法。然后将退化的图像通过与得到的PSF经过去卷积过程实现图像的复原。本节采用试验法作为研究方法，没有严格的实验条件需求。本章以MATLAB仿真模拟试验法，得到一个较准确的估计。

图像退化模型可表示为：

(,)＝(,)*(,)＋(,) (6)

式中：(,)为原始投射图像；(,)为噪声。暂不考虑观测噪声的影响，那么我们将模型简化为：

(,)＝(,)*(,) (7)

试验中可点亮单一像元，即对一个小亮点成像，得到其退化的冲激响应。该点驱动电压尽可能高，以便降低环境噪声的影响。然后对该图像进行傅里叶变换，得到：

(,)＝(,)×(,) (8)

(,)＝(,)(,) (9)

式中：(,)为一个描述冲激强度的常量。

而后对该等式进行傅里叶逆变换，获得粗略估计的(,)。因为电阻阵列的非均匀性，每个像元的冲激响应存在差异，所以只取一个点试验不具有代表性。因此多选几组测试点计算(,)，取其平均值以减少误差：

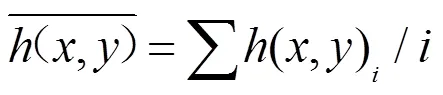
通过与设定的PSF数值作比较，该误差大小能够满足非均匀校正仿真结果达到很好的收敛水平。

该方法的好处是不用建立退化函数的模型，也无需任何先验知识，因此避免了建模不准确带来的误差。这里只需利用傅里叶逆变换得来的数组信息与投射图像的灰度值信息进行盲目去卷积过程即可。若要考虑观测噪声引入的退化，则加入自适应滤波环节即可实现去除干扰。从理论上来看，试验估计法具备较高的准确度，原理简单，易于实现。在设备条件完善、人员操作合理的前提下，该方法是更好的选择。

3 改进的非1:1映射比下的全屏非均匀校正

3.1 莫尔条纹模式生成

为了计算非均匀校正过程中的增益，需要计算机生成具有莫尔条纹形式的标准输入图像，以其作为探测图像数据的运算对象。要预测实际的莫尔条纹样式不算复杂，根据光学系统参数和像元尺寸计算映射比例，然后对辐射像元进行子像元细分。子像元的数量选取准则为：在当前映射比例下单个探测像元刚好覆盖到整数个子像元。根据细分后的投射像元得到采样后的图像形式，将其作为提取非均匀信息的基准莫尔条纹模式，莫尔条纹生成流程图如图4所示。

设将单个投射像元细分为×的子像元，则每个投射像元的辐射能量可表示为由中间(－2)×(－2)个子像元相加得到：

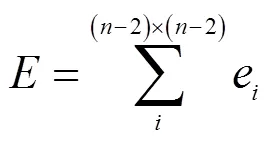
式中：e是每个子像元辐射能量，令其大小相等。

设单个探测像元可分为×个子像元，因此每个探测像元探测值表示为投射阵列的每×个子像元的能量之和：

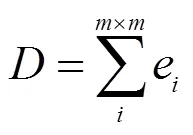
由此得到的探测图像是带有莫尔条纹的。

3.2 消除边缘效应

电阻阵列在投射时辐射能量在探测器平面上分散，以致于边缘辐射像元的输出扩散到采样区域之外，且周边像元又得不到足够能量的补充，所以在探测时的灰度值会比中间区域的要小许多，其中4个角像元灰度值最小，如图5(a)所示。因此经过非均匀校正后，更多地补偿了周边像元的输入，导致其响应自然就比中间区域校正后要高，出现“过校正”的现象，如图5(b)。

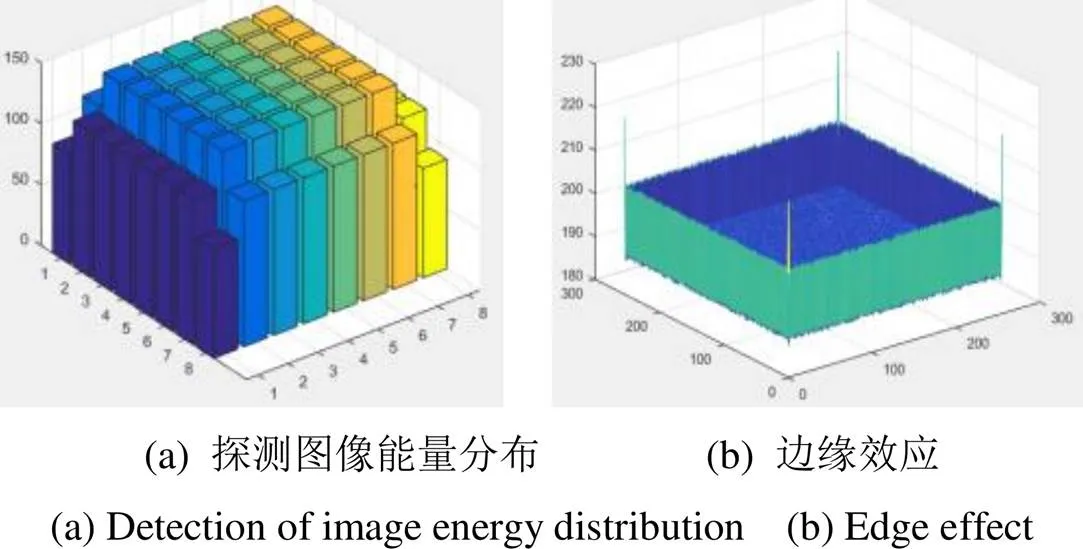
图5 边缘效应来源

利用估计所得到的PSF生成带有莫尔条纹标准输入下的退化图像。这样实现了与探测图像相似的退化性，边缘像元能量得到了同样程度的衰减，因此在迭代过程中，边缘像元计算而来的增益不会偏大，使得相应的驱动电压补偿值趋向合理的范围，从而得到正常的边缘校正图。

这样不仅提高了校正效率，且无需计算PSF的逆算子，如文献[12]，则减少了误差的累积，更具实用性和拓展性。但仅通过该方法得到校正后图像也并不是十分精确的，经过仿真验证图像会出现整体亮度偏低或偏高，这是因为PSF的估计误差引起的。

3.3 基于PSF估计的迭代校正

如图6是改进的迭代测试复原方法，由计算机生成红外灰度图像指令st，通过数据转换将灰度值转换为可以驱动电阻阵列的电压信号。这个转换过程本质很简单，只要将每一个灰度等级与等效黑体温度对应，而电阻阵列的驱动电压与等效黑体温度之间也是一一对应的：

＝()＝3＋2＋＋(13)

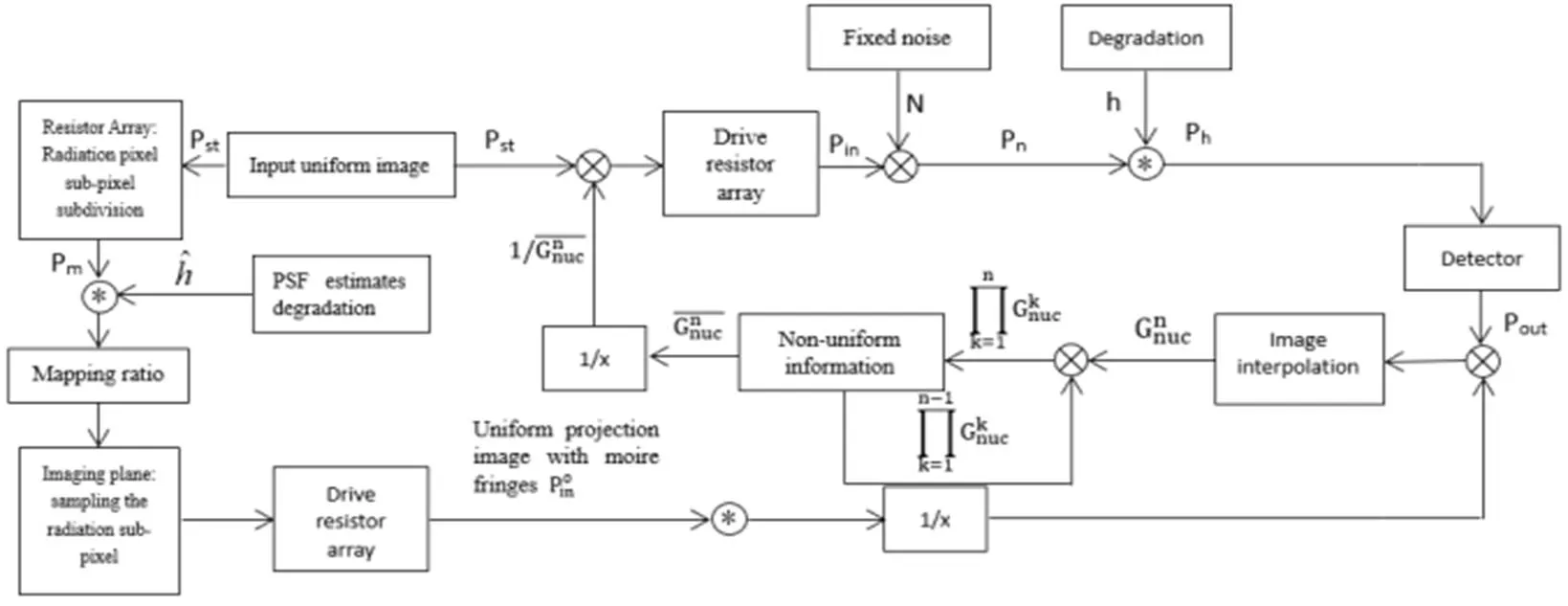
图6 基于PSF估计的改进全屏迭代测试

等效黑体温度与驱动电压的关系可通过测量电阻元平均响应得到，易知它是一个复杂的非线性曲线，经验表明，其响应特性可用如式(13)的高次多项式拟合：

gray＝()＝(14)

将等效黑体温度在0～255范围内分级，从而得到其与灰度值的对应线性关系，如式(14)，gray为灰度值：

gray＝() (15)

这样，通过一定的对应取值和电阻阵列的响应曲线，就可以将灰度图像转换为电压数据。同时，因为各个辐射电阻元的固有属性和成像原理，投射的图像存在亮度不均匀和退化的干扰，为了提取其非均匀信息需要先经过图像的复原，首先生成由估计的PSF退化的输入图像in0。为了准确提取，要生成与探测图像形式相似的输入：

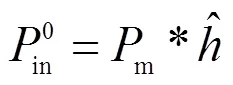
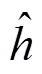
而后以探测图像除以莫尔条纹形式的标准退化图像in0，又由于采样图像的尺寸与投射的不同，增益图像矩阵需经过图像插值，如式(17)。这里进行双三次插值，从而得到所需增益nuc：

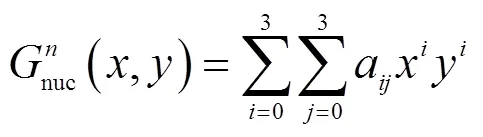
输入的灰度图像数据除以增益，相当于对驱动电压进行了修正。经过若干次迭代后，当增益基本趋于定值时，投射图像灰度值此时也趋于符合输入要求的图像灰度值，非均匀程度大大减弱，实现了非均匀校正。

该方法由盲迭代拓展而来，充分体现出其算法的优势。非均匀信息仍认定为乘性噪声，且在数据处理上以乘除法为主，虽然在收敛速度上不如现有方法所用的加减法，但收敛程度同样很高，且校正过程更简单，对PSF的估计误差有更大包容度。

4 仿真验证及分析

在文献[13]中作者已表明映射比小于1:1时的非均匀校正效果不如映射比大于1:1时好。若映射比例小于1:1，采样图像的空间分辨率小于投射图像数据，则会导致一部分细节信息的丢失，虽然校正后非均匀性有所改善但效果并不理想。因此，在全屏测试中，当无法实现1:1映射比例时，至少应尽量保证大于1:1的映射比例。所以本节仿真仅验证映射比大于1:1的情况。以256×256电阻阵列为例，每个探测像元可覆盖8×8个子像元。映射比分别设置为9/8、10/8、11/8、12/8，标准输入图像灰度值取150，初始非均匀性设为10%。

从图7中发现当映射比大于1:1时，比值越大，探测子像元越密集，因此探测莫尔条纹数量越多，细节信息越丰富。此时即便去除估计PSF环节，同样能取得良好的校正效果，条纹干扰可以基本忽略，经仿真验证残余非均匀性可达到较低水平，如表2。从图8的仿真结果可以看出随着成像平面的规模增大，映射比增大，非均匀校正的收敛速度更快且程度更高。综上所述，可以认为当对红外目标模拟器进行非均匀校正时，为了得到最好的校正效果，务必保证映射比大于1:1。虽然实际试验中，对大规模的电阻阵列校正可能无法找到更大的成像平面，但可通过调整校正步骤达到映射比大于1:1的要求，如在一次Flood校正中减少点亮的辐射元的个数，即只对一部分迭代，然后结合成整体的图像。图9为校正前投射图像，图10和图9相比较好地消除了莫尔条纹和边缘效应。图11所示是由256×256电阻阵列实际投射的图像，其基本无莫尔条纹影响且均匀性较好，体现出本方法的良好实验效果。

图7 映射比为9/8、10/8、11/8、12/8时莫尔条纹表现

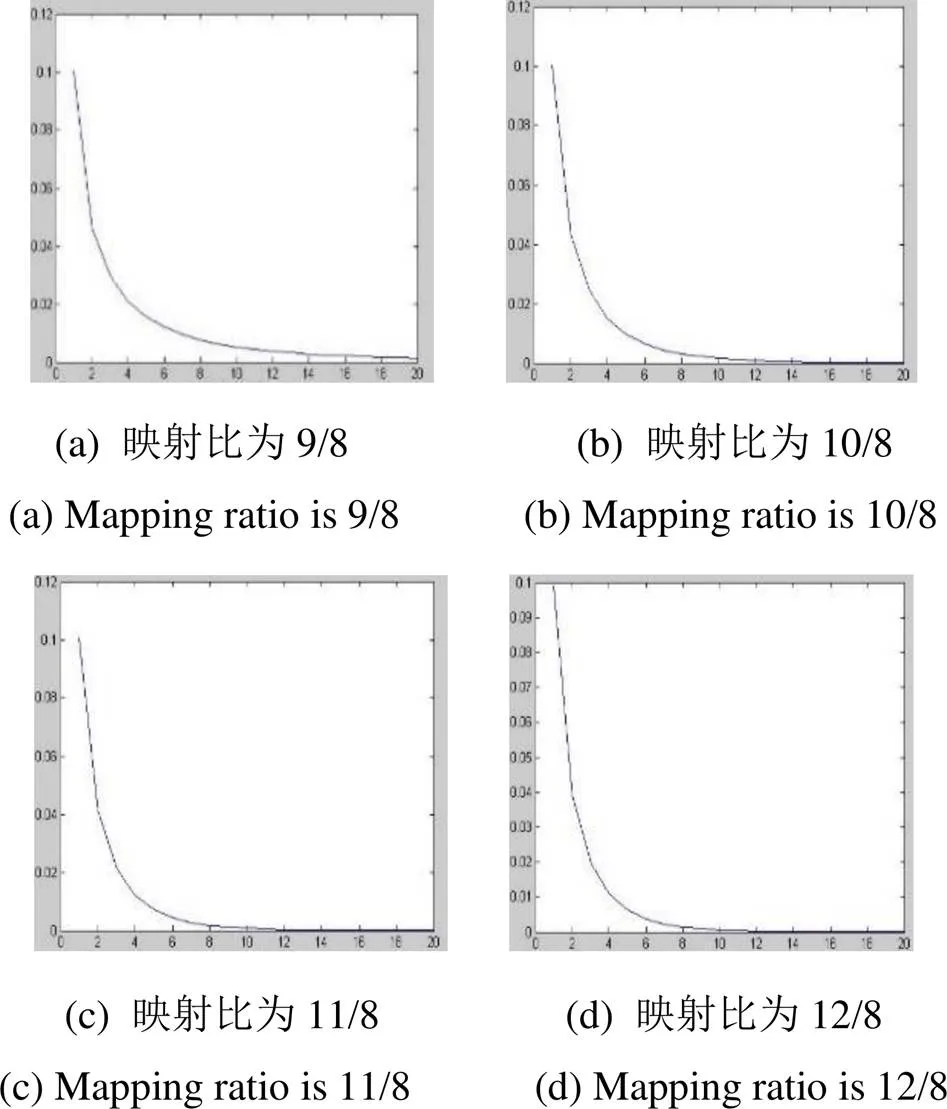
图8 映射比为9/8、10/8、11/8、12/8时校正后收敛水平随迭代次数的变化

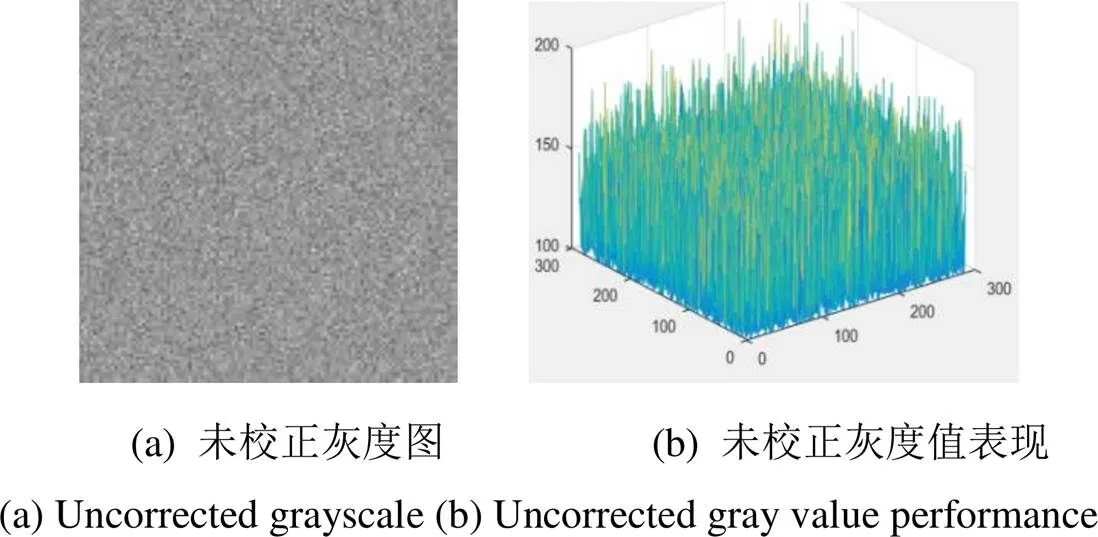
图9 投射图像校正前

当映射比为9/8，初始非均匀性分别为5%、10%、15%、20%时，该算法校正效果如表1所示。

当映射比为9/8、10/8时，初始非均匀性分别为10%时，去除PSF估计环节后校正效果如表2所示。

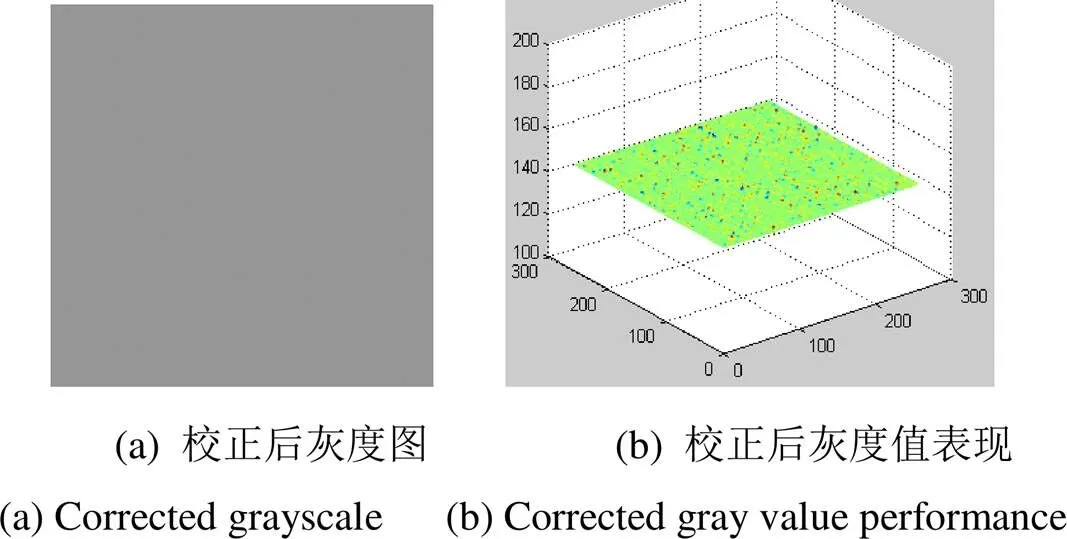
图10 投射图像校正后

图11 电阻阵列实际投射测试图

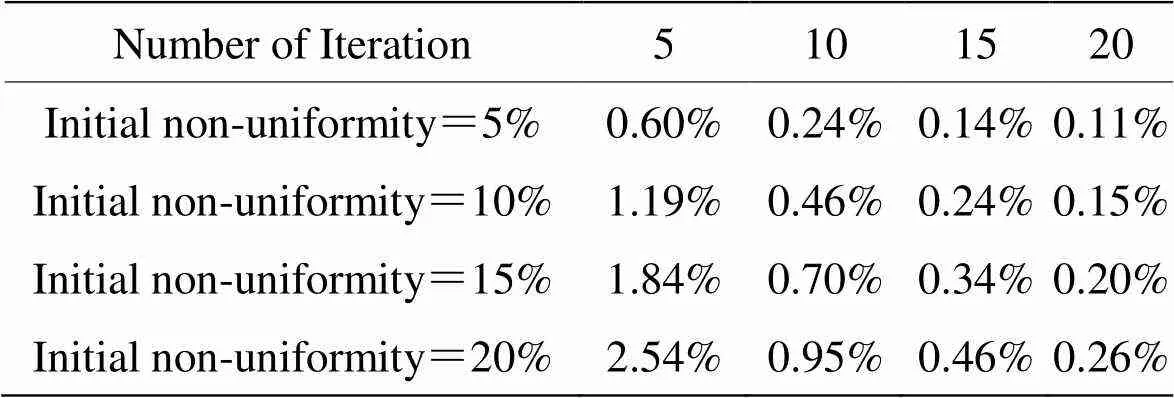
表1 不同初始非均匀程度下迭代校正效果

表2 不同映射比下无PSF估计时迭代校正效果

本改进方法在仿真的基础上体现出了其良好校正效果，主要针对的是解决莫尔条纹干扰等问题，对不同映射比下迭代收敛速度做了简要的分析，并确保能达到较低的残余非均匀性。同时该方法流程比现有方法更加简明，在盲迭代的基础上增加模拟退化和莫尔条纹预测，具有不错的实时性和可操作性。

5 结束语

本文提出的基于PSF估计的迭代测试方法，具备盲迭代法的快速性，较好地解决了非均匀校正过程中带来的莫尔条纹和边缘效应的影响。仿真校正实验表明，其有很好的收敛水平和适应度，体现在不仅功能简单易行，校正误差小，又具有实用价值。下一步将结合工程应用环境，对本文校正方法加以验证和完善，进一步提升校正的准确度和速度。此外，本文方法对优化校正流程，提高实验效率也具有一定的借鉴意义。

[1] 贺敏, 胡以华, 雷武虎, 等. 红外景象投射技术研究[J]. 红外与激光工程, 2008(s2): 17-20.

HE Min, HU Yihua, LEI Wuhu, et al. Research on infrared scene projection technology[J]., 2008(s2): 17-20.

[2] 李艳, 孟庆虎, 吴永刚. 国外电阻阵列非均匀性校正技术概述[J]. 红外技术, 2010, 32(8): 453-456.

LI Yan, MENG Qinghu, WU Yonggang. Overview of foreign resistance array non-uniformity correction technology[J]., 2010, 32(8): 453-456.

[3] Leszek Swierkowski, Owen M. Williams. Search for optimal infrared projector nonuniformity correction procedures: II[P]. Defense, Security, and Sensing, 2000.

[4] Leszek Swierkowski, Owen M. Williams. Search for optimal infrared projector nonuniformity correction procedures: III[P]. Defense, Security, and Sensing, 2001.

[5] Świerkowski L, Williams O M. Resistor array infrared projector nonuniformity correction: search for performance improvement II[J]., 2007, 6208: 73010M-73010M-12.

[6] Robert A Joyce, Leszek Świerkowski, Owen M Williams. Resistor array infrared projector nonuniformity correction: search for performance improvement III[C]//, 2008: 69420N. (doi: 10.1117/12.777785).

[7] 杨春伟, 廖守亿, 苏德伦,等. 电阻阵列非均匀性测试与校正[J]. 红外技术, 2013, 35(6): 345-349.

YANG Chunwei, LIAO Shouyi, SU Delun, et al. Resistance array non-uniformity testing and correction[J]., 2013, 35(6): 345-349.

[8] 苏德伦, 张金生, 廖守亿. 电阻阵列非均匀性测试[J]. 红外技术, 2010, 32(6): 345-348.

SU Delun, ZHANG Jinsheng, LIAO Shouyi. Resistance array non-uniformity test[J]., 2010, 32(6): 345-348.

[9] 朱岩, 许渊, 王连武, 等. 1:1映射情况下电阻阵列Flood法非均匀性校正技术研究[J]. 红外技术, 2010, 32(9): 535-540.

ZHU Yan, XU Yuan, WANG Lianwu, et al. Research on non-uniformity correction technique of resistance array Flood method under 1:1 mapping[J]., 2010, 32(9): 535-540.

[10] 李守荣, 梁平治. 电阻阵列动态红外景像产生器[J]. 半导体光电, 2001, 22(5): 308-312.

LI Shourong, LIANG Pingzhi. Dynamic Infrared Scene Generator for Resistor Array[J]., 2001, 22(5): 308-312.

[11] 苏德伦, 廖守亿, 张金生, 等. 电阻阵列非均匀性校正[C]//先进光学技术及其应用研讨会, 2009: 316-320.

SU Delun, LIAO Shouyi, ZHANG Jinsheng, et al. Resistance array non-uniformity correction[C]//, 2009: 316-320.

[12] Swierkowski L, Williams O M. Advanced flood nonuniformity correction for emitter array infrared projectors[C]//, 2002: 108-119.

Nonuniformity Correction of Resistance Array Based on Estimation of Point Spread Function

LI Zehao，LIAO Shouyi，ZHANG Zuoyu

(Department of Control Science and Engineering, Rocket Force University of Engineering, Xi’an 710025, China)

The infrared simulation technology of resistance array has been developed into an established infrared imaging simulation method, which not only has a larger scale but also employs a higher level of manufacturing technology. Large-scale commercial resistor array devices have been developed and applied in the development of several weapon systems, especially in foreign countries. Domestically, considerable progress has been made in this aspect, but some legacy issues related to research on traditional nonuniformity testing methods have not been well resolved. For example, Moiré fringes, edge effects, mapping, and alignment problems appear in experiments, and few researchers have proposed detailed and feasible treatment measures. In this study, an iterative nonuniformity test method based on point spread function estimation is proposed for solving the problems of Moiré fringes and edge effects. In addition, the simulation verification of the mapping ratio exceeding 1:1 is carried out. The effects of different mapping ratios and nonuniformities on the correction effect are compared, and the theoretical basis for the next experiment in this study is given.

point spread function, moire fringe, flood method, experimental estimation method, mapping ratio

TN215

A

1001-8891(2020)01-0086-07

2019-05-21；

2019-12-31.

李赜浩（1995-），男，湖南岳阳人，硕士在读，主要研究方向为导航、制导与仿真方面研究。E-mail：183435120@qq.com。

航空科学基金（201601U8001）。