例析四边形最值问题的常见题型及其求解策略

广东省佛山市第一中学(528000) 吴统胜 李 维

高考对解三角形部分内容常考查“利用正弦定理、余弦定理、主要的三角公式、基本不等式等知识,通过转化、方程等思想,经过运算、推理、度量边、角或周长、面积和其他伴随要素.”解三角形的实质是将几何问题转化为代数问题即方程问题,故解三角形的核心是方程思想.而四边形最值问题因其综合性强,常作为选择题或填空题的压轴题来考查.常需利用基本不等式、函数观点或数形结合才可有效突破,可以较好地考查考生逻辑思维能力、运算求解能力和创新能力,突出高考的选拔功能.下面笔者举例说明四边形最值问题的常见题型及其求解策略,以期对广大师生在解决此类问题时带来帮助.

题型一 长度最值问题

评析设∠BAC=θ,利用正弦定理、余弦定理直接建立AD关于θ的目标函数,再利用辅助角公式求得最值.

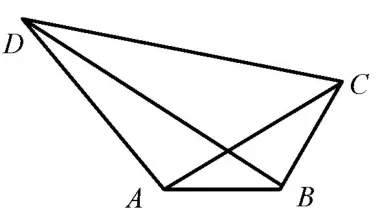
图1

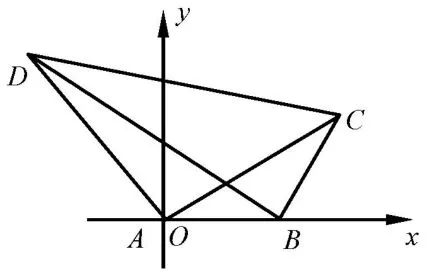
图2

评析建立适当的平面直角坐标系,引入角作为参数,结合复数三角形式乘法的几何意义求出点D坐标,再利用两点间的距离公式表示出AD,进而求得AD最值.研究平面几何中的长度、面积及线线位置问题,有时可以采用解析法使问题得到巧妙解决.

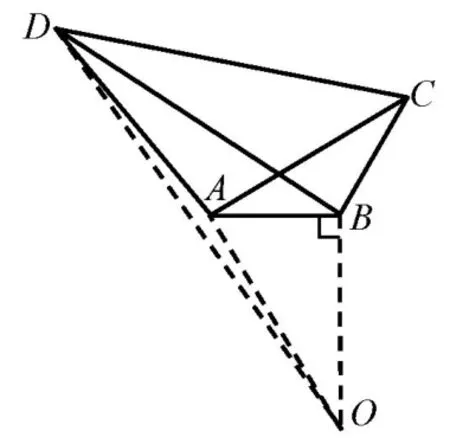
图3

解法3(几何视角)如图3,过B作BO⊥BA,且BO=2,连接OA、OD,则又∠OBD=∠ABC=90◦+∠ABD,所以 ∆OBD∽ ∆ABC,从而即因为OA+AD≥OD,所以当且仅当O,A,D三点共线时,AD的最小值为

评析该解法巧妙地构造了与∆ABC相似的∆OBD,并利用相似三角形的性质得到再由三角形两边之和大于第三边非常巧妙地求得了AD的最小值.

解法4(轨迹视角)由解法3得即点D的轨迹是以O为圆心,为半径的圆,以O为原点,直线OB为y轴建立直角坐标系,设则

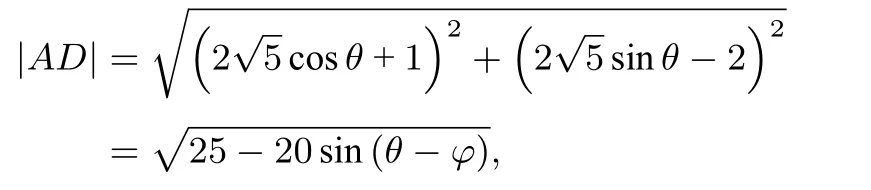
余下同解法2.

评析该解法是从轨迹的视角求最值.

解法5(托勒密定理)托勒密(Ptolemy)定理指出,圆内接凸四边形两条对边乘积的和等于两条对角线的乘积,其推论是在任意凸四边形ABCD中,必有AC·BD≤AB·CD+AD·BC,而且当A,B,C,D四点共圆时取等号.

例2如图4,平面四边形ABCD的对角线的交点位于四边形的内部,当∠ABC变化时,对角线BD的最大值为____.

解析解法1(代数视角,构建边关于角的函数)

设∠ABC=α,∠ACB=β,AC=CD=x(x＞0),在∆ABC中,由余弦定理可得由正弦定理可得也即

在∆BCD中,由余弦定理得

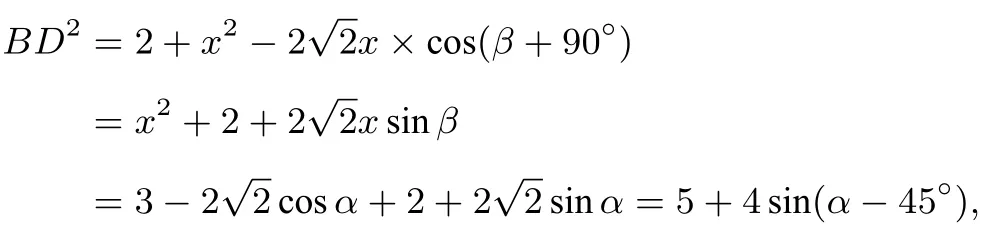
当且仅当α=135◦时,BD取得最大值为3.

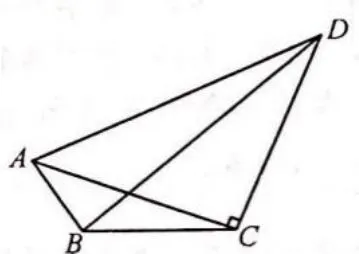
图4

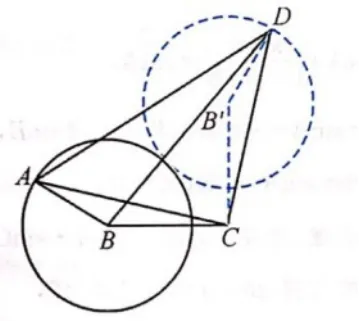
图5

解法2(几何视角)以B为圆心,固定BC,则点A在以B为圆心的单位圆上运动,注意到AC=CD,AC⊥CD,将∆ABC绕C点顺时针旋转90◦得到点D与点A重合,因此点D也在单位圆上运动,两圆外切,如图5,因此当且仅当两圆心共线时取得最大值为3r=3,其中r=AB=1.

解法3 (托勒密定理)由托勒密(Ptolemy)定理推论得AC·BD≤AB·CD+AD·BC,注意到即所以

题型二 面积最值问题

因此

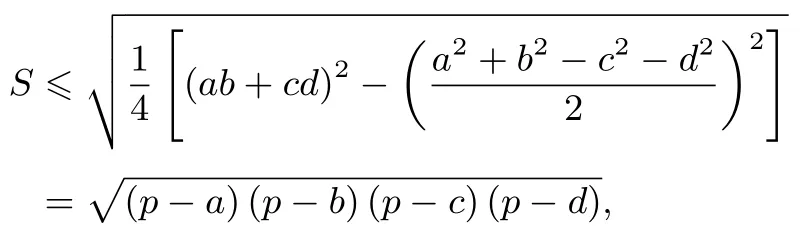
等号成立条件是B+D=π,即对角互补,四点共圆.

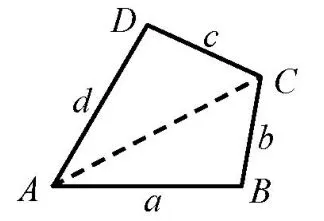
图6

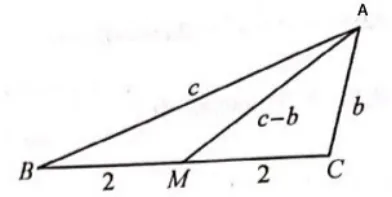
图7

例4如图7,在∆ABC中,角A,B,C所对的边分别是a,b,c,M是BC中点,BM=2,AM=c−b,当∆ABC面积的最大值为___.

总之,解决四边形边长或面积最值问题通常可以从代数的视角根据题意构建角或边长的目标函数再求最值,也可以从运动变化观点以几何的视角或解析的方法分析求解.