解三角形中求最值方法的探究

贵州省贵阳市花溪区溪南高中 杨昌举

在三角形中,求某些不确定量(式)的取值范围或最值,是高考中常见题型,归纳起来主要体现在:求角、边、周长、面积的范围或最值.这类题型知识能力的要求高、难度大,不仅要求学生要具备灵活运用正(余)弦定理的准确计算能力,而且更要求学生要有较强的观察、理解、分析与推理的思维演变能力.因此要解决此类问题,首先要充分掌握三角形中所存在的等量关系,比如,A+B+C=π,a=2RsinA,b=2RsinB,c=2RsinC(其中R为三角形的外接圆半径),c2=a2+b2−2abcosC;以及一些不等关系,比如,|a−b|＜c＜a+b,0＜A＜π,0＜A+B＜π,特别当∆ABC为锐角三角形时,a2+b2＞c2等;同时结合题设条件把所求问题进行合情推理、恒等变换(边化角,角化边),并从中寻找出引起不定量变化的参变量,再充分利用不等式相关性质、三角函数的有界性等,求出相关不定量(式)的最值或取值范围,进而厘清问题的本质.本文就对求角、边、周长、面积等的取值范围或最值的思维方法、分析方法和解决方法作简单的探究和归纳.

一、角的范围或最值

“角”是研究三角函数的核心,三角函数的取值范围与角的大小紧密关联,所以研究三角形中的“角”的取值范围或最值可借助三角函数的有界性,或利用正(余)弦定理把三角转换成边,再结合不等式的相关性质进行求解.

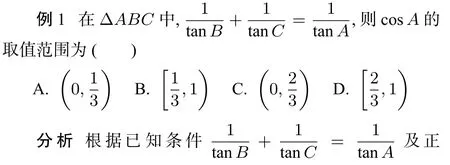
二、边的范围或最值

正(余)弦定理告诉了三角形中边与角相互转换的规律,这就凸显了正(余)弦定理的本质所在,因此研究和探讨边的取值范围或最值时,充分抓住边与角两元素的各自的特点,利用正(余)弦定理进行合理转换,问题就可以迎刃而解.

例2已知∆ABC的内角A,B,C的对边分别为a,b,c,且满足若a+b=2,则c的取值范围是____.

分析该题条件是边与角混合关系式,从结构上看,先用余弦定理进行恒等变换,可得等式为2cosC(acosB+bcosA)=c,再利用正弦定理得cosC=即所以由余弦定理得c2=a2+b2−2abcosC=(a+b)2−3ab,结合题设条件a+b=2和均值不等式可得ab≤1,当且仅当a=b=1时等号成立,所以c2≥1,即c≥1,又由三角形ABC中的不等关系知:c＜a+b=2,从而可得:1≤c＜2,即得c的取值范围是:[1,2).

三、周长的范围或最值

三角形周长问题可看作是边长问题的延伸,所以在解决周长相关问题时,可以类同求边长的取值范围和最值的方法进行求解,即利用正(余)弦定理把边转化成三角,或三角转化成边,把所求周长问题化为一元三角函数式或可利用均值不等式求出最值或取值范围.

例3∆ABC中,角A,B,C所对的边分别为a,b,c,且

(1)求角A的大小;

(2)若a=2,求∆ABC的周长的最大值.

四、面积的范围与最值

三角形的面积问题是边长与角问题的综合,解题中既要考虑边的变化,也要考虑相关角的变化,通常是利用面积公式,将其转化为同一类元素,然后利用三角函数的有界性或者实数的不等关系求解.

例4如图1,在平面四边形ABCD中,AD=2,CD=4,∆ABC为等边三角形,则三角形BCD面积的最大值是___.

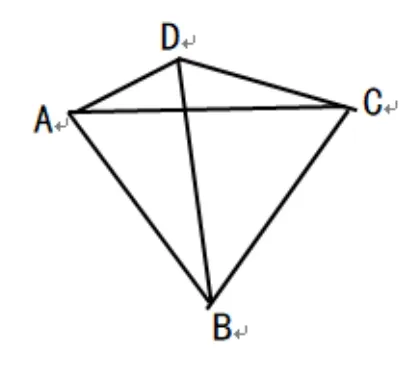
图1

分析由题设条件知:要求∆BCD的面积最大值,首先需结合已知条件寻求引起∆BCD面积变化的参变量.在三角形BCD中,CD为定值,结合图形和已知条件,易知,等边∆ABC边长的变化,则引起∠ADB的变化,从而∆BCD的面积就发生改变.

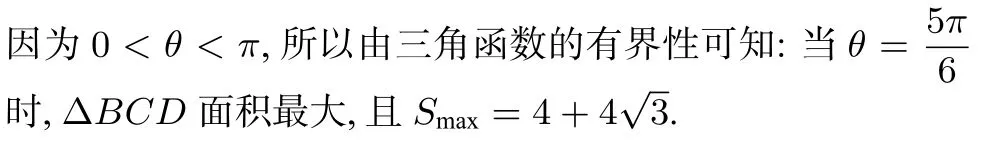
五、与其它知识点交汇的最值问题

研究三角形的对象主要是边、角和面积,其中边与角是研究问题的主体,且这些对象都是以实数大小体现出来,所以它们可以与其它知识点进行交汇,如向量、数列、不等式等等,解题时要综合运用这些知识和相关方法,灵活处理.

综上所述,我们不难发现:求三角形中不定量(式)的取值范围或最值,掌握正(余)弦定理的“本”(边化角,角化边)是解决问题的前提条件,能充分而又正确运用正(余)弦定理的“本”去实现三角形中边角关系的互换是解决问题所必须具备的能力,而问题能解决的关键是在正确运用正(余)弦定理的“本”的基础上合理运用不等式思想和三角函数思想,并通过利用不等式的性质(均值不等式等)和三角函数的有界性求出所求问题的结论.