不同湍流模型对后台阶流体流动的影响
刘 斐,陈方望
(1.中交第四公路工程局有限公司,北京 100022;2.武汉理工大学道路桥梁与结构工程湖北省重点实验室,武汉 430070)
日常生活中,大气与海洋的流动、高速管流、叶轮机械等绝大多数流体运动都属于湍流模型。湍流特性在工程中是常见的,因此也是研究学者高度重视的。湍流流动的核心特征是尺度无穷性和非线性,理论分析、实验研究抑或是计算机模拟来彻底认识湍流都是十分困难的。计算机的发展使得通过数值模拟对湍流的研究具有更高的操作性,更高精度的数值模拟是一直被需要的[1]。
在实际工程中,后台阶流动是一种非常经典的分离流动,其结构形式简单,但是能够近似模拟大多数实际工程中流体运动情况,如管道或河道突然变宽、风吹过障碍物等。国内外研究学者针对后台阶的流动已经做了不少理论和实验探究[2-5],肖潇[6]等人分析了后台阶流动的回流区特性和回流区长度变化规律;李通[7]等人分析了三维L型后台阶上半部分长高比值的差异对台阶表面流场特性的影响;王宇航[8]等人研究了三维后台阶模型在SA湍流模型、SST湍流模型和显示代数雷诺应力模型(EARSM)下的模拟结果,并对比实验结果发现EARSM的模拟结果更加接近实际情况;Lee等[9]对后台阶分离和再附流动的主要结构开展了试验探究,对大尺度涡结构的动力学特性进行了详细阐述;Otugen M V等[10]分析了再附位置对扩张比的影响,发现扩张比和再附点距台阶分离点的距离成正比关系。该文主要基于计算风工程几种常见的湍流模型,考虑后台阶中流体运动作为分析对象,以FLUENT为计算平台,对比分析了S-A模型、k-ε模型、RSM模型及LES模型等不同种湍流模型中模拟后台阶中的流体运动。
1 湍流模型分类
湍流模型是基于一定的约束条件对湍流流体流动的数学描述,其发展起来的种类很多,常用的湍流模型包括单方程S-A(Spalart-Allmaras)模型[11]、双方程k-ε模型、五方程雷诺力(RSM,Reynolds Stress Model)模型、大涡模拟(LES,Large Eddy Simulation)模型[12,13]等,以下对各个湍流模型原理做详细介绍。
1.1 S-A模型
湍流时均的连续性方程与雷诺方程如下
(1)
(2)
(3)
式中,ρ为流体密度,kg/m3;u为流速,m/s;μ为流体动力黏度,Pa·s;φT为流体参数;S为源项。
单方程S-A模型是在湍流时均的连续性方程与雷诺方程的基础之上,再建立了一个湍动能k的运输方程,将湍流黏度μt表示成k的函数,从而使方程组封闭。湍动能k的运输方程为
(4)
式中,σk、CD、Cμ为经验常数,σk=1,CD=0.09,Cμ=0.08~0.38。
(5)
1.2 k-ε模型
1)标准k-ε模型
在湍动能k方程的基础上,引入了一个湍动耗散率ε的方程,形成k-ε双方程模型,称为标准k-ε模型。该模型由Launder和Spalding于1972年提出。模型中的ε定义为
(6)
于是,湍动黏度μt可表示为k与ε的函数
(7)
因此,标准k-ε模型的运输方程为
(8)
(9)
其中
(10)
式中,C1ε、C2ε、C3ε为经验常数,默认值为C1ε=1.44、C2ε=1.90、C3ε=0.09;σk、σε分别为湍动能和湍动耗散率对应的普朗特数,默认值为σk=1.0、σε=1.3;Prt为湍动普朗特数,默认值取Prt=0.85;gi为重力加速度在i方向上的分量;β为热膨胀系数;Mt为湍动马赫数;a为声速。
2)重整化k-ε模型
重整化k-ε模型(RNGk-ε模型)是由Yakhot和Orzag提出的,它是对瞬时N-S方程用重整化的数学方法推导出来的模型。模型中的常数与标准k-ε模型不同,而且方程中也出现了新的函数或项。所得到的湍动能和耗散率方程与标准k-ε模型相似,为
(11)
(12)
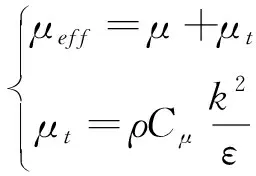
(13)
3)可实现k-ε模型
标准k-ε模型对时均应变率有特别大的情性,有可能导致负的正应力。为使流动符合湍流的物理定律,需要对正应力进行某种数学约束。可实现k-ε模型正是基于此提出,其湍动能及耗散率输运方程为
(14)
(15)
(16)
式中,C1ε、C2ε、C3ε、C2、A0为经验常数,默认值为C1ε=1.44、C2ε=1.92、C3ε=0.09、C2=1.9、A0=4.0;σk,σε分别为湍动能和湍动耗散率对应的普朗特数,默认值为σk=1.0σε=1.3。
1.3 RSM模型
上述介绍的各种双方程模型都采用各向同性的湍流黏度来计算湍流应力,这些模型很难模拟出旋转流动及流动方向表面曲率变化的影响。为克服这些缺点,有必要直接对雷诺方程中的湍流脉动应力建立微分方程式并进行求解。
雷诺应力模型就是求解雷诺应力张量的各个分量的输运方程,具体形式为
(17)
(18)
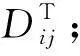
1.4 LES模型
大涡模型的控制方程是对N-S方程在波数空间或物理空间进行过滤得到的。过滤的过程是去掉比过滤宽度或给定物理宽度小的涡旋,从而得到大涡旋的控制方程为
(19)
(20)
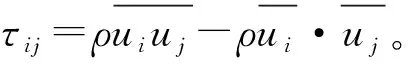
2 不同湍流模型的对比计算与分析
模拟在后台阶装置中流体流动的现象。如图1为几何模型尺寸图,其中模型左侧设置为速度进口,尺寸为0.1 m,水流以0.2 m/s流入;右侧为自由出口,尺寸为0.2 m;上侧为对称边界,尺寸为2 m;下侧为壁面边界,为台阶状,高度为0.1 m,上下台阶长度均为1 m。
依据所述的后台阶装置的相关参数在ANSYS自带ICEM CFD建立有限元模型如图2所示,单元总数为12 730,节点个数为12 251,单元尺寸为0.005 m。对模型采用不同的湍流模型进行计算,包括k-epsilon(2eqn)标准模型、k-epsilon(2eqn)重整化模型、k-epsilon(2eqn)可实现模型、k-omega(2eqn)标准模型、k-omega(2eqn)BSL模型、k-omega(2eqn)SST模型等,计算结果如图3~8所示,包括压力云图和速度云图。





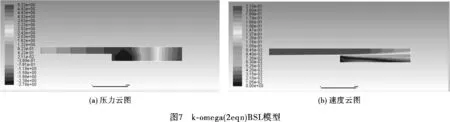
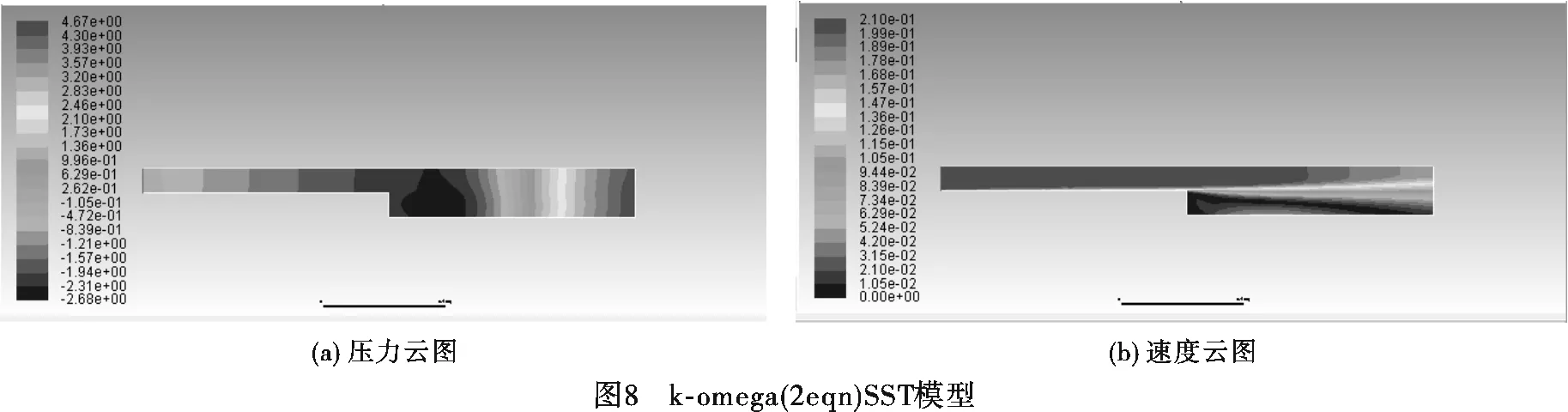
比较分析图3~图8可以发现:
1)流体在截面小的区域流动时速度要比在截面大的区域流动时大得多,且在截面变化处会存在速度趋近于零的流体,在流体出口处,流体速度并不会均匀或接近均匀流出,而是出现了很明显的分层,上部速度最大,底层速度趋近于零。
2)流体在流动过程中与壁面接触的流体速度会小于没有与壁面接触的流体速度。
3)在截面发生突变的位置,流体压力会急剧降低称为负值,且入口处的压力小于出口处的压力。
4)湍流模型选取的不同,对计算的结果有一定的影响;其中不同湍流模型得到的压力云图在总体分布上有较大差异,且最大值相差也很明显,k-epsilon(2eqn)的三种模型在压力云图最大值的差别上要小于k-omega(2eqn)的三种模型计算得到的压力云图最大值之间的差异。
5)不同种模型计算得到的速度云图在速度分布上差异不是很明显,且速度最大值也相差不大,但还是有微量的差异。
3 结 语
针对已有学者提出的不同种湍流模型,对比分析了不同种湍流模型在同一个后台阶装置中应用时,后台阶内部流体流动的情况,包括压力云图和速度云图。结果表明:湍流模型选取的不同,对计算的结果有一定的影响;其中不同湍流模型得到的压力云图在总体分布上有较大差异,且最大值相差也很明显,k-epsilon(2eqn)的三种模型在压力云图最大值的差别上要小于k-omega(2eqn)的三种模型计算得到的压力云图最大值之间的差异;不同种湍流模型计算得到的速度云图在速度分布上差异不是很明显,且速度最大值也相差不大,仅存在有微量的差异。

