基于理想点法模型的辽阳县农田水利基础设施评价

李 鹏

(辽阳县水利事务服务中心刘二堡站， 辽宁 辽阳 111200)

0 引 言

我国农业生产力布局与降雨时空变异、水资源时空分布等呈现出明显的不协调性特征，农田水利设施为促进我国经济发展的关键和现代农业发展的重要保障，做好农田水利工程建设工作对改善人们生活水平、促进当地粮食增产、推进农业产业化经营及增强区域农业抗旱能力等具有重要作用。21世纪以来，随着经济的发展、人口数量的显著增大、城镇化及工业化的加快，特别是生活城市化、农业和非农业产业的快速发展加剧了人类活动与生态环境、农业产业、城镇竞争用水之间的矛盾，农田水利不仅要解决水质性、管理性、水源性及工程性缺水问题，而且还要满足传统的防洪抗旱、灌溉排水等要求。然而，由于农田水利存在建设标准低、运行机制和管理实施不完善等问题，严重制约着农田水利的可持续运行和工程效应的发挥，所以有必要研究探索农田水利的建设与管理综合水平[1-5]。

辽阳县农田水利建设与管理的快速发展，使得在实际推进过程中面临着一系列的挑战。根据实地考察与查阅有关资料，辽阳县出台了促进农田水利建设与管理机制，明确提出了要促进建设与管理工作的持续有效进行。经过多年的努力和发展，当地农田水利的灌溉排水并未取得的明显成效，水利设施的年年建设并没有增大能够良好运转的工程数量，也并没有减少有人用无人管的现象，部分年份和局部地区的灌溉水保证率与有效利用系数虽然得到一定的提升，但仍保持在0.45-0.50的较低水平；许多基础设施存在后续维护保障能力不足、建设质量标准低、建设规模小和相关配套设施差等问题。所以，辽阳县当前的农田水利仍难以满足工程实践、农业生产的要求[6-9]。鉴于此，本文从水质自净、降泽、抗旱、排涝和防洪等方面综合评价了当地农田水利设施的状态。

1 基于理想点法的评价模型

1.1 TOPSIS模型简介

TOPSIS模型又称为多指标、多目标决策分析法，其本质是依据理想化目标与有限个评价对象间的贴近程度，科学排序相关指标的功能作用或优劣程度，具有应用灵活、计算结果科学和分析简便等优点。所以，在农田水利设施评价中该模型的应用较为广泛，在实践应用中其评价原理如下：

1) 通过检测最劣解、最优解与待评价对象之间距离，单调排序评价对象的目标变量整体状况。

2) 科学评价评价目标变量的优、劣程度，最优结果为距离最劣解最远且离最优解最近的对象；反之，则为绩效评价的最劣解，即评价结果距离最优解最远且距离最劣解最近。

3) 各评价指标的最优、最劣值即为最优和最劣评价结果。

1.2 模型构建流程

步骤一：建立决策矩阵。根据相关文献中TOPSIS模型计算流程和建模步骤，引入M=(M1,M2,…,Mm)、C=(C1,C2,…,Cm)分别为TOPSIS模型的多指标决策集和多指标集，关于指标Ci=(C1,C2,…,Ci)决策方案M=(M1,M2,…,Mm)的参数值为Xij，其中i=1,2…,n；j=i=1,2…,m。从而构建多目标决策矩阵如下：

(1)

步骤二：无量纲化处理决策矩阵。由于各参评指标的量纲存在差异无法直接用于最终决策的计算，为提高数据的平滑度必须对各维因子值进行无量纲化处理。本文采用下述公式进行处理，其表达式为：

(2)

步骤三：构建加权决策矩阵。TOPSIS模型的加权决策矩阵根据各指标权重W和无量化处理后的矩阵计算，即：

Z=(rij)m×n

(3)

步骤四：熵权法确定权重。信息熵反映了TOPSIS模型中样本数据的相对变化速率，所以信息熵的大小代表了指标信息在系统中的无序程度，利用该理论计算指标权重。采用熵权法确定指标权重的主要依据为各参数构成的判断矩阵，信息量越大则该参数提供的有效信息越大，在评价过程中其重要性程度越高，赋予的权值就越大；反之，信息量越低则样本提供的信息越少，在评价过程中该样本的重要程度越低，确定的权值就越小。对各指标权重利用熵值法计算时应尽可能的降低主观性影响，从而提高评价结果的准确性和合理性。其计算公式如下：

(4)

式中：H、n为评价指标熵和参评指标数量；Wj为各指标权重。

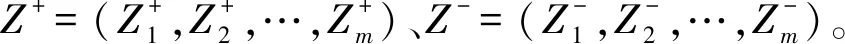
步骤六：计算欧式距离。对最优解与各评价对象之间的距离进行求解，选用欧式基本公式对最优、最劣方案进行欧式距离计算，计算公式如下：

(5)

步骤七：贴进度Ci的计算。依据待评价对象的贴近程度值Ci的大小对农田水利设施进行优劣排序，Ci值越大则表示决策样本方案与最优方案的贴近程度越高，水利设施的保障能力越强；反之，则表示与最优方案的贴近程度越低，水利设施的保障能力越差，计算方法为：

(6)

2 农田水利基础设施评价

2.1 灌区概况

辽阳县境内的小型灌区大多建设于1950-1960年，灌区内主干工程经多年的服役运行，主要存在灌溉方式粗放、渠系分布不合理、大部分骨干建筑物老化失修、灌溉技术落后、输水损失大等问题，水利设施完好率不足60%，严重阻碍了农业经济的可持续发展和灌区灌溉的正常运行，对当地农村经济发展和农业生产构成严重的威胁。由于过流量的减少使得灌溉渗流量较大，灌溉历时较长导致农业灌溉效率地下，不仅增加了农民的农田灌溉和水利管理难度，而且严重影响着灌区的正常运行。另外，虽然灌区内具有较为丰富的水资源量，为进一步提升灌溉保证率和用水效率必须推广高新节水灌溉、渠系防渗、灌溉输水等续建配套节水改造工程。

为适应新阶段的农村经济发展要求，进一步提升优质水稻的总体生产水平，推动农业节水灌溉技术的普及与深入发展，辽阳县相关部门将亟待解决改造的末级渠系以及在灌区发挥关键作用的项目列入改造范围，重点对灌区配套不全的斗、农渠闸涵进行更新改造。因此，本文从水质自净、降泽、抗旱、排涝和防洪等方面综合评价了当地5个小型灌区的农田水利设施的运行状态。

2.2 评价流程

根据以上TOPSIS模型基本流程计算方法，科学评价辽阳县5个小型灌区的水利设施。运用信息熵理论计算确定水质净化、降泽、抗旱、排涝、防洪指标权重，并结合专家意见和相关文献资料综合评价了各灌区的水利设施保障能力，如表1所示。

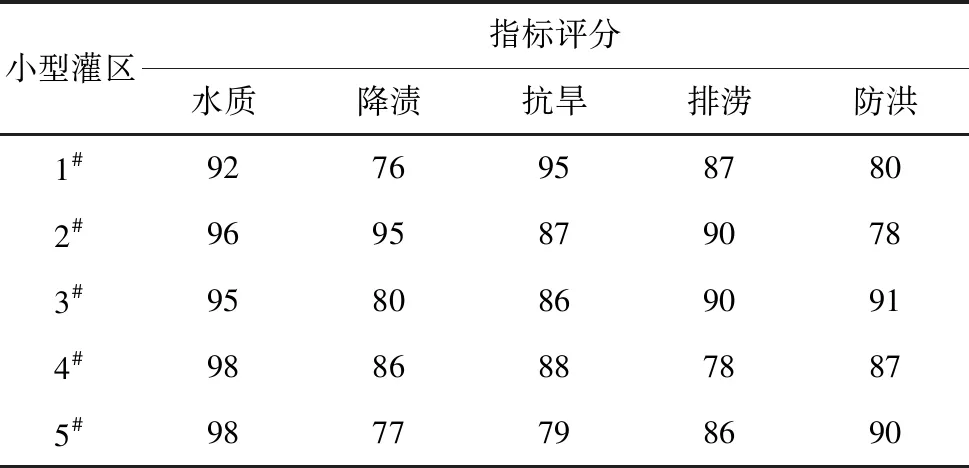
表1 基于专家评分法的农田水利设施评分

对辽阳县农田水利设施综合保障能力采用TOPSIS模型和以上数据指标进行评价，主要流程如下：

1) 构造决策矩阵。各评价指标的初始数值因存在较大差异，因此需采用无量纲化公式对各参数值作统一处理，从而得到标准数列，如表2所示。

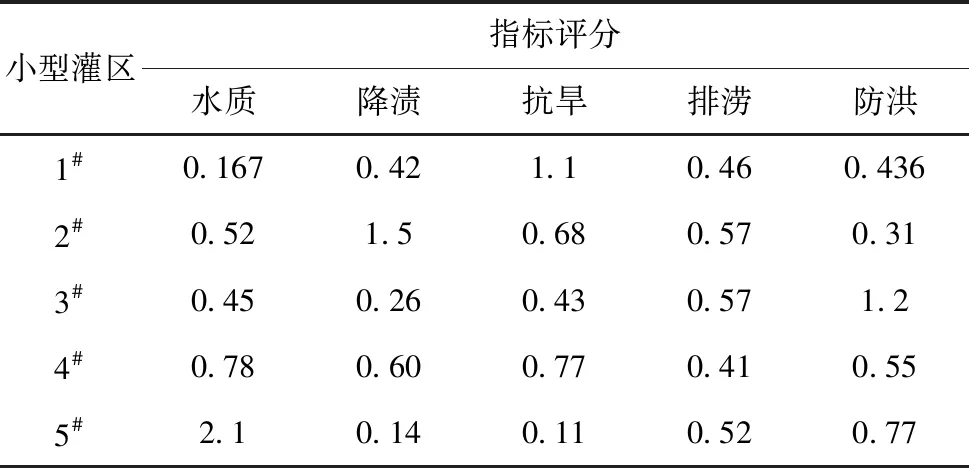
表2 农田水利各评价指标标准值

3) 根据最劣和最优向量的具体内涵，按照各评价指标数值构造向量如下：

最优向量：Z+=(0.231,0.155,0.158,0.242,0.231)；

最劣向量：Z-=(0,0,0,0,0)。

4) 计算欧式距离。对最优解与各评价对象之间的距离进行求解，选用文中所述公式对最优、最劣方案进行欧式距离计算，结果如下：

最优距离：D+=(0.220,0.218,0.192,0.180,0.224；)

最劣距离：D-=(0.161,0.192,0.180,0.155,0.174)。

5) 计算贴进度Ci。根据贴近程度值Ci的大小对农田水利设施进行优劣排序，Ci值越大则表示水利设施的保障能力越强；反之，则表示与最优方案的贴近程度越低，水利设施的保障能力越差，其结果如下：

C=(0.510,0.522,0.615,0.601,0.613)

6) 最终排序。综合考虑水质、降渍、抗旱、排涝和防洪能力等指标，对辽阳县5个小型灌区水利设施进行综合排序，结果如表3所示。

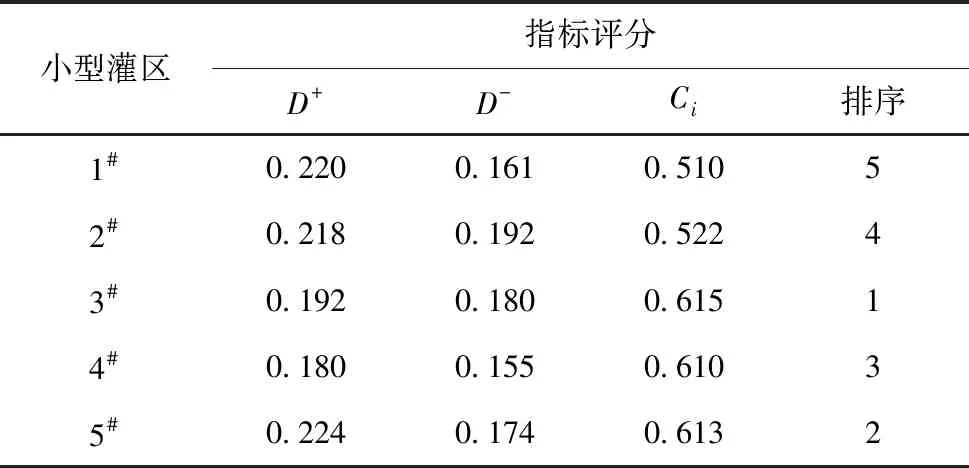
表3 农田水利设施评价结果

根据表3可知，在水质净化、降渍、抗旱、排涝、防洪等方面综合保障能力较强的农田水利设施位于3#灌区，其最优贴近程度为61.5%；其他4个灌区的综合保障能力相对较弱，按由大到小的次序排列为5#、4#、2#、1#灌区，所对应的最优贴进度分别为61.3%、61.0%、52.2%、51.0%。因此，辽阳县5个小型灌区的水利设施综合评价结果分别为3#>5#>4#>2#>1#。

研究表明，不同农田水利的建设状况在辽阳县各地区存在较大差异，这主要与灌区水利施工技术、建设资金等因素相关。农田水利建设的评价过程复杂、涉及到的影响因素较多，综合考虑各方面因素客观、合理的评价水利建设状况，对于促进灌区持续发展具有重要作用。管理情况和水利设施运行状况为制约农业水利设施持续健康运行的关键因素，若能够加大续建配套和田间节水改造力度，最大限度的提升灌区水利用系数和灌溉面积，将显著提升水利设施效益评价各参数值和综合评价值。

3 结 论

在处理多因素、多目标综合复杂问题时TOPSIS模型具有较强的实用性与科学性，运用TOPSIS模型对辽阳县5个灌区的农田水利设施进行评价。结果显示，在水质净化、降渍、抗旱、排涝、防洪等方面不同罐区的水利设施保障能力存在较大差异。因此，应结合不同地区的水利特征、分布特点加强建设与管理。近年来，辽阳县开展了一系列的节水灌溉、引提水工程，在显著增大工程装机量和农业灌溉能力的同时，大大提高了灌区的防洪能力和有效灌溉面积，从本质上改善了当地农业发展环境和生产技术水平，为增加农民收入和促进当地发展提供了重要的基础。