基于链路重构策略的网络抗毁性优化研究

史文博，刘 东，杨博文

(国防科技大学 信息通信学院，湖北 武汉 430014)

0 引 言

随着科学技术的不断发展，通过对现有网络进行重构，可以达到显著提高网络抗毁性性能的目的，对提升通信网络抗打击能力具有十分重要的意义。

祁兵等人[1]采用建立环路保护的思想来提高电力通信网络的抗毁性能。冯颜[2]则主要考虑了通信网络在受到打击破坏后的动态修复。张赛男、刘东亮[3]利用CW节约算法以及遗传算法实现网络优化，该方法结合了CW节约算法快速收敛以及遗传算法避免局部最优解的特性，并将该方法与贪婪算法的网络优化结果进行实验对比。彭观胜[4]提出基于禁忌搜索的复杂网络抗毁性优化算法。宋晓峰等人[5]用克隆选择算法对网络的抗毁性进行优化。Wang Wei[6]研究基于随机游走间度(RB)的级联故障模型,实现了复杂网络的级联故障预防。

文中主要对无线通信网络实现抗毁性优化。首先分析了网络抗毁性与聚合度的内在联系；其次对传统HBF-α算法链路重构策略进行调整，提高了网络优化效果；然后结合通信网络实际要求，提出了保证节点度不变的链路重构策略，使用模拟退火算法有效解决了HBF-α策略中局部最优解问题，并分析对比两种优化方案的适用情形、优化程度以及时间开销；最后总结全文，并提出下一步的研究重点。

1 网络抗毁性分析

在通信网络打击过程中，关键节点[7]常常是优先打击目标。根据田秀雯在文献[8]中对网络聚合度与定点打击下网络崩溃的临界值之间关系的分析，发现降低该临界值与降低网络聚合度对网络抗毁性能提升基本一致。下面以由12个通信节点与27条链路组成的通信网络为例，随机移除链路，同时随机建立链路，保持总节点数目与链路数量不变。不同网络结构下的聚合度与抗毁性[9]指标值关系如图1所示。

图1 网络抗毁性与聚合度关系

可以看出，网络抗毁性与网络聚合度呈反比例关系。故可以通过降低网络聚合度[10]、实现节点重要度[11]均衡的方式优化网络抗毁性能。

对于链路可以重构的无线通信网络，常采用移除关键节点间链路[12]的方法来有效提升网络抗毁性能，同时，降低网络聚合度也可以避免部分节点因负载较大而崩溃的情况发生，但网络的经济开销将会增加[13]。在移除了部分链路之后，从均衡的角度出发，在业务量较小的节点之间建立新的链路，实现网络流量再均衡，网络抗毁性可以得到优化。

2 HBF-α算法优化及实验分析

2.1 算法步骤

HBF-α策略：对通信网络中所有链路赋值，权重Aij由该链路两端的节点的重要度值之和决定，Aij=G(vi)+G(vj)，赋值结果为A1,A2,…,An，寻找到其中最大的权值，该权值对应的链路即为需要移除的链路。在移除掉该链路后，随机在所有的节点中选取两个节点，当两节点间不存在链路时，建立新的链路，否则重新随机选取节点对。重复上述操作直到达到规定的抗毁性指标要求，理论上该方法可以将网络聚合度降到趋近于0[14]。

对HBF-α算法的新建链路策略进行优化，算法步骤如下：

(1)对所有链路进行赋值并记为该链路的权重，权重Aij由该链路两端的节点的重要度值之和决定，即Aij=G(vi)+G(vj)，并依据链路的权值大小顺序从大到小记为A1,A2,…,An。

(2)按照A1,A2,…,An的顺序依次移除链路，当移除链路会造成节点中断时，保留该条链路，当移除链路的比例达到规定的重构比例时，停止移除。

(3)计算第二步中移除规定比例链路后的节点重要度，在节点重要度之和最小的两节点之间建立新的链路，当链路已经存在时，选择重要度之和次小的节点，以此类推。

(4)循环进行上述(3)操作，直至通信网络的链路总数量达到原网络的链路数量时停止。

2.2 实验分析

以0.2的连通概率随机生成一个20*20的无向网络结构，该网络共有98条链路，节点容量均为20，网络拓扑图如图2所示。

图2 20*20网络拓扑

使用HBF-α策略和改进后的算法分别对该20*20的通信网络进行优化。两种链路重构策略不同重构比例下的网络聚合度(与网络抗毁性呈反比)变化规律如图3所示。

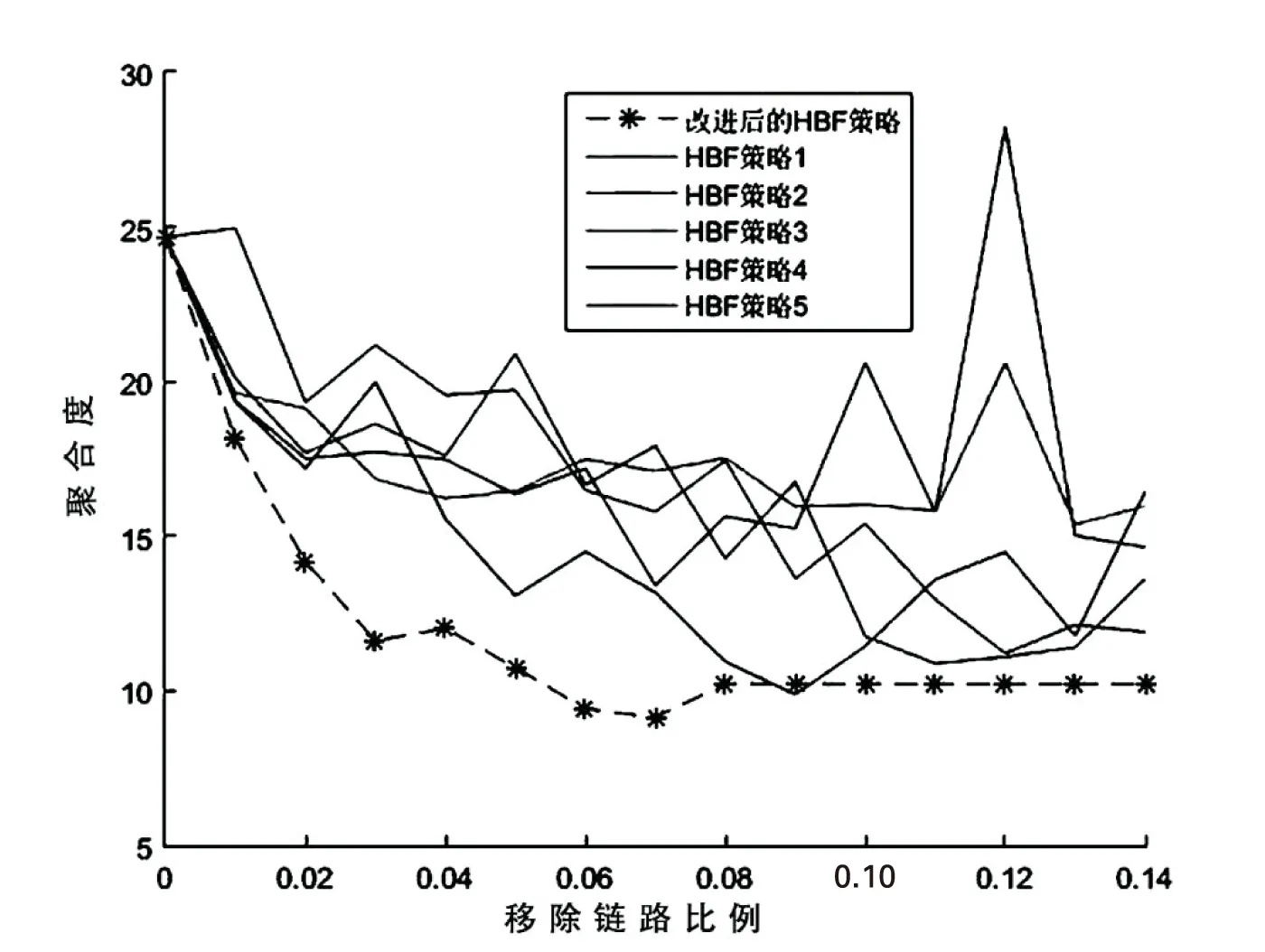
图3 聚合度变化

可以看出，当网络规模较大时，改进后的算法网络抗毁性优化能力高于HBF-α策略，当重构比例大于0.04后，网络抗毁性优化效果下降，在对0.06比例的链路进行重构优化后，网络抗毁性大约提高了2.13倍，网络链路数量保持不变，满足优化要求。对于规模较小的网络结构，以12*12的通信网络为例，两种链路重构策略不同重构比例下的网络聚合度变化规律如图4所示。

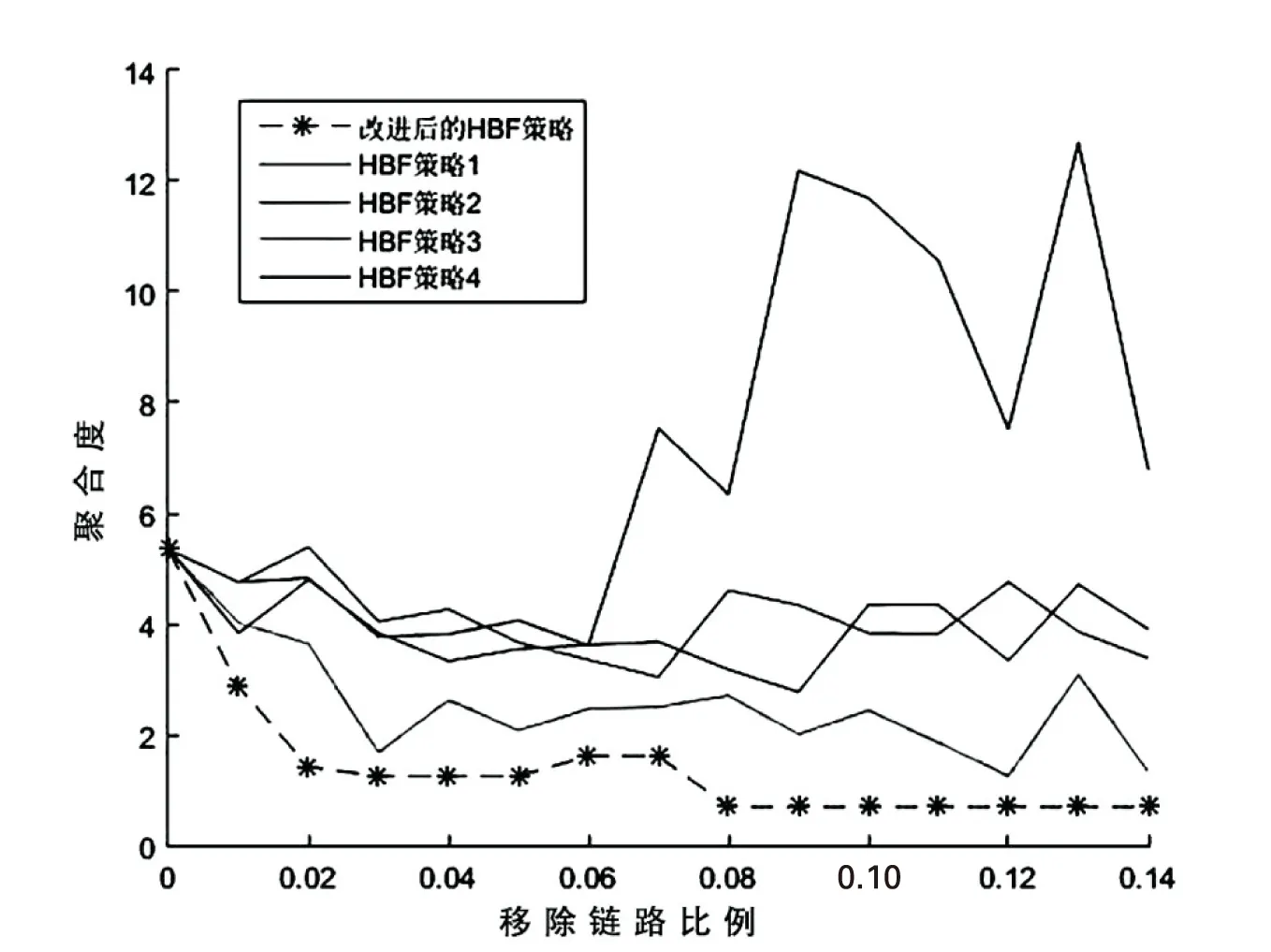
图4 12*12网络聚合度变化

可以看出，改进后的算法优化效果稳定、适应性较强、收敛速度快，网络容量以及网络通信能力都得到了一定的提升，但存在优化瓶颈，当达到一定的优化程度后网络趋于稳定，无法对网络进行进一步的优化，而HBF-α算法容错率较低，尤其是当网络规模较小时，优化稳定性差，在几次优化过程中，对网络的优化程度各不相同，这是其新建链路的随机性而决定的。

改进后的HBF-α算法对网络抗毁性实现优化是在重新调整网络节点度的基础上进行的，适用于重构灵活且对节点可同时建链的数量不做要求的通信网络。

3 基于模拟退火算法的网络抗毁性优化

在实际通信网络中，不同节点的层级以及功能不同，其节点度在优化过程中应当基本保持不变，例如作为末端节点，其节点度应当保持为1，作为级别较高的上一级通信节点，其度应当在3左右。故对HBF-α的重构策略进行调整，以符合通信网络重构过程中任意节点建立链路总数不变的要求，即节点度保持不变。采用模拟退火算法[15]解决HBF-α算法中的优化瓶颈问题，提出了基于模拟退火算法的网络抗毁性优化方法。

调整后的重构策略如下所述，用于生成新的通信网络：

(1)随机选择网络中的任意两个节点va,vb，并建立点集Va,Vb(分别为节点va,vb的邻接节点集合)。

(2)随机选择点集Va中任意节点vaj。该节点不能为节点vb、点集Vb中的元素。同时随机选择点集Vb中任意一个节点vbj，同理，该节点不能是节点va、点集Va中的元素。

(3)移除链路va→vaj与链路vb→vbj，并建立va→vbj与vb→vaj两条新的链路，完成对网络的重构，判断新的网络是否为全连通网络，如果符合条件，完成重构步骤，否则返回第一步重新选择节点，依次进行上述操作。

目标函数为通信网络聚合度J(D)：

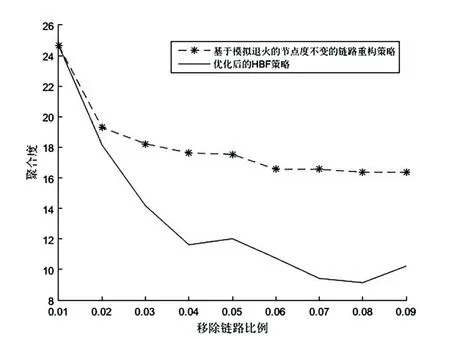
图5 抗毁性优化过程对比

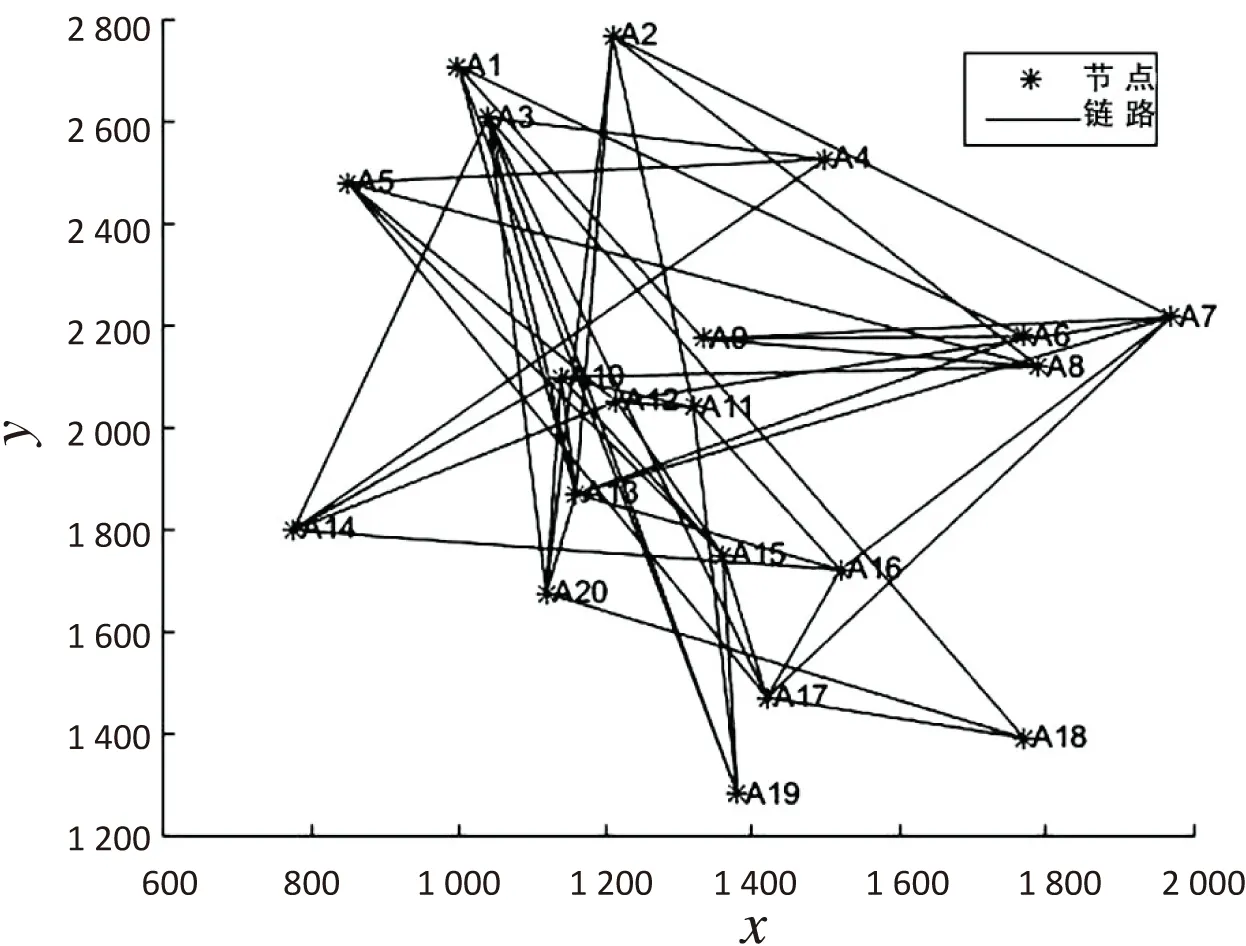
图6 优化重建策略的HBF-α算法

可以看出，基于模拟退火的网络抗毁性优化方法优化效果稳定，可以有效避免局部最优解，但与调整了链路重构策略后的HBF-α算法的优化结果相比较，最终网络抗毁性优化效果相对较差，这是其保持节点度不变的链路重构策略所决定的。优化后的网络的节点度标准差如表1所示。

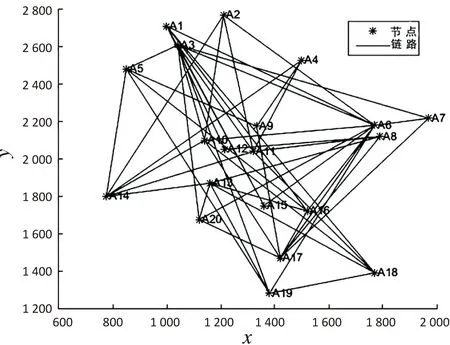
图7 基于模拟退火的网络抗毁性优化方法

表1 网络节点度标准差对比

一般来说，节点度越大，与该节点相连接的链路数量越多，与此同时，该节点重要度就会偏大，导致网络聚合度偏大，在HBF-α算法的优化结果中可以看到优化后网络的节点度标准差降低。而模拟退火优化算法的节点度标准差未发生变化，虽然优化的最终效果相对较差，但符合通信网络重构过程中任意节点建立链路总数不变的要求。重构6%链路时两种策略的时间开销如表2所示。

表2 时间开销对比

可见，基于模拟退火的网络抗毁性优化算法虽然优化效果较好，但产生的时间花销极大，因此在网络抗毁性优化应用中，该方法适合于规模较小、对节点建链数量有着相关限制的网络，例如军事通信网。而优化的HBF-α策略适合于较大规模的通信网络，且对网络中各个节点的建链能力有着较高的要求。根据不同的通信背景，采取合理的链路重构策略，可以有效实现通信网络抗毁性优化。

4 结束语

针对网络抗毁性优化问题，优化重构策略后的HBF-α算法复杂度低、收敛速度快、效率较高，但存在优化程度有限、适用范围较小等问题。对于基于模拟退火的网络优化方法，在调整了链路重构策略后，优化结果更加贴近实际需求，但算法复杂度高。由于模拟退火算法中目标函数的计算是基于最短路径求解的，进一步加剧了计算的复杂度，因此下一步可以通过寻求其他计算复杂度较低的有效指标更换目标函数，提高算法效率。