分片响应面法在随机振动响应分析中的应用
朱思宇 李永乐 向天宇

摘要:在分析结构的随机振动响应时,响应面法(Response Surface Method)可有效地降低随机仿真的计算代价。然而,当随机变量存在大变异系数时,传统的响应面法无法满足所要求的精度。分片响应面基于对随机变量变异系数进行合理分块的原则,缩小响应面的近似范围,并对分割后的响应面进行独立分析,从而提高了响应面在该空间的近似精度。首先采用分块响应面法结合蒙特卡洛MC抽样技术,以单质点振子模型的随机振动响应为算例,对分块响应面法的正确性进行验证。计算结果表明,在随机变量的变异系数不大时,分片响应面法的计算精度不低于传统响应面法,而当随机变量具有大变异系数时,分片响应面法的近似精度远高于传统响应面法。此外,以随机地震动作用下的桥墩随机振动为背景,将该方法进行了进一步地推广及应用。
关键词:随机振动;响应面法;蒙特卡洛方法;分片响应面法;变异系数
中图分类号:0324;P315.9 文献标志码:A 文章编号:1004-4523(2020)01-0105-06
DOI:10.16385/j.cnki.issn.1004-4523.2020.01.012
引言
对于经典随机振动分析理论来说,往往采用结构响应的方差值作为响应结果统计量的目标值进行求解。然而,当不确定性参数参与随机振动计算中时,经典的随机振动理论将不再适用于求解工作,仅仅得到结构响应的方差结果也不再能够满足计算要求。针对大型复杂结构的随机振动问题,蒙特卡洛(Mc)方法存在着计算耗能过大的缺点,无法适用于求解工作。
响应面法是一种常用的近似技术,它通过对函数的一系列已知点进行拟合从而推测函数的变化趋势。Faravelli以最小二乘法来估算响应面的系数建立了以实验设计为基础的响应面法;Das等对响应面含交叉二次项的二次多项式展开讨论,通过保留对可靠度计算影响较大的交叉项改进的响应面法,与不含交叉项的二次多项式进行相比,其计算精度有所提高;Gupta等提出改进的响应面函数,当某些变量贡献比较小时用一常数代替变量值,进行模型转换。Der Kiureghian等提出了基于概率配点法的随机响应面方法,并首次运用于环境和生物系统的不确定性分析。在国外,响应面法已在结构可靠度分析领域得到了广泛的应用。
近年来,响应面的改进方法取得了长足的进步,均能够有效地提高其计算的精度和效率。但是,随机变量存在大变异系数情况下,响应面模拟精度问题的相关研究较少。本文对传统响应面法进行改进,并提出了分片响应面法,旨在解决大变异系数随机变量的模拟精度问题,并提供一定的数据支持。运用所提出方法,以单质点振子在高斯白噪声激励作用下的随机振动响应为例,与直接MC抽样结果进行对比,验证了分片响应面法的正确性。此外,将分片响应面法结合MC抽样技术运用于随机地震激励作用下的桥墩结构的随机振动响应分析。
1理论方法
1.1不确定性虚拟激励算法
响应面拟合过程中的样本分析采用了不确定性虚拟激励法,该方法以虚拟激励算法的核心思想为基础,将所模拟的虚拟激励转变为具有随机特性的输入激励(称之为不确定性虚拟激励),有别于确定性结构的随机振动响应分析过程。本文以多自由
2单质点振子随机振动响应分析
本文首先采用平稳白噪声激励下的单自由度振子随机振动响应进行验证。其线性振子运动方程可表示为
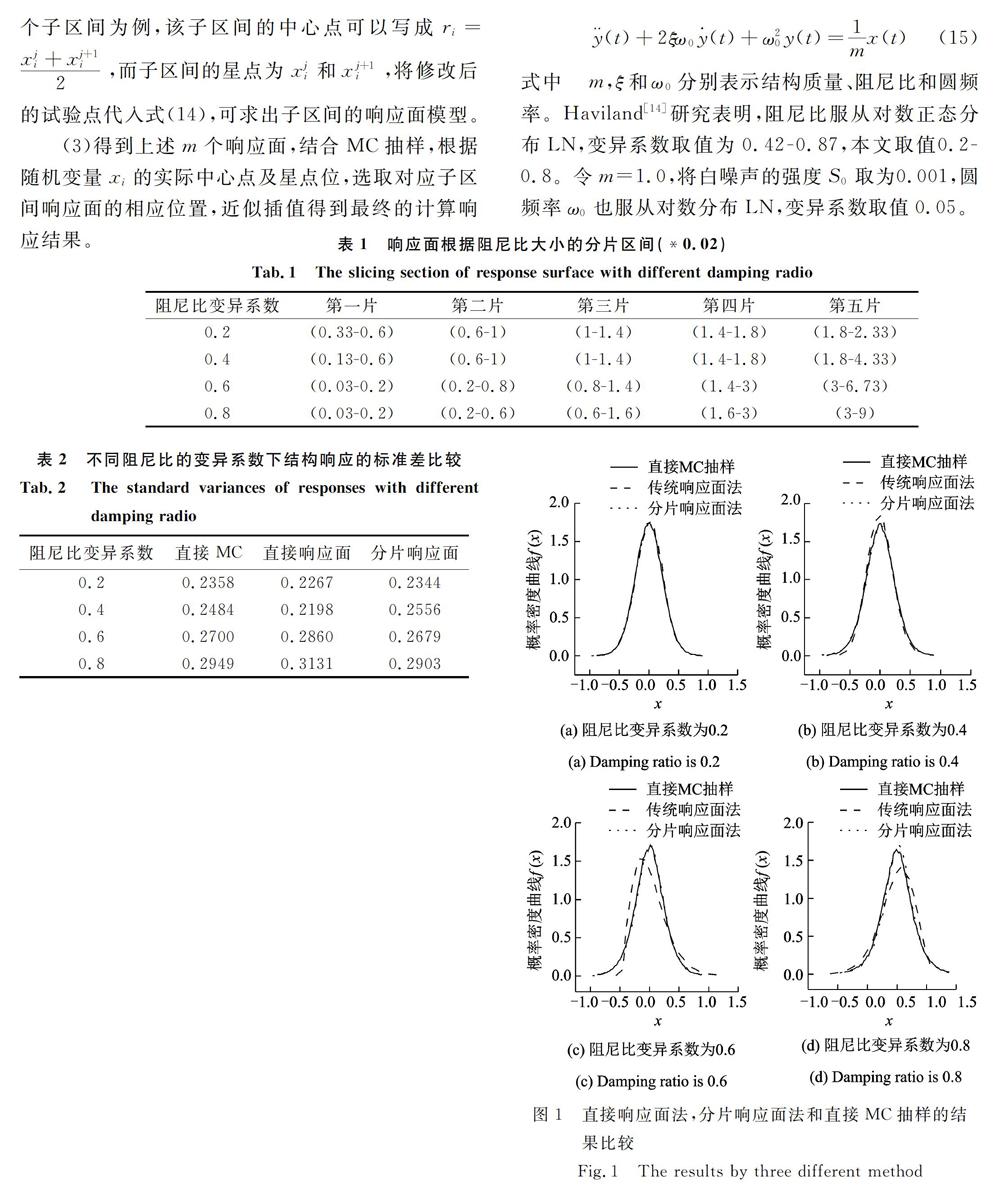
分析结构的随机振动时,考虑功率谱密度函数的对称性,按单边谱计算。由于圆频率随机性对结构响应方差影响相对于阻尼比随机性来说较小,本文选取圆频率均值1.0,圆频率变异系数0.05,阻尼比均值0.03,阻尼比变异系数0.2-0.8进行响应面拟合。根据阻尼比变异系数,绘制得到了相应的概率密度曲线,并对其进行分片处理,如表1所示。基于所划分的概率密度函数子区问,带人式(15)进行求解后并整合得到最终结果。不同阻尼比变异系数下的直接响应面法和分片响应面法计算的结构响应的标准差与直接MC抽样计算结果比较如表2所示,概率密度曲线拟合如图1所示。
从表2分析得出,当阻尼比变异系数小于0.4的时候,采用直接响应面法求解所得结果满足工程精度要求,但当阻尼比逐渐增大,直接响应面法所得结果与MC抽样结果的匹配度不断降低,无法满足工程精度要求。但是,无论阻尼比变异系数如何变化,分片响应面法运算结果均能满足精度要求。
从图1可以看出,当阻尼比变异系数较小时,直接响应面法计算的概率密度曲线结果与直接MC抽样可以较好地吻合,当阻尼比变异系数取0.4时已经出现吻合偏差,随着阻尼比变异系数逐渐增大,直接利用响应面拟合结构的响应误差也越来越大。当阻尼比变异系数取0.6-0.8时,已经明显不满足工程精度。本文提出对阻尼比大的变异系数取值进行区问划分重新拟合响应面的方法可以较好地解决该问题。经过对阻尼比进行区问划分(本文划分成5个区问)之后,再进行响应面拟合,可以较好地与直接MC抽样吻合。
3桥墩结构在地震作用下随机振动响应分析
3.1桥墩工程背景介绍
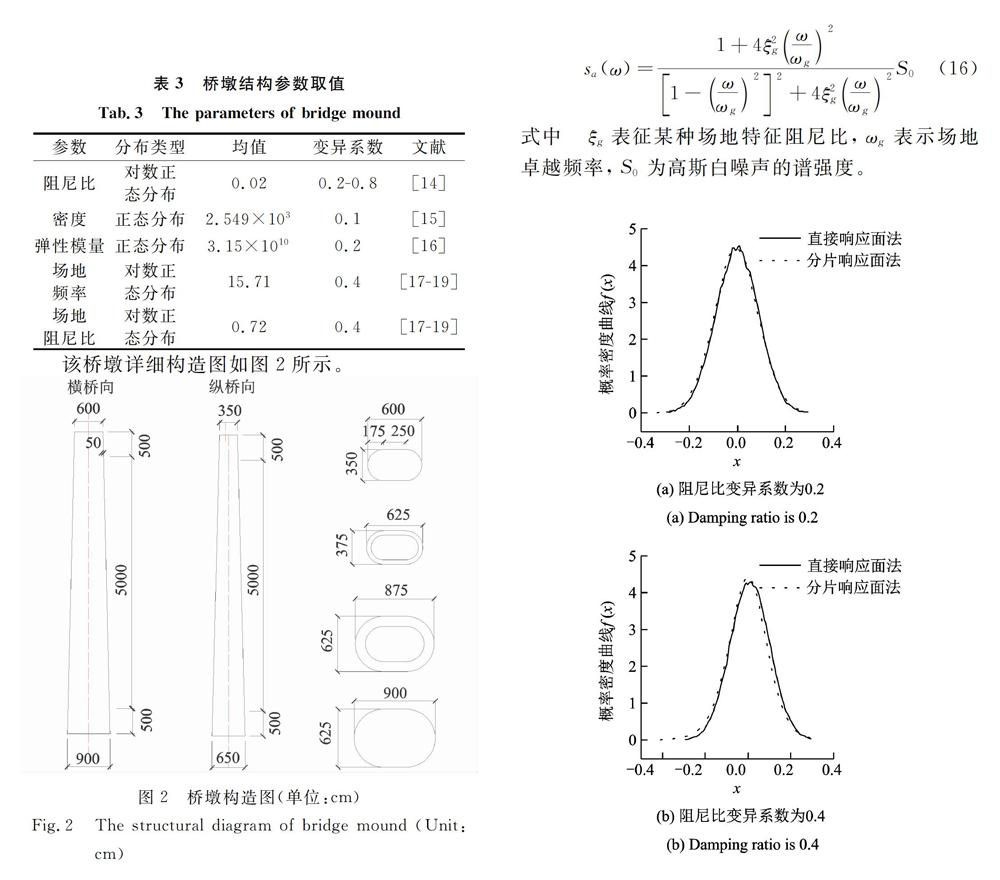
计算所用的桥墩是某铁路特大桥梁的混凝土桥墩,该桥墩高度为60m,桥墩采用变截面,顶端5m采用实心截面;底端5m采用实心截面,截面面积(9×6.5)m2;中问采用空心截面,壁厚从0.5m变化到1.2m。该桥墩采用C30混凝土材料,场地类型按Ⅱ类场地计算,地震强度So=0.01m2/s,具体结构参数如表3所示。
3.2不同阻尼比变异系数对桥墩在地震随机振动下响应的影响
对该桥墩的阻尼比变异系数取0.2-0.8进行研究,其他参数选取如表4所示。地震的加速度功率谱采用日本学者Kanai和Tajimi建议的过滤白噪声模型,即
分片响应面的区问划分规律依然采用表2划分的结果,将阻尼比划分子区问与其余随机变量相结合,带人桥墩模型中进行随机地震动分析,结构响应的标准差如表4所示,结构响应的概率密度曲线比较如图3所示。
从表4分析得知,在地震随机振动的激励下,随着结构阻尼比变异系数的增大,结构响应方差也明显呈增大趋势。而阻尼比的大变异性导致了响应面的极度不光滑,以致采用直接响应面法拟合响应方差呈现明显偏差;采用分片响应面法时,根据阻尼比变异系数划分响应面,尽可能精确模拟结构响应标准差,从结果看,结构响应的标准差也是平滑增大。
从图3可以看出,在地震随机振动的激励下,当阻尼比变异系数较小时,采用直接响应面法与分片响应面法拟合吻合较好,随着阻尼比的变异系数增大,两种方法吻合偏差逐渐增大,尤其当阻尼比变异系数达到0.8的时候,吻合偏差无法满足工程精度要求,因此分片响应面法在具体工程中具有实际工程意义。
4结论
(1)结构参数随机性对结构响应影响较大,例如阻尼比变异系数取0.8时,考虑结构随机性进行结构响应标准差分析,比不考虑结构随机性分析增大28.66%。而实际结构参数由于多种因素必然存在随机性,因此研究结构参数随机性对结构随机振动的影响具有一定的工程实际意义。
(2)提出了一种分片响应面方法,该方法旨在对变异系数较大的随机变量进行区问划分,并根据该参数取值大小在计算所得的子区问响应面上进行近似插值。该方法不但具有响应面法的连续性,而且能够在较大范围内对结构响应进行近似模拟,并且计算简单、准确。计算结果表明,分片响应面法能够满足工程精度的要求。
(3)阻尼比變异系数对桥墩结构在地震随机激励下的结构响应影响较大,采用分片响应面法可以很好地解决大阻尼比变异系数对结构随机振动的影响。

