齿轮图冠的优美性*
刘育兴,李淑萍,彭慧彦
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
1 引言
1963年,G.Ringel在文献[1]中提出了一个猜想:完备图K2n+1能够被分解成2n+1个子图,这些子图都与一个给定的有n条的树同构.这一猜想被称为Ringel猜想. 1966年,A.Rosa在文献[2]中在证明Ringel猜想的过程中,引入了β值这一工具,1972年,S.W.Golomb在文献[3]中把β值称为优美标号,并一直沿用至今.
在文献[2]中A.Rosa首次提出猜想:所有的树都是优美树.这就是著名的优美树猜想.这一猜想起初是与Ringel猜想有密切的联系而受到人们的关注, 然而由于它自身的原因, 不久就成为一个非常著名的猜想. 这个猜想至今没有被证明或否定.
虽然具有一定规则结构的许多图类都是优美图,但是V.N.Bhat-Nayak与S.K.Gokhale在[4]中证明了有无穷多类图不是优美图,并且在文献[2]中A.Rosa证明了:如果每一个顶点的度都是偶数且边数同余于1或2(模4), 则这个图一定不是优美图.特别地,圈C4n+1和C4n+2都不是优美图.
图的标号问题是组合数学中一个热门课题.它不仅属于图论领域,也属于设计理论的范畴. 图的优美标号是图的标号问题中的一种,有着广泛的应用.图的优美标号主要应用于编码设计、变压器箱设计、射电天文学、晶体结构中原子位置的测定和导弹控制码的设计等方面.研究图的优美性,即寻找图的优美标号.优美图是图论中极有趣的研究课题之一.
由于优美图的趣味性和应用性,自1972年S.W.Golomb明确给出优美图的定义以来,很快得到了人们的重视,获得了不少研究成果[1-7].
尽管在许多研究者的不懈努力下已经取得了丰硕的成果,但是对于图的优美性的研究仍有大量的工作要做,已经证明判定任意一个图是否为优美图是一个NP-困难问题,即对于给定的一个图,判定它是否为优美图,不存在一个有效算法. 因此,对于图的优美性的研究还有很长的路要走.
2 定义及定理
文中所讨论的图G(V,E)都是简单无向图.V(G)和E(G)分别表示G的顶点集和边集.|E(G)|(或|E|)表示图G的边数,N+是正整数集合.文中未说明的符号及术语均同于文献[1].
定义1[1]对于一个图G(V,E),若存在单射f:V(G)→{0,1,2,…,|E|-1},使得导出映射f′(uv)=|f(u)-f(v)|是E(G)→{1,2,3,…,|E|-1}的双射,则称G为优美图,而f称为G的一个优美标号.
定义2[1]由圈Cn的每个顶点都与同一个不在Cn上的顶点相连接所得到的图,叫做轮,记作Wn.

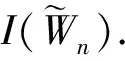
文献[2]中马克杰和冯成进已经证明了下述定理.


3 定理1的证明
下面证明定理1,我们根据n的取值分以下3种情形进行讨论.


图1 三个特殊齿轮图的冠的优美标号


图2 齿轮图的冠
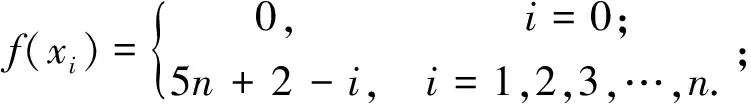



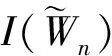



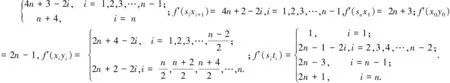
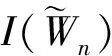


图3 两个特殊齿轮图的冠的优美标号

