考虑颗粒破碎特性的机场高填方变形与稳定性分析

单军杰 刘汉龙 肖杨 尹振宇 杨忠平 姚仰平

摘 要： 近年来，中国西南山区的机场高填方建设进入快速发展阶段，具有良好工程特性的堆石料等粗粒土广泛应用于高填方。机场高填方内部应力较高，粗粒土等填筑材料会产生颗粒破碎，分析颗粒破碎特性对高填方变形和稳定性的影响具有重大工程意义。使用离散元颗粒流法对高填方建立数值模型，采用强度折减法模拟了高填方的变形演化过程，利用Russell和Muir Wood颗粒破碎准则，对颗粒破碎和颗粒不破碎两种情况分别进行了离散元的数值模拟分析，对比研究了考虑颗粒破碎对高填方变形和稳定性的影响。研究结果表明：粗粒土颗粒破碎后产生的小颗粒将滑移充填颗粒间的空隙，使高填方变形量增加，高填方土体的抗剪强度降低，进而使高填方的安全系数降低，严重影响高填方的稳定性。

关键词： 高填方;颗粒破碎;离散元;变形;稳定性

中图分类号：TU433   文献标志码：A   文章编号：2096-6717（2020）02-0017-06

Deformation and stability analysis of airport high coarse-granular fills considering particle breakage characteristics

Shan Junjie1， Liu Hanlong1， Xiao Yang1， Yin Zhenyu2， Yang Zhongping1， Yao Yangping3

（1.School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China; 2.Department of Civil and Environmental Engineering， Hong Kong Polytechnic University， Hong Kong， P. R. China; 3.School of Transportation Science and Engineering， Beihang University， Beijing 100191， P. R. China）

Abstract： In recent years， the airport high coarse-granular fill construction in the southwest mountain area of China has entered a stage of rapid development， and coarse-grained soils such as rockfill materials with comparatively good engineering characteristics are widely used in high coarse-granular fill. The internal stress of high coarse-granular fill is large， and coarse-grained soil will cause particle breakage. It is of great engineering significance to analyze the impact of particle breakage characteristics on the deformation and stability of high coarse-granular fill. Modeling high coarse-granular fills using discrete element particle flow method. The deformation evolution process of the high coarse-granular fill is simulated through the strength reduction method. Based on the Russell & Muir Wood particle breakage criterion， two cases of particle breakage and dont breakage were simulated and analyzed respectively. In addition， we also focus on the effect of particle fragmentation on the deformation and stability of the high coarse-granular fill. DEM modelling results indicate that the small-size grains abraded from the host coarse-granular grains will slip and fill the gaps among the host grains， leading to an increase in deformation and a decrease in the shear strength， and further resulting in a decrease in safety factor and stability of high coarse-granular fill.

Keywords： high coarse-granular fill; particle breakage; discrete element; deformation; stability

近年来，伴随中国基础设施建设和西部大开发战略，中国西南山区的机场高填方及高土石坝建设进入快速发展阶段[1-3]。由于山区地形、地质条件复杂，经常需要进行高填方施工，具有良好工程特性的堆石料等粗粒土得到了广泛应用。与一般土体相比，粗粒土具有粒径大、颗粒破碎明显等特征[4]。由于高填方内部应力较高，粗粒土产生颗粒破碎将对填筑体的变形、稳定性都有很大影響[5]。所以，考虑粗粒土颗粒破碎对高填方的变形及稳定性研究有重大意义。

学者们对粗粒土的颗粒破碎特性进行了大量理论分析[6-9]和室内试验研究[10-13]。Xiao等[6]研究发现了粗粒土破碎临界状态线（BCSL）的位置与相对破碎有关，并提出了考虑颗粒破碎的粗粒土弹塑性模型。黄茂松等[8]重点研究了颗粒破碎的度量方法，发现了颗粒破碎对粗粒土剪胀性、临界状态线的影响以及相应的本构模型。刘汉龙等[12]

利用室内大型三轴试验对堆石等粗粒料的颗粒破碎进行了研究，发现颗粒破碎的增加将导致粗粒料抗剪强度的降低。丁艳辉等[13]通过常规三轴试验重点研究了堆石料遇水发生颗粒破碎造成高填方湿化变形的过程、特性及发生机制。

然而，受测量手段的限制，室内试验无法实时监测、量化试验过程中的粗粒土颗粒破碎现象。在数值模拟方面，目前有极限平衡法、有限元分析法等方法可以进行边坡的变形和稳定性分析[14]，但由于极限平衡法需要提前假定滑裂面的形状和位置，这些假定和简化可能与实际不符，且有限单元法无法动态模拟土坡的整个破坏过程。作为离散单元法之一的颗粒流方法，就可以很好地弥补上述方法所存在的弊端[15]。

笔者采用PFC2D软件，通过强度折减法[16]来模拟重庆某机场高填方的变形演化过程，并对比研究考虑颗粒破碎对高填方变形和稳定性的影响。

1 离散元模型与试验方案

1.1 模型生成及参数选取

采用 PFC2D软件，生成高为100 m、宽为170 m的高填方颗粒流模型。填筑材料采用直径为500 mm均一粒径的颗粒，试样初始孔隙率为0.1，高填方模型在自身重力的影响下完全處于稳定状态。模型中颗粒初始总数为20 973个。模型由一道水平墙和两道左右墙组成其边界条件，阻止了范围边缘颗粒的逸出，墙体摩擦系数为0.5。

模型的细观力学参数需要通过与室内试验对比调参获得。首先依据《土工试验方法标准》（GB/T 50123—1999）中的试验方法，通过室内试验获得所需的粗粒土宏观参数。室内试验主要包括粗粒土含水率试验、击实试验、直剪试验等。所得到的高填方宏观力学参数见表1。其宏观力学参数均满足已有资料标准。

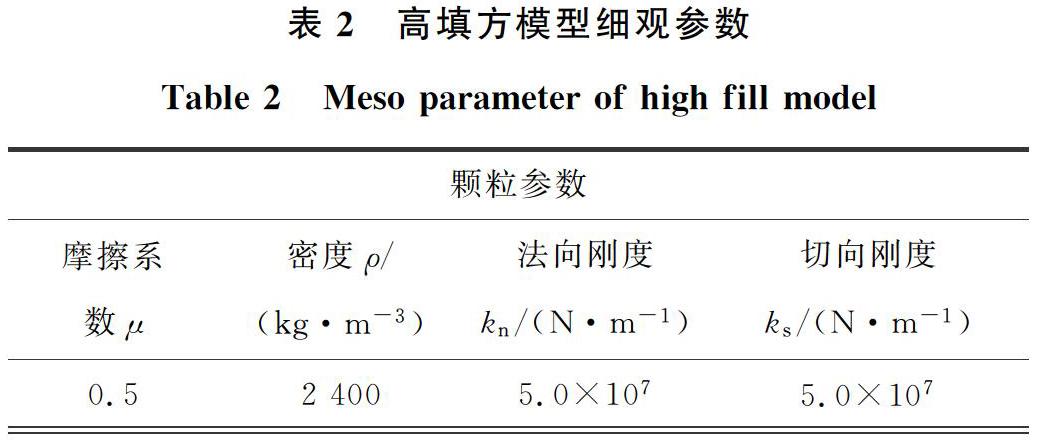
通过模拟双轴试验[17]，结合室内试验得到粗粒土宏观力学参数，采用试错法对颗粒细观参数进行标定，即对细观参数进行逐步调整并反复调参校对，得到与宏观参数匹配的模型细观力学参数[18]。得到的高填方模型细观力学参数见表2。

1.2 强度折减法基本原理

在边坡工程稳定性分析中，人们最关心的是边坡是否稳定，整体稳定的安全系数有多大。Duncan[16]指出，边坡安全系数可以定义为使边坡刚好达到临界破坏状态时对土体的剪切强度进行折减的程度。整个离散系统稳定与否的关键因素由摩擦系数μ和粘结强度pb决定。

强度折减法进行颗粒流模拟是把粘结强度pb与摩擦系数μ一同折减，直到整个高填方颗粒流模型达到其临界破坏状态时，这个折减系数则为该模拟模型的安全系数。所以，安全系数可定义为

Fs= pb pb′ = μ μ′  （1）

式中：pb′为折减后的边坡模型到达临界破坏状态的颗粒间粘结强度;μ′为折减后的边坡模型到达临界破坏状态的颗粒间摩擦系数。

1.3 颗粒破碎准则

真实破碎的物理过程是外界条件变化导致大颗粒变成小颗粒的过程。实际上，破碎准则是一个阀值条件，当颗粒的受力状态超过该条件时，将发生破碎。局部应力集中是导致颗粒破碎的重要因素，笔者采用Russell & Muir Wood[19]破碎准则，在线性接触模型下该准则可以表示为

Flim≤σlim，0  d d0  -3/m π 4 d2sin2θ0 （2）

式中：Flim为颗粒的极限强度;σlim，0为粒径为d0时颗粒的平均极限强度;θ0为力的作用范围的圆心角，取π/9;m为Weibull模量，随强度提高而减小，取2。

较普遍使用的Mohr-Coulomb准则是基于整个颗粒受到的平均应力，不能体现出颗粒间接触力的应力集中现象;而现实中的破碎是颗粒在应力集中处开始产生裂纹从而引起破碎。因此，Mohr-Coulomb理论破碎准则并不能真实反映颗粒的破碎情况。而Russell & Muir Wood破碎准则是基于颗粒受集中荷载推导而来，更能反映颗粒在接触力作用下的应力集中现象。高填方模型中颗粒的破碎过程如图1所示。

由图1可知，当颗粒的受力状态超过破碎标准时会发生破碎，生成一个稍小的颗粒及很多小颗粒，之后破碎产生的小颗粒会填充到颗粒间的空隙中，如图1所示红色颗粒的破碎过程。

1.4 试验方案

用离散元颗粒流法建立高填方模型，检测到有颗粒发生破碎后，将试样状态保存。改变颗粒接触模型使颗粒完全弹开，记录新生成无重叠颗粒的位置，再将之前保存的试样重新载入。删除破碎颗粒，将新生成的无重叠颗粒放入新试样中继续运行。

将强度折减法原理引入到高填方模型的分析中，通过不断增大强度折减系数，对比研究所建立的高填方模型在颗粒破碎和未破碎情况下的稳定性差异，得到高填方模型在颗粒破碎与未破碎情况下的安全系数。

之后，模型选取同一强度折减系数，在高填方模型整体稳定的情况下，对比研究高填方模型在颗粒破碎与未破碎情况下的变形差异，主要包括高填方潜在滑移面的形状和位置、累计最大位移等变形信息。

1.5 高填方破坏的判据

如何判定高填方模型是否达到了临界破坏状态，是用数值分析方法研究高填方稳定性的难题。本离散元模型计算中把收敛容许值设为10-5，当计算不收敛时，延长迭代步数以便更好地观察高填方模型的变形情况。离散元法采用位移分析方法，每个时步下都会发生位移，因此，高填方破坏的判定依据宜选取临界位移指标。本高填方模型离散元计算中，在累计最大位移达到3 m以上时，计算不收敛，高填方发生明显破坏，且土体变形仍在持续。故使用高填方土体失稳的累计最大位移达到3 m以上且计算不收敛作为界定高填方破坏的依据。

2 模拟结果分析

2.1 高填方稳定性对比分析

对所建立的高填方模型采用强度折减法计算其安全系数。首先要确保高填方在初始状态时处于稳定状态，即初始的强度折减系数取1，分别分析高填方模型在颗粒不破碎和破碎情况下的稳定性。模拟结果如图2所示（图2中云图为高填方模型中颗粒的位移云图，单位为m）。由图2可知，高填方模型在初始时均处于稳定状态。

逐渐增大强度折减系数至高填方模型失稳破坏。在颗粒未破碎的情况下，当强度折减系数增大至1.4时，高填方整体性良好，坡顶无裂纹，坡面未出现较大滑移，高填方土体累计最大位移为2.38 m，出现潜在滑移面，但计算收敛，说明此时高填方还未破坏，并处于稳定状态。当折减系数增大至1.5时，坡面出现明显滑移面，坡顶土体下沉，计算不收敛。高填方土体失稳的累计位移达到19.1 m，且延长迭代步数时，坡面土体位移变化明显，说明此时高填方已失稳破坏。所以，在颗粒未发生破坏时，高填方模型的安全系数为1.4。颗粒未破碎时高填方模型稳定性结果如图3所示（图3中云图为高填方模型中颗粒的位移云图，单位为m）。

在颗粒破碎的情况下，当强度折减系数增大至1.3时，高填方整体性良好，坡顶无裂纹，坡面未出现较大滑移，高填方土体累计最大位移为2.52 m，出现潜在滑移面，但计算收敛，说明此时高填方还未破坏，并处于稳定状态。当折减系数增大至1.4时，坡面出现明显滑移面，坡顶土体下沉，计算不收敛。高填方土体失稳的累计位移达到26.3 m，且延长迭代步数时，坡面土体位移变化明显。说明此时高填方已失稳破坏。所以，在颗粒发生破坏时，高填方模型的安全系数为1.3。颗粒破碎时高填方模型稳定性结果如图4所示（图4中云图为高填方模型中颗粒的位移云图，单位为m）。

通过对比分析可知，颗粒未破碎时高填方模型的安全系数为1.4，颗粒破碎时高填方模型的安全系数为1.3。说明颗粒破碎对高填方的稳定性有较大的不利影响。在强震和高应力作用下，粗粒土更易导致颗粒破碎而削弱粗粒土的强度，会严重影响高填方的安全性及稳定性。

2.2 高填方变形对比分析

高填方模型在选取同一强度折减系数且处于整体稳定状态时，对比研究模型在颗粒破碎与未破碎情况下的变形差异，选取强度折减系数为1.3。主要对比分析高填方潜在滑移面的形状和位置、土体累计最大位移等变形信息。变形对比如图5所示（图5中云图为高填方模型中颗粒的位移云图，单位为m）。

由图5可知，在强度折减系数为1.3时，高填方模型均未发生大变形破坏。但相对于颗粒不发生破碎的情况，在颗粒发生破碎的情况下，高填方模型的潜在滑移面埋深更大，约30 m，且潜在滑移面坡度更大。在颗粒破碎时，高填方的土体累计最大位移为2.52 m;而颗粒不破碎时，高填方的土体累计最大位移仅为1.4 m。通过对比可知，颗粒破碎对高填方的变形有不利影响，会增加高填方的变形破坏程度。

2.3 颗粒破碎影响机理探究

高填方模型的颗粒破碎细节如图6所示。（图6中红色颗粒为破碎后的颗粒）。

由图6可知，高填方应力较大的区域主要集中在高填方内部，这些区域的土体最先发生颗粒破碎。结合图1可知，颗粒破碎后的小颗粒会滑移充填颗粒间空隙，使高填方的变形量增加，且土体抗剪强度产生一定程度的削弱。结合图4可知，随着颗粒破碎的增加，粗粒料的抗剪强度会降低，导致高填方的变形增加，严重影响高填方的安全性及稳定性。

3 结论

采用离散元颗粒流法对高填方建立模型，利用强度折减法模拟了高填方的变形演化过程，并对比研究了考虑颗粒破碎对高填方变形和稳定性的影响。得到以下主要结论：

1）Russell等[19]提出的破碎准则可以作为球形颗粒的破碎准则，并很好地应用于离散元中，能反映颗粒的真实受荷破碎情况。

2）结合离散元颗粒流模拟，探究了颗粒破碎机理。颗粒破碎后小颗粒会滑移充填颗粒间空隙，使高填方的变形量增加，土体的抗剪强度产生一定程度的削弱。

3）动态模拟了高填方的整个破坏过程，颗粒破碎使高填方的潜在滑移面埋深更大、坡度更大，颗粒破碎会增加高填方的变形破坏程度。

4）定量给出了高填方的安全系數，证明颗粒破碎会降低高填方的安全性及稳定性。该离散元颗粒流模型具有普适性，对实际高填方工程具有重要指导意义。

参考文献：

[1]    杨校辉， 朱彦鹏， 周勇， 等. 山区机场高填方边坡滑移过程时空监测与稳定性分析[J]. 岩石力学与工程学报， 2016， 35（Sup2）：3977-3990.

YANG X H， ZHU Y P， ZHOU Y， et al. Time-space monitoring and stability analysis of high fill slope slip process at a airport in mountain region [J]. Chinese Journal of Rock Mechanics and Engineering， 2016， 35（Sup2）：3977-3990. （in Chinese）

[2]   杨忠平， 李万坤， 胡元鑫， 等. 压实系数对粗粒土剪切特性的影响[J]. 地下空间与工程学报， 2017， 13（2）：348-356.

YANG Z P， LI W K， HU Y X， et al.Effect of compaction coefficient on shear characteristics of coarse grained soil [J]. Chinese Journal of Underground Space and Engineering， 2017， 13（2）：348-356. （in Chinese）

[3]   雷晓丹， 杨忠平， 张晓景， 等. 土石混合料剪切特性及块石破碎特征[J]. 岩土力学， 2018， 39（3）：899-908， 916.

LEI X D， YANG Z P， ZHANG X J， et al. Shear properties and rock block breakage characteristics of soil-rock mixtures [J]. Rock and Soil Mechanics， 2018， 39（3）：899-908， 916. （in Chinese）

[4]   姚仰平， 黄冠， 王乃东， 等. 堆石料的应力 应变特性及其三维破碎本构模型[J]. 工业建筑， 2011， 41（9）：12-17， 104.

YAO Y P， HUANG G， WANG N D， et al. Stress-strain characteristic and three-dimensional constitutive model of rockfill considering crushing [J]. Industrial Construction， 2011， 41（9）：12-17， 104. （in Chinese）

[5]   梁军， 刘汉龙， 高玉峰. 堆石蠕变机理分析与颗粒破碎特性研究[J]. 岩土力学， 2003， 24（3）：479-483.

LIANG J， LIU H L， GAO Y F. Creep mechanism and breakage behaviour of rockfill [J]. Rock and Soil Mechanics， 2003， 24（3）：479-483. （in Chinese）

[6]    XIAO Y， LIU H L. Elastoplastic constitutive model for rockfill materials considering particle breakage [J]. International Journal of Geomechanics， 2017， 17（1）：04016041.

[7]    MING H， SUN K， XU X， et al. A hypoplastic constitutive model for rockfill materials considering the influence of particle breakage on representative void ratio [J]. Rock and Soil Mechanics， 2016， 37（1）：33-U577.

[8]   黄茂松， 姚仰平， 尹振宇， 等. 土的基本特性及本构关系与强度理论[J]. 土木工程学报， 2016， 49（7）：9-35.

HUANG M S， YAO Y P， YIN Z Y， et al. An overview on elementary mechanical behaviors， constitutive modeling and failure criterion of soils [J]. China Civil Engineering Journal， 2016， 49（7）：9-35. （in Chinese）

[9]   蔡正银， 李小梅， 关云飞， 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报， 2016， 38（5）：923-929.

CAI Z Y， LI X M， GUAN Y F， et al. Particle breakage rules of rockfill materials [J]. Chinese Journal of Geotechnical Engineering， 2016， 38（5）：923-929. （in Chinese）

[10]     XIAO Y， LIU H L， DESAI C S， et al. Effect of intermediate principal-stress ratio on particle breakage of rockfill material [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2016， 142（4）：06015017.

[11]    XIAO Y， LIU H L， DING X M， et al. Influence of particle breakage on critical state line of rockfill material [J]. International Journal of Geomechanics， 2016， 16（1）：04015031.

[12]   劉汉龙， 秦红玉， 高玉峰， 等. 堆石粗粒料颗粒破碎试验研究[J]. 岩土力学， 2005， 26（4）：562-566.

LIU H L， QIN H Y， GAO Y F， et al. Experimental study on particle breakage of rockfill and coarse aggregates [J]. Rock and Soil Mechanics， 2005， 26（4）：562-566. （in Chinese）

[13]   丁艳辉， 张丙印， 钱晓翔， 等. 堆石料湿化变形特性试验研究[J]. 岩土力学， 2019， 40（8）：2975-2981， 2988.

DING Y H， ZHANG B Y， QIAN X X， et al. Experimental study of the characteristics of wetting deformation of rockfill materials [J]. Rock and Soil Mechanics， 2019， 40（8）：2975-2981， 2988. （in Chinese）

[14]   李典庆， 肖特， 曹子君， 等. 基于极限平衡法和有限元法的边坡协同式可靠度分析[J]. 岩土工程学报， 2016， 38（6）：1004-1013.

LI D Q， XIAO T， CAO Z J， et al. Auxiliary slope reliability analysis using limit equilibrium method and finite element method [J]. Chinese Journal of Geotechnical Engineering， 2016， 38（6）：1004-1013. （in Chinese）

[15]   韩洪兴， 陈伟， 邱子锋， 等. 考虑破碎的堆石料二维颗粒流数值模拟[J]. 岩土工程学报， 2016， 38（Sup2）：234-239.

HAN H X， CHEN W， QIU Z F， et al. Numerical simulation of two-dimensional particle flow in broken rockfill materials [J]. Chinese Journal of Geotechnical Engineering， 2016， 38（Sup2）：234-239. （in Chinese）

[16]    DUNCAN J M. State of the art：limit equilibrium and finite-element analysis of slopes [J]. Journal of Geotechnical Engineering， 1996， 122（7）：577-596.

[17]   焦玉勇， 王浩， 马江锋. 土石混合体力学特性的颗粒离散元双轴试验模拟研究[J]. 岩石力学与工程学报， 2015， 34（Sup1）：3564-3573.

JIAO Y Y， WANG H， MA J F. Research on biaxial test of mechanical characteristics on soil-rock aggregate（SRA） based on particle flow code simulation [J]. Chinese Journal of Rock Mechanics and Engineering， 2015， 34（Sup1）：3564-3573. （in Chinese）

[18]   楊忠平， 雷晓丹， 王雷， 等. 含石量对土石混合体剪切特性影响的颗粒离散元数值研究[J]. 工程地质学报， 2017， 25（4）：1035-1045.

YANG Z P， LEI X D， WANG L， et al. Impact of stone content to shear properties of soil-rock mixture using particle flow code simulation [J]. Journal of Engineering Geology， 2017， 25（4）：1035-1045. （in Chinese）

[19]    RUSSELL A R， MUIR WOOD D. Point load tests and strength measurements for brittle spheres [J]. International Journal of Rock Mechanics and Mining Sciences， 2009， 46（2）：272-280.

（编辑 胡英奎）

收稿日期：2019-12-01

基金项目：  国家自然科学基金（41831282、51922024、51578096）

作者简介：  单军杰（1992- ），主要从事颗粒破碎研究，E-mail：shanjunjie19@163.com。

肖杨（通信作者），教授，博士生导师，E-mail：hhuxyanson@163.com。

Received： 2019-12-01

Foundation items：  National Natural Science Foundation of China （No. 41831282， 51922024， 51578096）

Author brief：  Shan Junjie（1992- ）， main research interest： particle breakage， E-mail：shanjunjie19@163.com.

Xiao Yang（corresponding author）， professor， doctorial supervisor， E-mail：hhuxyanson@163.com.