E2地震作用下某连续梁桥抗震性能分析
时小梅
(鲁南高速铁路有限公司,山东 济南 250102)
桥梁作为跨越障碍物的建筑物,在人类社会经济发展和日常生活中发挥着巨大的作用,连续梁桥由于施工简单、能够装配式作业等特点,在桥梁建设中得到了广泛的应用。我国由于地处亚欧板块与太平洋板块之间,近年来地震频发,造成了大量桥梁毁坏甚至倒塌,不仅导致巨大的经济损失,而且给救援工作带来了不便[1],因此开展连续梁桥的抗震性能研究具有重要的意义。
目前,国内外学者针对连续梁桥的抗震开展了诸多研究。文献[2]基于地震易损性通过设置不同的减震措施对连续梁桥的减隔震措施进行了研究,指出高烈度地区连续梁须通过减隔震设计达到抗震设防要求。文献[3]通过输入E2水平的强震,对城市连续梁桥双柱墩墩顶容许位移进行了分析计算,阐述了计算方法和流程。文献[4]以某大跨长联波形钢腹板连续梁桥为工程背景,对其隔震设计进行了研究,得出采用速度锁定器+摩擦摆支座复合抗震的措施可有效改善结构受力。文献[5]以干海子特大桥为工程背景,设置不同的结构设计参数工况,研究了钢管混凝土格构式高墩连续梁桥的抗震设计,研究结果表明合理的结构参数设置可以有效降低结构地震响应。文献[6]研究了某4跨连续梁桥铅芯橡胶支座减隔震的分析方法,考虑结果误差,设计时建议对规则桥梁简化分析结果乘以1.1的安全系数。以上有关连续梁地震响应的研究,大多集中于减隔震措施及参数设置方面,但均未涉及连续梁桥自身的抗震性能研究。
本文以某(3×25 m)装配式预应力混凝土箱型连续梁桥为工程背景,建立全桥MIDAS CIVIL有限元模型,输入E2水平下的3条地震动,通过动态时程分析方法从强度角度分析了该连续梁桥的抗震性能,并对本桥抗震性能做出评估。
1 工程概况及有限元模型建立
1.1 工程概况
某装配式预应力混凝土箱型连续梁桥(见图1),跨径布置为3×25 m,主梁采用箱型截面。该桥箱梁采用C50混凝土,盖梁、墩柱采用C35混凝土,桩基采用C30混凝土。边墩桩长50 m,桩基为直径1.3 m的圆形截面;中墩桩长60 m,桩基为直径1.5 m的圆形截面;中墩为直径1.2 m的圆形截面。该桥按照延性构件进行设计,抗震设防烈度为7度,设计基本地震加速度值为0.15g,抗震措施按抗震设防烈度8度设计。
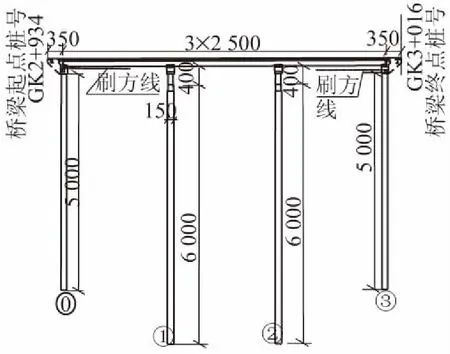
图1 某装配式预应力混凝土箱型连续梁桥立面图(单位:cm)
1.2 建立有限元模型
采用MIDAS对某(3×25 m)装配式预应力混凝土箱型连续梁桥建立有限元分析模型。全桥由350个节点和325个单元组成,箱梁、盖梁、墩柱、桩基均采用空间梁单元模拟,二期恒载为160 kN/m,桩底采用一般支撑,约束其平动自由度和转动自由度,对于桩土之间的作用采用弹簧来模拟,弹簧的刚度按“m”法计算[7],左边墩与主梁间模拟固定支座连接,其与墩梁间模拟活动支座连接。有限元模型见图2。
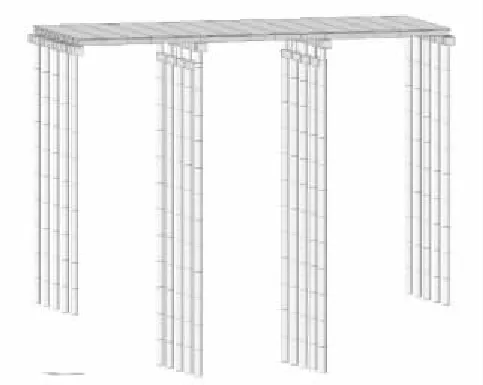
图2 有限元分析模型
2 动力特性分析
表1中给出了模型前5阶的动力特性。根据结构相关抗震规范可知,结构的自振周期与其自身的刚度成反比,从延性角度进行抗震设计时,较大的自振周期在一定范围内有助于减弱地震响应。另外,结构自振周期是决定地震影响系数的重要因素,在相同的震级和场地条件下,当结构自振周期与场地的特征周期越接近则水平地震影响系数越大。

表1 连续梁桥动力特性
3 地震动输入
依据《公路桥梁抗震设计细则(JTG/TB02-01-2008)》并结合桥梁类型、桥址处场地土特性及地震设防要求,本连续梁桥为B类桥梁,场地土属于Ⅱ类场地,按照8度抗震设防烈度要求,本文选用安评报告中E2水平下3条地震波,所选地震波加速度分别为0.23g、0.21g及0.24g。地震动按照(顺+竖)的方式输入,竖向加速度按照水平向的65%取值。图3~图5为所选地震动加速度时程曲线。

图3 第1条安评地震动 图4 第2条安评地震 图5 第3条安评地震动
4 抗震性能分析
4.1 地震响应结果
恒载单独作用下的内力见表2,E2地震作用下的恒载与地震作用组合列于表3,地震作用下的内力取3条地震波作用下的最大值。表中内力组合为恒载内力和地震作用之和,最大轴力为地震轴力与恒载轴力之和,最小轴力为两者之差。
由表3可知,在恒载和E2地震作用下, 通过对比可知,在(顺+竖)方式输入下,无论是最大轴力还是最小轴力,中墩均大于边墩,故中墩为最大轴力墩;从面内角度分析,最大弯矩和剪力均出现在边墩,边墩为最大受力墩;从面外角度分析,最大弯矩和剪力均出现在中墩,中墩为最大受力墩;由地震响应结果可以看出,顺桥向地震响应远大于横桥向地震响应,设计时顺桥向起控制作用。

表2 恒载的内力
注:面内指桥梁立面所在平面,面外指桥梁横截面所在平面,下同。
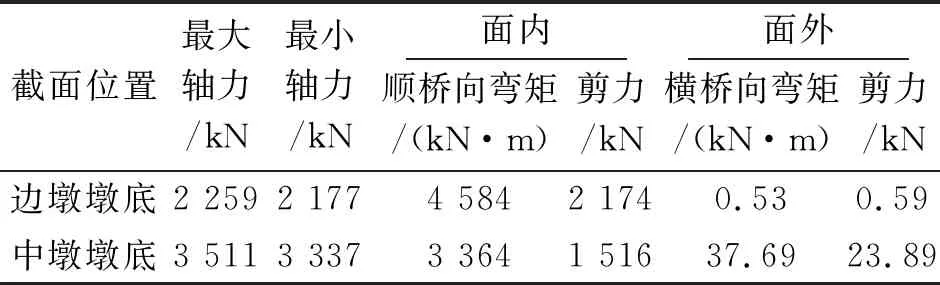
表3 E2地震作用与恒载的内力组合
4.2 抗震性能分析
本节应用UCfyber弯矩曲率计算软件分析了墩底截面的屈服弯矩,控制截面的屈服弯矩列于表4,其中,MyP表示顺桥向屈服弯矩,MzP表示横桥向屈服弯矩,由于控制截面均为圆形截面,所以顺桥向屈服弯矩与横桥向屈服弯矩相同。
由表4可知,最大轴力作用下,边墩墩底顺桥向和横桥向屈服弯矩均为5 035 kN·m,中墩墩底顺桥向和横桥向屈服弯矩均为4 069 kN·m;最小轴力作用下,边墩墩底顺桥向和横桥向屈服弯矩均为5 024 kN·m,中墩墩底顺桥向和横桥向屈服弯矩均为4 045 kN·m。本桥在E1地震作用下各构件均处在弹性状态,对比表2和表3可知,在恒载和E2地震作用下,本桥关键截面的最大弯矩小于其屈服弯矩,且具有一定的安全储备,可见本桥具有良好的抗震性能。

表4 顺桥向输入时控制截面的屈服弯矩
5 结论
(1)该连续梁桥自振周期较小,通过动力特性分析可知,其第一阶自振周期为2.562 s,振型为主梁横向弯曲振动。
(2)地震动在(顺+竖)方式输入下,顺桥向地震响应远大于横桥向地震响应,在设计中顺桥向起控制作用。
(3)在恒载和E2地震共同作用下,本桥边墩墩底弯矩和中墩墩底弯矩均小于其屈服弯矩,且有一定的安全储备;从强度角度分析,本桥抗震性能良好。

