类氢离子旋轨耦合及基于微扰理论的能级修正研究①

庞福荣， 韩海生， 张海丰

(佳木斯大学理学院，黑龙江 佳木斯 154007)

0 引 言

在对具体的量子力学体系的薛定谔方程进行求解时，由于体系的哈密顿算符比较复杂，往往难以求得精确的解，因此，量子力学中往往用近似解的方法来求解，其中有效的近似方法就是利用微扰理论，其在物理、化学、工程计算中都得到了广泛的应用[1-5]。

类氢离子模型就是只由一个原子核和一个电子组成的系统，其在很多方面得到了应用，对于该模型的处理往往采用中心立场[4-9].

自轨耦合即自旋轨道相互作用，它是微观粒子的自旋和轨道动量相互作用时导致的能级的“细小”分裂。本文将详细讨论类氢离子的旋轨耦合，并基于微扰理论对类氢离子能级进行修正.

1 类氢离子的旋轨耦合

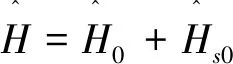
(1)

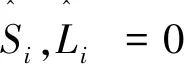
(2)

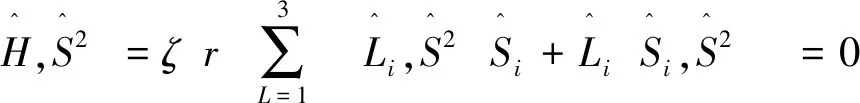
(3)

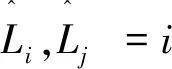
(4)

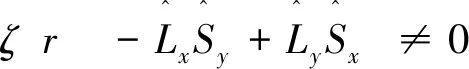
(5)

从(4)和(5)式可以得到得出

(6)

(7)

(8a)

(8b)

(9a)

(9b)

其中-JMJ。由(9)式给出的角向波函数满足

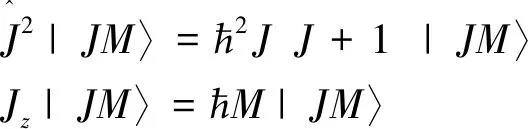
(10)

作为推论

(11)

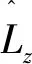
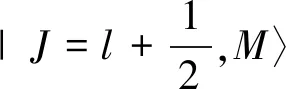
(12)

其中|M|

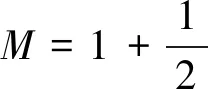
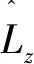
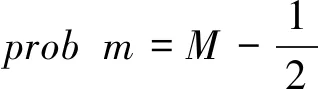
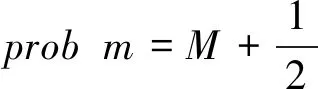
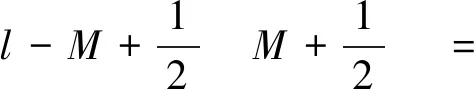
(13)

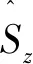
(14)

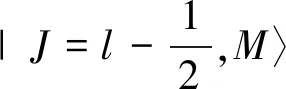
(15)

其中m和的平均值为

(16)

2 利用微扰理论讨论类氢离子旋轨耦合引起的能级修正

(17)

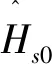
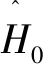
(18)

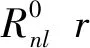
对于l≠0时，得到

(19)

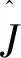
利用一阶微扰论

(20)

(21)

再应用式(19)，可以得到

(22)

(23)

每个能级都是2J+1重简并的，在磁场下这个简并被解除。

最后求自旋-轨道耦合引起的能级修正。自旋-轨道耦合的一阶能级修正正比于径向积分ζnl，对于l≠0，可以得到

(24)

对〈r-3〉nl的计算给出

(25)

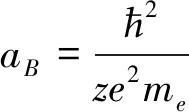
(26)

3 结 论