数字图像的二重分块置乱算法①

丁永胜, 张水胜

(齐齐哈尔大学理学院信息与计算科学系, 黑龙江 齐齐哈尔 161006)

0 引 言

图像信息一直是人类表达信息的重要手段。随着计算机科学技术的发展，数字图像逐渐成为信息表达和传播的主流方式之一，成为人们生活中不可或缺的部分。但图像信息的安全性问题日益受到人们的关注,譬如如何确保图像信息在存储和传播过程中的安全, 如何保证图像，文本等相关数字信息的版权等等。因此研究数字图像的加密和安全问题已成为当前数字图像处理领域研究的重要课题之一。数字图像置乱技术是图像信息加密与隐藏的一种方法，也是信息隐藏技术预处理工作之一。典型的图像置乱算法如：Fibonacci变换、Hilbert变换、生命游戏变换、幻方变换、Logistic变换、Gray码变换、异或变换及位平面变换等。人们在此基础上人不断取得了一系列成果[1-4]。基于仿射变换的二重分块置乱算法，其主要思想是，将待加密(置乱)图像进行二重分块操作，然后针对每一重中图像块矩阵进行位置置乱，并对每一重中图像块置乱后的图像进行像素置乱，从而得到加密图像。

1仿射变换

仿射变换的一般形式为

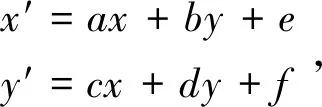
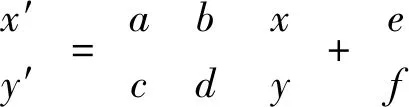
(1)

其中(x,y)为原始坐标，(x′,y′)为变换后的坐标。a，b，c，d，e，f分别为变换的参数系数。

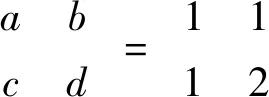
(2)

其中n为迭代(置乱)次数，N为图像矩阵阶数，(x,y)为原始图像像素位置，(x′,y′)为置乱后图像像素位置。利用 Arnold 变换置乱图像像素，使其变成看起来毫无意义图像，从而实现隐藏图像信息，迭代(置乱)次数作为密钥，从而增强了系统的保密性与安全性。

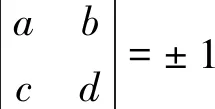
对于图像IN×N的二维变换形式如下：

(3)

该算法除了迭代(置乱)次数作为密钥外，参数a,b,c,d都可以作为密钥。进一步增强了系统的保密性与安全性[7-8]。

2 图像二重分块置乱

2.1 图像二重分块算法

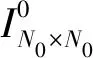
2.2 加密置乱与解密过程

加密置乱过程：

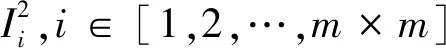
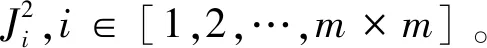
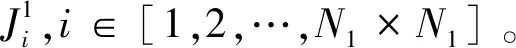
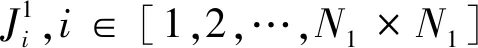
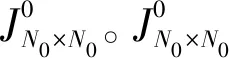
3 实验结果与分析

传统的仿射变换置乱，利用公式(3)将参数a，b，c，d以及置乱次数n作为密钥，密钥数量少，而且需要置乱多次才能达到理想效果。而且当迭代次数到一定数量时会恢复原图，加密安全性较低；而采用的二重分块置乱算法时，每次置乱的参数ai，bi，ci，di以及置乱次数ni作为密钥,密钥数量多，同时只要在较少的置乱次数下就能够达到理想的加密效果。大大提高了图像置乱加密的安全性。

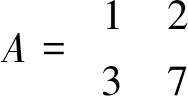
图1 原图像 图2 第一重块置乱图像 图3 第二重块像素置乱 图4 置乱图像

通常情况下，一幅图像的相邻像素之间具有很大相关性。但是对于置乱图像，相邻像素之间的相关性越小说明该图像置乱加密效果越好，因此可以利用相关系数来衡量图像置乱加密效果。

设有两个变量分别为x和y，Pearson相关系数的计算公式

(4)

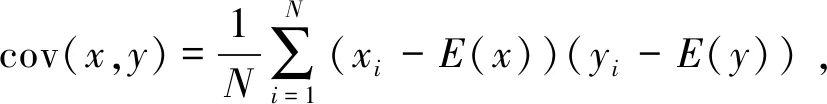
|rxy|<0.3，表示低度线性相关；

对图1到图4的图像进行测试，对整个图像的行、列相邻像素点(水平方向、垂直方向)计算相关系数，并对所有行、列相关系数的最大值进行比较。 图像加密前后邻域像素最大相关系数见表2。从表2看出原图像的像素相关性都非常高，而图4加密图像的相关性非常小(接近于0)，故算法具有很强的置乱效果和抗统计分析攻击能力。

表1 行、列相邻像素最大相关系数

4 结 论

利用仿射变换进行二重置乱数字图像。主要将图像连续两次分块并执行块置乱和像素置乱的二重操作。得到的图像置乱效果相对于传统的仿射变换，具有密钥数量大、置乱效果好、抗统计分析攻击能力强等特点。有效解决了传统二维仿射变换置乱效果较差、效率低等问题，通过理论分析和实验证明该算法是非常有效的。